线性代数
线性代数中的部分内容(待续)
1.逆矩阵
对给定矩阵A,若存在一个矩阵B,满足 AB = BA = I,则称矩阵A可逆,并称矩阵B是A的逆矩阵。
求A的逆阵的方法
[ A | I ] ~ [ I | B ] ----> B即是A的逆阵
2.初等变换
(1) 对调矩阵中的任意两行(列)
(2) 以非零常数乘以矩阵中的某一行(列)中的所有元素
(3) 把矩阵中的某一行(列)的所有元素的k倍(k是常数)加到另一行(列)的对应元素上去
如果把矩阵A经过有限次初等变换变成矩阵B,就称矩阵A与B等价,记作A ~ B。
3.矩阵A可逆的充要条件:
A可表示为有限个初等矩阵的乘积
4. 行列式
行列式按行(列)展开法则
行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和。
性质及其推论:
(1) 行列式与它的转置行列式相等.
(2) 行列式中如果有两行(列)元素成比例,则此行列式等于零(包括有0行(列)、两行(列)相等).
(3) 若行列式的某一行(列)的元素都可分成两数之和,则行列式可分成两个对应行列式的和.
(4) 初等变换得到的行列式值的变化
将方阵A中的某行(列)乘以k得到B,则|B| = k|A|
将方阵A中的某行(列)的k倍加到另一行(列)得到B,则|B| = |A|
交换方阵A中的任两行(列)得到B,则|B| = -|A|
(5) 设A B 均为n阶方阵,则A与B的乘积矩阵的行列式等于A的行列式与B的行列式的乘积.即|AB| = |A| |B|
5.伴随阵和逆矩阵
(1)n阶矩阵A,则AA^* = A^*A = |A|I
(2)|A^*| = |A|^n
(3)A^-1 = A^*/|A|
其中
| A11 A21 ... An1 |
| A12 A22 ... An2 |
| . . . . |
| . . . . | = A^*
| . . . . |
| A1n A2n ... Ann |
6. 齐次线性方程组和非齐次线性方程组
(1) n元齐次线性方程组A m*n x = 0有非零解的充要条件是其系数矩阵的秩r(A) < n,且其通解中带有n-r(A)个任意参数。(m*n是矩阵的m行n列。非零解称为非平凡解,零解称为平凡解)
(2) n元非齐次线性方程组 Ax=b有解的充要条件是系数矩阵A的秩等于增广矩阵[A | b]的秩。
r(A) = r(A|b) = n 方程组有唯一解
r(A) = r(A|b) < n 方程组有无限多个解,且其通式中带有n-r(A)个任意参数
r(A) != r(A|b) 方程组无解
(暂用A|b来表示增广阵)
7. 向量空间
(1)给定向量组 a1, a2, ..,an,若存在不全为零的数k1, k2,...,kn,使得
k1a1 + k2a2 + ... + knan = 0,则称向量组是线性相关的。当且仅当k1 = k2 = .. = kn = 0时才成立,则称向量组是线性无关的。
(2)给定向量组 a1, a2, ..,an 线性相关的充要条件是由它所构成的矩阵A[a1, a2,..,an]的秩小于n。线性无关的充要条件是向量的秩等于n。
8.特征值问题与二次型
三角阵的特征值即为主对角线上的元素



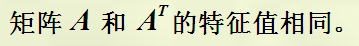
以下是对线性代数中用到的性质和一些求解(持续跟新)。
1.逆矩阵
对给定矩阵A,若存在一个矩阵B,满足 AB = BA = I,则称矩阵A可逆,并称矩阵B是A的逆矩阵。
求A的逆阵的方法
[ A | I ] ~ [ I | B ] ----> B即是A的逆阵
2.初等变换
(1) 对调矩阵中的任意两行(列)
(2) 以非零常数乘以矩阵中的某一行(列)中的所有元素
(3) 把矩阵中的某一行(列)的所有元素的k倍(k是常数)加到另一行(列)的对应元素上去
如果把矩阵A经过有限次初等变换变成矩阵B,就称矩阵A与B等价,记作A ~ B。
3.矩阵A可逆的充要条件:
A可表示为有限个初等矩阵的乘积
4. 行列式
行列式按行(列)展开法则
行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和。
性质及其推论:
(1) 行列式与它的转置行列式相等.
(2) 行列式中如果有两行(列)元素成比例,则此行列式等于零(包括有0行(列)、两行(列)相等).
(3) 若行列式的某一行(列)的元素都可分成两数之和,则行列式可分成两个对应行列式的和.
(4) 初等变换得到的行列式值的变化
将方阵A中的某行(列)乘以k得到B,则|B| = k|A|
将方阵A中的某行(列)的k倍加到另一行(列)得到B,则|B| = |A|
交换方阵A中的任两行(列)得到B,则|B| = -|A|
(5) 设A B 均为n阶方阵,则A与B的乘积矩阵的行列式等于A的行列式与B的行列式的乘积.即|AB| = |A| |B|
5.伴随阵和逆矩阵
(1)n阶矩阵A,则AA^* = A^*A = |A|I
(2)|A^*| = |A|^n
(3)A^-1 = A^*/|A|
其中
| A11 A21 ... An1 |
| A12 A22 ... An2 |
| . . . . |
| . . . . | = A^*
| . . . . |
| A1n A2n ... Ann |
6. 齐次线性方程组和非齐次线性方程组
(1) n元齐次线性方程组A m*n x = 0有非零解的充要条件是其系数矩阵的秩r(A) < n,且其通解中带有n-r(A)个任意参数。(m*n是矩阵的m行n列。非零解称为非平凡解,零解称为平凡解)
(2) n元非齐次线性方程组 Ax=b有解的充要条件是系数矩阵A的秩等于增广矩阵[A | b]的秩。
r(A) = r(A|b) = n 方程组有唯一解
r(A) = r(A|b) < n 方程组有无限多个解,且其通式中带有n-r(A)个任意参数
r(A) != r(A|b) 方程组无解
(暂用A|b来表示增广阵)
7. 向量空间
(1)给定向量组 a1, a2, ..,an,若存在不全为零的数k1, k2,...,kn,使得
k1a1 + k2a2 + ... + knan = 0,则称向量组是线性相关的。当且仅当k1 = k2 = .. = kn = 0时才成立,则称向量组是线性无关的。
(2)给定向量组 a1, a2, ..,an 线性相关的充要条件是由它所构成的矩阵A[a1, a2,..,an]的秩小于n。线性无关的充要条件是向量的秩等于n。
8.特征值问题与二次型
三角阵的特征值即为主对角线上的元素



以下是对线性代数中用到的性质和一些求解(持续跟新)。
package com.eric.matrix;
import java.util.Random;
/**
* @author Yuanbo Han
*/
/**
* @author Administrator
*
*/
public class Matrix {
private int line;
private int column;
private double[][] value;
private boolean containsZeroLineOrColumn;//为了使得计算行列式容易
private boolean isTriangularMatrix;//为了使得计算行列式容易
/* ----------------- 构造函数 -----------------*/
/**
* 产生一个有line行column列的一个矩阵,矩阵中的值没有被初始化。
* @param line
* @param column
*/
public Matrix(int line, int column) {
if(line <= 0 || column <= 0){
System.err.println("行列值必须是正数");
}else{
this.line = line;
this.column = column;
value = new double[line][column];
}
}
/**
* 产生一个有line行column列的一个矩阵,矩阵中的值在[min,max)
* @param line
* @param column
*/
public Matrix(int line, int column, int min, int max) {
super();
if(line <= 0 || column <= 0){
System.err.println("行列值必须是正数");
}else if(min > max){
System.err.println("最小值不能大于最大值");
}else{
this.line = line;
this.column = column;
value = new double[line][column];
for(int i=0;i<line;i++){
for(int j=0;j<column;j++){
value[i][j] = this.randomBetween(min,max);
}
}
this.initializeForDeterminant();
}
}
/**
* 讲一个二维数组指定到matrix
* @param value
*/
public Matrix(double[][] value) {
super();
if(value != null){
try {
this.value = value;
this.line = value.length;
this.column = value[0].length;
this.initializeForDeterminant();
} catch (Exception e) {
System.err.println("出入的矩阵格式不正确");
e.printStackTrace();
}
}else{
System.err.println("传入的矩阵不能为空");
}
}
public Matrix(Matrix matrix){
this.setMatrix(matrix);
}
/* ----------------- 计算函数 -----------------*/
public Matrix add(Matrix val){
if(this.isCalculableForAdd(val)){
Matrix matrix = new Matrix(this.getLine(),this.getColumn());
for(int i=0;i<this.getLine();i++){
for(int j=0;j<this.getColumn();j++){
matrix.getValue()[i][j] = this.value[i][j] + val.getValue()[i][j];
}
}
return matrix;
}
System.err.println("两个矩阵不能进行加法运算");
return null;
}
public Matrix subtract(Matrix val){
val = val.multiple(-1);
return this.add(val);
}
public Matrix multiple(Matrix val){
if(this.isCalculableForMultiple(val)){
Matrix matrix = new Matrix(this.getLine(),val.getColumn());
for(int i=0;i<this.getLine();i++){
for(int j=0;j<val.getColumn();j++){
double temp = 0;
for(int k=0;k<this.getColumn();k++){
temp += this.value[i][k] * val.getValue()[k][j];
}
matrix.getValue()[i][j] = temp;
}
}
return matrix;
}
System.err.println("两个矩阵不能进行乘法运算");
return null;
}
public Matrix pow(int exponent){
if(this.getLine() != this.getColumn()){
System.err.println("不能进行幂运算");
return null;
}else{
if(exponent >= 1){
Matrix matrix = Matrix.generateIdentityMatrix(this.getLine());
for(int i=0;i<exponent;i++){
matrix = matrix.multiple(this);
}
return matrix;
}else{
System.err.println("指数只能为正数");
return null;
}
}
}
/**
* 用m(系数)乘以矩阵
* @param m
* @return
*/
public Matrix multiple(double m){
for(int i=0;i<this.getLine();i++){
for(int j=0;j<this.getColumn();j++){
this.value[i][j] *= m;
}
}
return this;
}
/**
* 得到该矩阵的转置矩阵
* @return
*/
public Matrix transpose(){
Matrix matrix = new Matrix(this.getColumn(), this.getLine());
for(int i=0;i<this.getLine();i++){
for(int j=0;j<this.getColumn();j++){
matrix.getValue()[j][i] = this.value[i][j];
}
}
return matrix;
}
/**
* 计算行列式的时候,为了提高效率,进行了如下处理:
* 1 首先判断该行列式是否存在某行(列)为全零 行列式为0
* 2 是否存在某两行(列)成比例 行列式为0
* 3 是否是三角阵 行列式为对角线元素的乘积
* 4 然后再计算行列式,且行列式使用递归进行计算,递归结束的条件是行列式为三阶或者二阶
* 计算该矩阵的行列式
* @return
*/
public double det(){
if(this.getLine() != this.getColumn()){
System.err.println("只有方阵才能进行求行列式运算");
return 0;
}
if(this.isContainsZeroLineOrColumn()){
return 0;
} else if(this.isTriangularMatrix()){//三角阵的行列式是对角线元素的乘积
double result = 1;
for(int i=0;i<this.getLine();i++){
result *= this.value[i][i];
}
return result;
}else{
if(this.getLine() == 2 || this.getLine() == 3){//结束递归的条件
if(this.getLine() == 3){
double result =
this.value[0][0] * this.value[1][1] * this.value[2][2]
+ this.value[0][1] * this.value[1][2] * this.value[2][0]
+ this.value[0][2] * this.value[1][0] * this.value[2][1]
- this.value[0][2] * this.value[1][1] * this.value[2][0]
- this.value[0][0] * this.value[1][2] * this.value[2][1]
- this.value[0][1] * this.value[1][0] * this.value[2][2];
return result;
}else{
double result = this.value[0][0] * this.value[1][1] - this.value[1][0] * this.value[0][1];
return result;
}
} else{
double result = 0;
for(int j=0;j<this.getColumn();j++){
if(this.getValue()[0][j] != 0){
Matrix matrix = this.removeLineAndColumn(1, j+1);//总是以第一行来进行计算
result += this.getValue()[0][j] * Math.pow(-1, j) * matrix.det();//Math.pow(-1, j)应该是Math.pow(-1, 1+j+1) = Math.pow(-1, j);
}
}
return result;
}
}
}
/**
* 求该矩阵元素aij的代数余子式
* @param i
* @param j
* @return
*/
public double algebraicComplement_I_J(int i, int j){
if(this.getLine() != this.getColumn()){
System.err.println("只有方阵才能进行求代数余子式运算");
return 0;
}
if(i < 1 || j < 1 || i > this.getLine() || j > this.getColumn()){
System.err.println("传入的参数有错误");
return 0;
}
if(this.getLine() == 2 && this.getColumn() == 2){
return Math.pow(-1, i+j) * this.getValue()[i%2][j%2];
}else{
Matrix matrix = this.removeLineAndColumn(i, j);
return Math.pow(-1, i+j) * matrix.det();
}
}
/**
* 求该矩阵的伴随矩阵
* @return
*/
public Matrix adjA(){
if(this.getLine() != this.getColumn()){
System.err.println("只有方阵才能进行求伴随阵运算");
return null;
}
Matrix matrix = new Matrix(this.getLine(),this.getColumn());
for(int i=0;i<this.getLine();i++){
for(int j=0;j<this.getColumn();j++){
matrix.getValue()[i][j] = this.algebraicComplement_I_J(j+1, i+1);//将第j+1行,i+1列的代数余子式放到i+1行,j+1列.
}
}
return matrix;
}
/**
* 求该矩阵的逆矩阵
* @return
*/
public Matrix inverse(){
if(this.getLine() != this.getColumn()){
System.err.println("只有方阵才能进行求逆矩阵运算");
return null;
}
double det = this.det();
if(det != 0){
Matrix matrix = this.adjA();
System.out.println("--------原始的逆矩阵是----------");//考虑到有可能det不能被矩阵中的所有元素除以之后得到无限小数
System.out.print(matrix);
System.out.println(" * 1 / " + det);
System.out.println("-------------------------------");
matrix = matrix.multiple(1 / det);
return matrix;
}else{
System.err.println("行列式为0,故逆矩阵不存在");
return null;
}
}
/**
* 解方程组
* @param b
* @return
*/
public double[] solve(double[] b){
return null;
}
/**
* 得到矩阵的秩
* @return
*/
public int rank(){
return 0;
}
/**
* 得到矩阵的迹
* @return
*/
public double trace(){
return 0;
}
/**
* 产生一个line行 和 line列的单位矩阵
* @param line
* @return
*/
public static Matrix generateIdentityMatrix(int line){
if(line > 0){
Matrix matrix = new Matrix(line,line);
for(int i=0;i<line;i++){
matrix.getValue()[i][i] = 1;
}
return matrix;
}
return null;
}
@Override
public boolean equals(Object obj) {
if(obj == null || !(obj instanceof Matrix)){
return false;
}
Matrix matrix = (Matrix)obj;
if((matrix.getLine() != this.getLine()) || (matrix.getColumn() != this.getColumn())){
return false;
}else{
for(int i=0;i<this.getLine();i++){
for(int j=0;j<this.getColumn();j++){
if(this.value[i][j] != matrix.getValue()[i][j]){
return false;
}
}
}
}
return true;
}
@Override
public String toString() {
StringBuffer sb = new StringBuffer();
for(int i=0;i<value.length;i++){
sb.append("|\t");
for(int j=0;j<value[0].length;j++){
sb.append(value[i][j] + "\t");
}
sb.append("|\n");
}
sb.delete(sb.length()-1, sb.length());
return sb.toString();
}
/* ----------------- 辅助函数 -----------------*/
/**
* 传入的line参数是按照数学中的从1开始的
* @param line
* @param replacemant
* @return
*/
public Matrix replaceLine(int line, double[] replacemant){
if(line < 1 || line > this.getLine() || replacemant == null || replacemant.length != this.getColumn()){
System.err.println("不能用指定的内容替换原来中矩阵中的值");
return null;
}
Matrix matrix = new Matrix(this);
for(int j=0;j<this.getColumn();j++){
matrix.getValue()[line-1][j] = replacemant[j];
}
return matrix;
}
/**
* 传入的column参数是按照数学中的从1开始的
* @param column
* @param replacemant
* @return
*/
public Matrix replaceColumn(int column, double[] replacemant){
if(column < 1 || column > this.getColumn() || replacemant == null || replacemant.length != this.getLine()){
System.err.println("不能用指定的内容替换原来中矩阵中的值");
return null;
}
Matrix matrix = new Matrix(this);
for(int i=0;i<this.getLine();i++){
matrix.getValue()[i][column-1] = replacemant[i];
}
return matrix;
}
/**
* 传入的参数是按照数学中的从1开始的
* @param line
* @return
*/
public Matrix removeLine(int line){
if(line < 1 || line > this.getLine()){
System.err.println("传入的line值有问题");
return null;
}
Matrix matrix = new Matrix(this.getLine() - 1,this.getColumn());
int index = -1;
for(int i=0;i<this.getLine();i++){
if(i != (line - 1)){
index++;
for(int j=0;j<this.getColumn();j++){
matrix.getValue()[index][j] = this.getValue()[i][j];
}
}
}
return matrix;
}
/**
* 传入的column参数是按照数学中的从1开始的
* @param column
* @return
*/
public Matrix removeColumn(int column){
if(column < 1 || column > this.getColumn()){
System.err.println("传入的column值有问题");
return null;
}
Matrix matrix = new Matrix(this.getLine(),this.getColumn() - 1);
for(int i=0;i<this.getLine();i++){
int index = -1;
for(int j=0;j<this.getColumn();j++){
if(j != (column - 1)){
index++;
matrix.getValue()[i][index] = this.getValue()[i][j];
}
}
}
return matrix;
}
/**
* 传入的line,column参数是按照数学中的从1开始的
* @param line
* @param column
* @return
*/
public Matrix removeLineAndColumn(int line, int column){
if(line < 1 || column < 1 || line > this.getLine() || column > this.getColumn()){
System.err.println("传入的line或者column值有问题");
return null;
}
Matrix matrix = new Matrix(this.getLine() - 1,this.getColumn() - 1);
int _i = -1;
for(int i=0;i<this.getLine();i++){
if(i != (line - 1)){
_i++;
int _j = -1;
for(int j=0;j<this.getColumn();j++){
if(j != (column - 1)){
_j++;
matrix.getValue()[_i][_j] = this.getValue()[i][j];
}
}
}
}
return matrix;
}
/**
* 传入的line参数是按照数学中的从0开始的.
* 0的话代表将insertion插入到矩阵的第一行
* @param line
* @param insertion
* @return
*/
public Matrix addLineAfter(int line, double[] insertion){
if(line < 0 || line > this.getLine() || insertion == null || insertion.length != this.getColumn()){
System.err.println("不能将指定的内容插入到原来的矩阵中");
return null;
}
Matrix matrix = new Matrix(this.getLine() + 1, this.getColumn());
int distance = 0;
for(int i=0;i<this.getLine();i++){
for(int j=0;j<this.getColumn();j++){
if(i == line){//line 代表着将insertion插入到以数组0基础的line下标位置
for(int k=0;k<insertion.length;k++){
matrix.getValue()[i][j] = insertion[k];
}
distance = 1;
}
matrix.getValue()[i+distance][j] = this.getValue()[i][j];
}
}
if(line == this.getLine()){
for(int k=0;k<insertion.length;k++){
matrix.getValue()[line][k] = insertion[k];
}
}
return matrix;
}
/**
* 传入的column参数是按照数学中的从0开始的.
* 0的话代表将insertion插入到矩阵的第一列
* @param column
* @param insertion
* @return
*/
public Matrix addColumnAfter(int column, double[] insertion){
if(column < 0 || column > this.getColumn() || insertion == null || insertion.length != this.getLine()){
System.err.println("不能将指定的内容插入到原来的矩阵中");
return null;
}
Matrix matrix = new Matrix(this.getLine(), this.getColumn() + 1);
for(int i=0;i<this.getLine();i++){
int distance = 0;
for(int j=0;j<this.getColumn();j++){
if(j == column){//column 代表着将insertion插入到以数组0基础的column下标位置
matrix.getValue()[i][j] = insertion[j];
distance = 1;
}
matrix.getValue()[i][j+distance] = this.getValue()[i][j];
}
}
if(column == this.getColumn()){
for(int k=0;k<insertion.length;k++){
matrix.getValue()[k][column] = insertion[k];
}
}
return matrix;
}
/**
* 将after矩阵加入到矩阵的右面
* @param after
* @return
*/
public Matrix assembleHorizontal(Matrix after){
if(after == null){
return this;
}else if(after.getLine() != this.getLine()){
System.err.println("不能组合两个矩阵");
return null;
}else{
Matrix matrix = new Matrix(this.getLine(),this.getColumn() + after.getColumn());
for(int i=0;i<this.getLine();i++){
int index = 0;
for(int j=0;j<this.getColumn();j++){
matrix.getValue()[i][index] = this.getValue()[i][j];
index++;
}
for(int k=0;k<after.getColumn();k++){
matrix.getValue()[i][index] = after.getValue()[i][k];
index++;
}
}
return matrix;
}
}
/**
* 将after矩阵加到矩阵的下面
* @param after
* @return
*/
public Matrix assembleVertical(Matrix after){
if(after == null){
return this;
}else if(after.getColumn() != this.getColumn()){
System.err.println("不能组合两个矩阵");
return null;
}else{
Matrix matrix = new Matrix(this.getLine()+after.getLine(),this.getColumn());
for(int i=0;i<this.getLine();i++){
for(int j=0;j<this.getColumn();j++){
matrix.getValue()[i][j] = this.getValue()[i][j];
}
}
for(int i=0;i<after.getLine();i++){
for(int j=0;j<after.getColumn();j++){
matrix.getValue()[i+this.getLine()][j] = after.getValue()[i][j];
}
}
return matrix;
}
}
/* ----------------- 以下初等变换函数 -----------------*/
/**
* 交换第line1行和第line2行的内容
* 传入的line1和line2的值是数学中的从1开始的,而不是编程语言中的0
* @param line1
* @param line2
* @return
*/
public Matrix exchangeLine(int line1, int line2){
if(line1 < 1 || line2 < 1 || line2 > this.getLine() || line1 > this.getLine()){
System.err.println("传入的参数有误");
return null;
}
if(line1 == line2){
System.out.println("line1=line2,不需要交换");
return this;
}
Matrix matrix = new Matrix(this);
double[] temp = new double[matrix.getColumn()];
for(int j=0;j<matrix.getColumn();j++){
temp[j] = matrix.getValue()[line1-1][j];
}
for(int j=0;j<matrix.getColumn();j++){
matrix.getValue()[line1-1][j] = matrix.getValue()[line2-1][j];
}
for(int j=0;j<matrix.getColumn();j++){
matrix.getValue()[line2-1][j] = temp[j];
}
return matrix;
}
/**
* 交换第column1列与第column2列的内容
* 传入的column1和column2的值是数学中的从1开始的,而不是编程语言中的0
* @param column1
* @param column2
* @return
*/
public Matrix exchangeColumn(int column1, int column2){
if(column1 < 1 || column2 < 1 || column2 > this.getLine() || column1 > this.getLine()){
System.err.println("传入的参数有误");
return null;
}
if(column1 == column2){
System.out.println("column1=column2,不需要交换");
return this;
}
Matrix matrix = new Matrix(this);
double[] temp = new double[matrix.getLine()];
for(int i=0;i<matrix.getLine();i++){
temp[i] = matrix.getValue()[i][column1-1];
}
for(int i=0;i<matrix.getLine();i++){
matrix.getValue()[i][column1-1] = matrix.getValue()[i][column2-1];
}
for(int i=0;i<matrix.getLine();i++){
matrix.getValue()[i][column2-1] = temp[i];
}
return matrix;
}
/**
* 将第line行乘以k
* @param line
* @param k
* @return
*/
public Matrix r_i(int line, int k){
if(line < 1 || line > this.getLine()){
System.err.println("传入的参数有问题");
return null;
}
Matrix matrix = new Matrix(this);
for(int j=0;j<this.getColumn();j++){
matrix.getValue()[line-1][j] *= k;
}
return matrix;
}
/**
* 将第column列乘以k
* @param column
* @param k
* @return
*/
public Matrix c_i(int column, int k){
if(column < 1 || column > this.getColumn()){
System.err.println("传入的参数有问题");
return null;
}
Matrix matrix = new Matrix(this);
for(int i=0;i<this.getLine();i++){
matrix.getValue()[i][column-1] *= k;
}
return matrix;
}
/**
* 将第from行乘以k加到第to行
* from 和 to 都是从1开始的
* @param to
* @param from
* @param k
* @return
*/
public Matrix r_to_from_k(int to, int from, double k){
if(from < 1 || to < 1 || from > this.getLine() || to > this.getLine()){
System.err.println("输入的参数有误");
return null;
}
Matrix matrix = new Matrix(this);
for(int j=0;j<this.getColumn();j++){
matrix.getValue()[to-1][j] += (matrix.getValue()[from-1][j] * k);
}
return matrix;
}
/**
* 将第from列乘以k加到第to列
* from 和 to 都是从1开始的
* @param to
* @param from
* @param k
* @return
*/
public Matrix c_to_from_k(int to, int from, double k){
if(from < 1 || to < 1 || from > this.getColumn() || to > this.getColumn()){
System.err.println("输入的参数有误");
return null;
}
Matrix matrix = new Matrix(this);
for(int i=0;i<this.getLine();i++){
matrix.getValue()[i][to-1] += (matrix.getValue()[i][from-1] * k);
}
return matrix;
}
/* ----------------- 以上初等变换函数 -----------------*/
/**
* 为了使得行列式的计算可以提高效率而执行的一些操作,主要是初始化
* containsZeroLineOrColumn;
* isTriangularMatrix;
*/
private void initializeForDeterminant(){
this.containsZeroLineOrColumn();
this.triagularMatrix();
}
private void containsZeroLineOrColumn(){
for(int i=0;i<this.getLine();i++){
boolean contains = true;
for(int j=0;j<this.getColumn();j++){
if(this.getValue()[i][j] != 0){
contains = false;
break;
}
}
if(contains){
this.setContainsZeroLineOrColumn(true);
break;
}
}
if(!this.isContainsZeroLineOrColumn()){
for(int j=0;j<this.getColumn();j++){
boolean contains = true;
for(int i=0;i<this.getLine();i++){
if(this.getValue()[i][j] != 0){
contains = false;
break;
}
}
if(contains){
this.setContainsZeroLineOrColumn(true);
break;
}
}
}
}
private void triagularMatrix(){
boolean isTriagular = true;
for(int i=0;i<this.getLine()-1;i++){// 上三角矩阵
for(int j=i+1;j<this.getColumn();j++){
if(this.getValue()[i][j] != 0){
isTriagular = false;
break;
}
}
if(!isTriagular){
break;
}
}
if(isTriagular){
this.setTriangularMatrix(true);
}
if(!isTriagular){// 如果不是上三角阵
isTriagular = true;
for(int i=1;i<this.getLine();i++){// 下三角矩阵
for(int j=0;j<i;j++){
if(this.getValue()[i][j] != 0){
isTriagular = false;
break;
}
}
if(!isTriagular){
break;
}
}
if(isTriagular){
this.setTriangularMatrix(true);
}
}
}
/**
* 将指定的matrix中的value[][], line, column 指定到本类中
* @param matrix
*/
public void setMatrix(Matrix matrix){
this.setLine(matrix.getLine());
this.setColumn(matrix.getColumn());
this.value = new double[this.getLine()][this.getColumn()];
for(int i=0;i<this.getLine();i++){
for(int j=0;j<this.getColumn();j++){
this.value[i][j] = matrix.getValue()[i][j];
}
}
this.initializeForDeterminant();
}
/**
* 得到矩阵的深层拷贝
* @return
*/
public Matrix copy(){
Matrix matrix = new Matrix(this);
return matrix;
}
/**
* 得到指定位置的元素的值
* 是从1开始的
* @param i
* @param j
* @return
*/
public double get(int i, int j){
if(i < 1 || j < 1 || i > this.getLine() || j > this.getColumn()){
System.err.println("传入的参数有问题");
return Double.MIN_VALUE;
}
return this.getValue()[i-1][j-1];
}
/* ----------------- getter/setter 函数 -----------------*/
public int getLine() {
return line;
}
public void setLine(int line) {
this.line = line;
}
public int getColumn() {
return column;
}
public void setColumn(int column) {
this.column = column;
}
public double[][] getValue() {
return value;
}
public void setValue(double[][] value) {
this.value = value;
}
private double randomBetween(int min, int max){
int value = max - min;
return new Random().nextInt(value) + min;
}
private boolean isCalculableForAdd(Matrix val){
if(!val.isValidMatrix() || this.getLine() != val.getLine() || this.getColumn() != val.getColumn()){
return false;
}
return true;
}
private boolean isCalculableForMultiple(Matrix val){
if(!val.isValidMatrix() || this.getColumn() != val.getLine()){
return false;
}
return true;
}
private boolean isValidMatrix(){
if((this == null) || this.getLine() <= 0 || this.getColumn() <= 0){
return false;
}
return true;
}
public boolean isContainsZeroLineOrColumn() {
return containsZeroLineOrColumn;
}
public void setContainsZeroLineOrColumn(boolean containsZeroLineOrColumn) {
this.containsZeroLineOrColumn = containsZeroLineOrColumn;
}
public boolean isTriangularMatrix() {
return isTriangularMatrix;
}
public void setTriangularMatrix(boolean isTriangularMatrix) {
this.isTriangularMatrix = isTriangularMatrix;
}
public static void main(String[] args) {
Matrix matrix = new Matrix(new double[][]{{1,2,3},{2,2,1},{3,4,3}});
System.out.println("matrix");
System.out.println(matrix);
System.out.println("matrix.removeLine(1)");
System.out.println(matrix.removeLine(1));
System.out.println("matrix.removeColumn(1)");
System.out.println(matrix.removeColumn(1));
System.out.println("matrix.removeLineAndColumn(1, 1)");
System.out.println(matrix.removeLineAndColumn(1, 1));;
System.out.println("matrix.replaceLine(1, new double[] { 4, 4, 4 })");
System.out.println(matrix.replaceLine(1, new double[] { 4, 4, 4 }));
System.out.println("matrix.replaceColumn(1, new double[] { 4, 4, 4 })");
System.out.println(matrix.replaceColumn(1, new double[] { 4, 4, 4 }));
System.out.println("matrix.addLineAfter(2, new double[] { 4, 4, 4 })");
System.out.println(matrix.addLineAfter(2, new double[] { 4, 4, 4 }));
System.out.println("matrix.addColumnAfter(3, new double[] { 4, 4, 4 })");
System.out.println(matrix.addColumnAfter(3, new double[] { 4, 4, 4 }));
System.out.println("matrix.exchangeLine(1, 2)");
System.out.println(matrix.exchangeLine(1, 2));
System.out.println("matrix.exchangeColumn(1, 2)");
System.out.println(matrix.exchangeColumn(1, 2));
System.out.println("matrix.c_i(1, 2)");
System.out.println(matrix.c_i(1, 2));
System.out.println("matrix.r_i(1, 2)");
System.out.println(matrix.r_i(1, 2));
System.out.println("matrix.c_to_from_k(1, 2, 1)");
System.out.println(matrix.c_to_from_k(1, 2, 1));
System.out.println("matrix.r_to_from_k(1, 2, 1)");
System.out.println(matrix.r_to_from_k(1, 2, 1));
System.out.println("matrix.algebraicComplement_I_J(3, 1)");
System.out.println(matrix.algebraicComplement_I_J(3, 1));
System.out.println("matrix.det()");
System.out.println(matrix.det());
System.out.println("matrix.adjA()");
System.out.println(matrix.adjA());
System.out.println("matrix.inverse()");
System.out.println(matrix.inverse());
Matrix matrix2 = new Matrix(new double[][]{{2,3,4},{5,6,7},{8,9,10}});
System.out.println("matrix2");
System.out.println(matrix2);
System.out.println("matrix.assembleHorizontal(matrix2)");
System.out.println(matrix.assembleHorizontal(matrix2));
System.out.println("matrix.assembleVertical(matrix2)");
System.out.println(matrix.assembleVertical(matrix2));
Matrix matrix3 = new Matrix(new double[][]{{3,0,0,0},{3,2,4,1},{-1,0,5,0},{2,0,6,-1}});
System.out.println("matrix3");
System.out.println(matrix3);
System.out.println("matrix3.det()");
System.out.println(matrix3.det());
System.out.println(new Matrix(new double[][] {{0,0,0},{1,2,3}, {2,3,4}}).det());//存在0行的矩阵
System.out.println(new Matrix(new double[][] {{1,2,0},{2,3,0}, {3,4,0}}).det());//存在0列的矩阵
System.out.println(new Matrix(new double[][] {{1,0,0},{1,2,0},{1,2,3}}).det());//上三角矩阵
System.out.println(new Matrix(new double[][] {{1,2,3},{0,1,2},{0,0,1}}).det());//下三角矩阵
}
}