图论算法-求（有向）图中任意两点间所有路径

 

求（有向）图中任意两点间所有路径

1建图：

     图类中包括如下信息：顶点集合，邻接矩阵。

     节点类中包括如下信息：是否被访问过，节点的名称，从这个节点访问到下一个节点的集合

 

 <!--[endif]-->

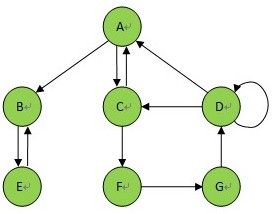
图1

 <!--[endif]-->

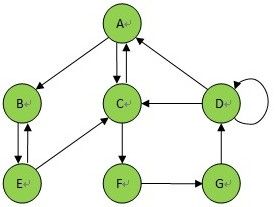
图2

 

2 算法思路

  A 将始点设置为已访问，将其入栈

  B 查看栈顶节点V在图中，有没有可以到达、且没有入栈、且没有从这个节点V出发访问过的节点

  C 如果有，则将找到的这个节点入栈

  D 如果没有，则将节点V访问到下一个节点的集合中每个元素赋值为零，V出栈

  E 当栈顶元素为终点时，设置终点没有被访问过，打印栈中元素，弹出栈顶节点

  F 重复执行B – E,直到栈中元素为空

 

 

package util;

public class Graph {

	private Vertex vertexList[]; // list of vertices
	private int adjMat[][]; // adjacency matrix

	private int nVerts;
	private static int MAX_VERTS = 7; // n个点

	int i = 0;
	int j = 0;

	public Vertex[] getVertexList() {
		return vertexList;
	}

	public int[][] getAdjMat() {
		return adjMat;
	}

	public int getN() {
		return MAX_VERTS;
	}

	public Graph(int index) {
		adjMat = new int[MAX_VERTS][MAX_VERTS]; // 邻接矩阵
		vertexList = new Vertex[MAX_VERTS]; // 顶点数组
		nVerts = 0;

		for (i = 0; i < MAX_VERTS; i++) {
			for (j = 0; j < MAX_VERTS; j++) {
				adjMat[i][j] = 0;
			}
		}

		addVertex('A');
		addVertex('B');
		addVertex('C');
		addVertex('D');
		addVertex('E');
		addVertex('F');
		addVertex('G');

		addEdge(0, 1);
		addEdge(0, 2);
		addEdge(1, 4);
		addEdge(2, 0);
		addEdge(2, 5);
		addEdge(3, 0);
		addEdge(3, 2);
		addEdge(3, 3);
		addEdge(4, 1);
		addEdge(4, 2);
		addEdge(5, 6);
		addEdge(6, 3);

		switch (index) {
		case 0:
			break;
		case 1:
			delEdge(4, 2);
			break;
		default:
			break;
		}
	}

	private void delEdge(int start, int end) {
		adjMat[start][end] = 0;
	}

	private void addEdge(int start, int end) {// 有向图，添加边
		adjMat[start][end] = 1;
		// adjMat[end][start] = 1;
	}

	public void addVertex(char lab) {
		vertexList[nVerts++] = new Vertex(lab);// 添加点
	}

	public char displayVertex(int i) {
		return vertexList[i].getLabel();
	}

	public boolean displayVertexVisited(int i) {
		return vertexList[i].WasVisited();
	}

	public void printGraph() {
		for (i = 0; i < MAX_VERTS; i++) {
			System.out.print("第" + displayVertex(i) + "个节点:" + " ");

			for (j = 0; j < MAX_VERTS; j++) {
				System.out.print(displayVertex(i) + "-" + displayVertex(j)
						+ "：" + adjMat[i][j] + " ");
			}
			System.out.println();
		}

	}

}

 package util;

import java.util.ArrayList;

public class Vertex {

	boolean wasVisited; // 是否遍历过
	public char label; // 节点名称
	ArrayList<Integer> allVisitedList;// 节点已访问过的顶点

	public void setAllVisitedList(ArrayList<Integer> allVisitedList) {
		this.allVisitedList = allVisitedList;
	}

	public ArrayList<Integer> getAllVisitedList() {
		return allVisitedList;
	}

	public boolean WasVisited() {
		return wasVisited;
	}

	public void setWasVisited(boolean wasVisited) {
		this.wasVisited = wasVisited;
	}

	public char getLabel() {
		return label;
	}

	public void setLabel(char label) {
		this.label = label;
	}

	public Vertex(char lab) // constructor
	{
		label = lab;
		wasVisited = false;
	}

	public void setVisited(int j) {
		allVisitedList.set(j, 1);

	}

}

 package util;

import java.util.ArrayList;
import java.util.Stack;

public class AF {

	boolean isAF = true;
	Graph graph;
	int n;
	int start, end;
	Stack<Integer> theStack;

	private ArrayList<Integer> tempList;
	private String counterexample;

	public AF(Graph graph, int start, int end) {
		this.graph = graph;
		this.start = start;
		this.end = end;
	}

	public boolean getResult() {
		graph.printGraph();
		n = graph.getN();
		theStack = new Stack<Integer>();

		if (!isConnectable(start, end)) {
			isAF = false;
			counterexample = "节点之间没有通路";
		} else {
			for (int j = 0; j < n; j++) {
				tempList = new ArrayList<Integer>();
				for (int i = 0; i < n; i++) {
					tempList.add(0);
				}
				graph.getVertexList()[j].setAllVisitedList(tempList);
			}

			isAF = af(start, end);
		}
		return isAF;
	}

	private boolean af(int start, int end) {
		graph.getVertexList()[start].setWasVisited(true); // mark it
		theStack.push(start); // push it

		while (!theStack.isEmpty()) {
			int v = getAdjUnvisitedVertex(theStack.peek());
			if (v == -1) // if no such vertex,
			{
				tempList = new ArrayList<Integer>();
				for (int j = 0; j < n; j++) {
					tempList.add(0);
				}
				graph.getVertexList()[theStack.peek()]
						.setAllVisitedList(tempList);// 把栈顶节点访问过的节点链表清空
				theStack.pop();
			} else // if it exists,
			{
				theStack.push(v); // push it
			}

			if (!theStack.isEmpty() && end == theStack.peek()) {
				graph.getVertexList()[end].setWasVisited(false); // mark it
				printTheStack(theStack);
				System.out.println();
				theStack.pop();
			}
		}

		return isAF;
	}

	// 判断连个节点是否能连通
	private boolean isConnectable(int start, int end) {
		ArrayList<Integer> queue = new ArrayList<Integer>();
		ArrayList<Integer> visited = new ArrayList<Integer>();
		queue.add(start);
		while (!queue.isEmpty()) {
			for (int j = 0; j < n; j++) {
				if (graph.getAdjMat()[start][j] == 1 && !visited.contains(j)) {
					queue.add(j);
				}
			}
			if (queue.contains(end)) {
				return true;
			} else {
				visited.add(queue.get(0));
				queue.remove(0);
				if (!queue.isEmpty()) {
					start = queue.get(0);
				}
			}
		}
		return false;
	}

	public String counterexample() {
		for (Integer integer : theStack) {
			counterexample += graph.displayVertex(integer);
			if (integer != theStack.peek()) {
				counterexample += "-->";
			}
		}

		return counterexample;
	}

	// 与节点v相邻，并且这个节点没有被访问到，并且这个节点不在栈中
	public int getAdjUnvisitedVertex(int v) {
		ArrayList<Integer> arrayList = graph.getVertexList()[v]
				.getAllVisitedList();
		for (int j = 0; j < n; j++) {
			if (graph.getAdjMat()[v][j] == 1 && arrayList.get(j) == 0
					&& !theStack.contains(j)) {
				graph.getVertexList()[v].setVisited(j);
				return j;
			}
		}
		return -1;
	} // end getAdjUnvisitedVertex()

	public void printTheStack(Stack<Integer> theStack2) {
		for (Integer integer : theStack2) {
			System.out.print(graph.displayVertex(integer));
			if (integer != theStack2.peek()) {
				System.out.print("-->");
			}
		}
	}

}

 import util.AF;

import util.Graph;

public class Main {

	public static void main(String[] args) {
        //第几张图，有两张(0,1)，起点序号(0-6)，终点序号(0-6)
		AF operation = new AF(new Graph(0), 3, 6);
		operation.getResult();

	}
}