内部排序(待续……)
- 插入排序 直接插入排序 折半插入排序 二路插入排序 表插入排序 希尔排序
- 交换排序 冒泡排序 快速排序
- 选择排序 简单选择排序 堆排序
- 归并排序 2-路归并排序
- 基数排序
1 插入排序
1.1直接插入排序
从第2个元素起,将第i个元素插入前i-1个有序的元素中。从i-1位置向前遍历寻找插入位置,边寻找插入位置边后移元素。
/**
* 直接插入排序:
* 将第i个元素插入前有序的i-1个序列中
*/
public static void insertSort(int src[]){
int len=src.length,j=0;
int guard=0;
for(int i=1;i<len;i++){//准备插入第i个元素
guard=src[i];
for(j=i-1;j>=0 && src[j]>guard;j--){//如果src[0]位置空出来的话,就将它设置为哨兵,能较少比较的次数
//这里每次不需要每次都交换元素
src[j+1]=src[j];//后移
}
src[j+1]=guard;//到位需要插入的元素
}
}
1.2折半插入排序
在直接插入排序的基础上用二分查找寻找插入位置,减少比较次数,移动元素的次数相同。
/**
* 折半插入排序
* 再直接插入排序的基础上通过折半查找算法
* 减少了定位src[i]插入点的时候比较的次数,
* 但是元素后移的次数不变
* @param src
*/
public static void bInsetSort(int src[]){
int len=src.length,j=0;
int low=0,high=0,mid=0;//折半查找的指针
int guard=0;//保存src[i]
for(int i=1;i<len;i++){
guard=src[i];
low=0;high=i-1;
//1 在src[low…high]中折半查找有序插入的位置
while(low<=high){
mid=(low+high)/2;
if(src[mid]>=guard){//插入点在低半区
high=mid-1;
}else{//插入点在高半区
low=mid+1;
}
}
//while最后一次循环有两种情况(guard一直都在low~high范围内):
//1 low==high,若src[mid]>=guard,保证稳定的插入点在high+2位置,high+1位置亦可插入
//若src[mid]<guard,保证稳定的插入点在high+1位置,high+2不可插入
//2 high=low+1,的情况都会转化为low==high的情况,而high=low+j(j>=2)的情况都回也都回转化
//2 记录后移
for(j=i-1;j>=high+1;j--){//不一定稳定后移
src[j+1]=src[j];
}
src[high+1]=guard;
}
}
1.3二路插入排序
用到一个新的数组。 int src[] = {49,38,65,97,76,13,27, 49}
第一步
| final | first | |||||||
| 49 | * | * | * | * | * | * | * | 38 |
第二步
| final | first | ||||||
| 49 | 65 | * | * | * | * | * | 38 |
第三步
| final | first | ||||||
| 49 | 65 | 97 | * | * | * | * | 38 |
第四步
| final | first | ||||||
| 49 | 65 | 76 | 97 | * | * | * | 38 |
第五步
| final | first | ||||||
| 49 | 65 | 76 | 97 | * | * | 13 | 38 |
第六步
| final | first | ||||||
| 49 | 65 | 76 | 97 | * | 13 | 27 | 38 |
第七步
| final | first | ||||||
| 49 | 49 | 65 | 76 | 97 | 13 | 27 | 38 |
1.4表插入排序
用静态链表的存储结构。
1.5希尔排序

/**
* 希尔排序
* 按增量序列dlta[0…t-1]分别使相隔某个增量的
* 子序列有序,直到最后的增量为1,整个序列都
* 有序
* @param src
*/
public static void shellSort(int src[],int dlta[]){
int t=dlta.length;
//按增量dlta[0…t-1]堆顺序表src做希尔排序
for(int k=0;k<t;k++){
shellInsert(src,dlta[k]);
}
}
private static void shellInsert(int src[],int dk){
int len=src.length;
int third,j;
//对序列src做一趟插入排序,相比于直接插入排序,增量变为dk
for(int i=dk;i<len;i++){//将元素src[i]插入合适的位置
third=src[i];
for(j=i-dk;j>=0 && src[j]>third;j-=dk){
src[j+dk]=src[j]; //记录后移
}
src[j+dk]=third; //插入合适的位置
}
}
2交换排序
2.1冒泡排序
/**
* 冒泡排序
* 从前往后比较的同时交换元素,最终将最大的元素置于最后的位置
*
* 改进的空间是:在一趟排序过程中没有交换记录的操作就结束整个排序过程
*/
public static void bubbleSort(int src[]){
int len=src.length;
int third=0;
boolean flag=false;
for(int i=len-1;i>0;i--){//选出src[i]位置的元素
flag=false;
for(int j=0;j<i;j++){
if(src[j]>src[j+1]){
//交换元素
third=src[j+1];
src[j+1]=src[j];
src[j]=third;
flag=true;
}
}
if(!flag){
break;
}
}
}
2.2快速排序
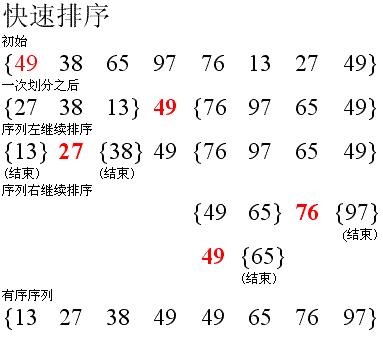
快速排序使用分治思想,用枢轴元素将整个序列分为两块,分块的时候从两头向中间遍历一次。
快速排序一次交换:

快速排序整个过程:
/**
* 快速排序
* 确定枢轴元素,然后将小的置于中轴元素之前,大的置于中轴元素之后
* 递归这个过程直到结束
* @param src
*/
public static void qSort(int src[],int low,int high){
if(low<high){//只剩下一个元素的时候就结束递归
int pivotLoc=partition(src,low,high);
qSort(src,low,pivotLoc-1);//对低子表进行排序,其中pivotLoc是枢轴位置
qSort(src,pivotLoc+1,high);//对高子表进行排序
}
}
//快速排序中一趟排序的算法
//交换子表中src[low…high]的记录,枢轴元素到位,并返回其位置,此时
//在它之前(后)的元素均不大(小)于它
private static int partition(int src[],int low,int high){
int pivot=src[low];//用子表的第一个记录做枢轴元素
while(low<high){
//从两天遍历向中间靠拢,只遍历一次,不回溯
while(src[high]>=pivot && low<high){high--;}
src[low]=src[high];//把比枢轴元素小的元素移动到低端
while(src[low]<=pivot && low<high){low++;}
src[high]=src[low];
}
//只有当low==high才结束循环,此时src[low]之前的元素都能保证小于枢轴元素,
//之后的元素都能保证大于枢轴元素。并且已经保存了该位置的副本,故low(或high)
//位置就是枢轴元素要插入的位置
src[low]=pivot;
return low;
}
3选择排序
3.1简单选择排序
选出最小的元素与i位置的元素交换,选择的过程中无需交换只需保存最小元素的索引值。
/**
* 简单选择排序
* 通过n-i趟比较选出最小的元素与i位置的元素交换(选择过程中无需移动元素)
*/
public static void selectSort(int src[]){
int min=0,len=src.length;
int third=0;
for(int i=0;i<len;i++){
min=i;
for(int j=i+1;j<len;j++){
if(src[j]<src[min]){min=j;}
}
//将一趟比较后最小的元素移动到src[i]
third=src[min];
src[min]=src[i];
src[i]=third;
}
}
3.2堆排序
堆定义:
小顶堆:k(i)<=k(2i) && k(i)<=k(2i+1)
大顶堆:k(i)>=k(2i) && k(i)>=k(2i+1)
(i=1,2,…,n/2向下取整)
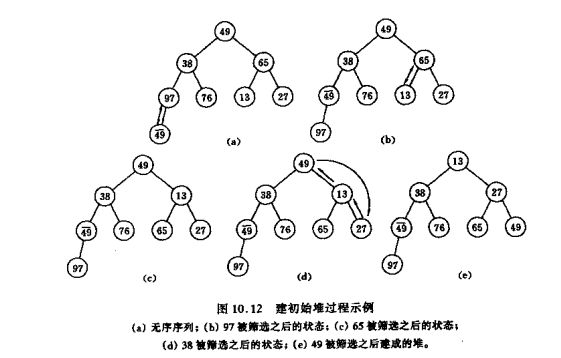
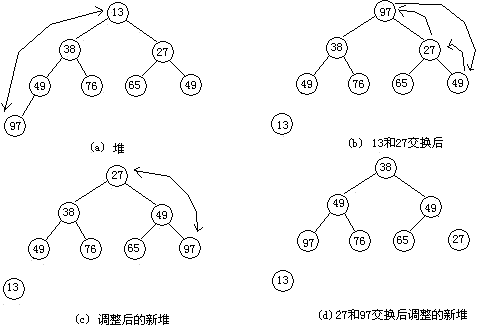
1 先将无序序列调整堆结构
2 将堆顶元素和最后一个位置i的元素交换并调整0…i-1元素为新堆。
3 继续第2步直到堆顶元素就是最后一个元素的时候结束。
/**
* 堆排序
* @param src
*/
public static void headSort(int src[]){
int third=0;
//因为叶子节点均满足堆条件,所以从src.length/2位置开始
for(int i=src.length/2-1;i>=0;i--){//把src[1…src.length]建成大顶堆
heapAdjust(src,i,src.length-1);
}
for(int i=src.length-1;i>0;i--){//将堆顶记录和src[i]交换,并将src[0…i-1]重新调整为堆结构
third=src[0];
src[0]=src[i];
src[i]=third;
heapAdjust(src,0,i-1);
}
}
//在除了s位置均满足堆条件的序列src[s…m]上将s插入合适的位置形成堆
private static void heapAdjust(int src[],int s,int m){
//src[s…m]除src[s]之外均满足堆的定义
//本函数调整src[s]的位置,使src[s…m]
//变成一个大顶堆
int rc=src[s];
for(int j=2*s+1;j<=m;j=j*2+1){
if(j<m && src[j]<src[j+1]){
//j<m保证有右子节点
j++; //j为较大记录的下标
}
if(rc>=src[j]){break;}//third应该在位置s上
src[s]=src[j];s=j;
}
src[s]=rc; //插入
}
归并排序
2-路归并排序

/**
* 2-路归并排序的递归表示:
* 思想是平分序列从小到大归并
* 而递归的时候表示为自顶向下递归直到s==t
*/
public static void mergerSort(int src[]){2-12
mSort(src,0,src.length-1);
}
private static void mSort(int src[],int s,int t){
int m;
//将src[s…t]归并排序为有序的
if(s<t){
m=(s+t)/2; //平分
mSort(src,s,m); //递归的归并前半部分
mSort(src,m+1,t);
merge(src,s,m,t);
}
}
private static void merge(int src[],int i,int m,int n){
//将有序的src[i…m]和src[m+1…n]归并为有序的tr[i…n]
int tr[]=new int[n+1];
int k=i,j=m+1,low=i;
while(i<=m && j<=n){//将src记录由小到大归并入tr
if(src[i] <= src[j]){tr[k++]=src[i++];}
else tr[k++]=src[j++];
}
//将剩余的放入数组
while(j<=n) tr[k++]=src[j++];
while(i<=m) tr[k++]=src[i++];
//将结果拷贝回
for(k=low;k <= n;k++){src[k]=tr[k];}
}
基数排序