参考博客: http://blog.csdn.net/doc_sgl/article/details/11805519
Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example,
Given height = [2,1,5,6,2,3],
return 10.
我觉得可以这么想,如果给你一个递增的数组,你怎么计算!
栈用来存索引!height中的下标 , 而且必须是递增的索引!(索引对应的值是必须的)
如果等待进栈的元素的值小于栈顶元素,那么就对栈中大于该值的元素出栈,并计算面积!
这一步,不就是在这一个升序的数组里面,高度大于等待进栈的元素的面积不就已经确定了吗?
比如说,1 , 5 , 6 , 2 ,当元素2的下标等待进栈时,那么高度为 5 或 6 的宽度不就确定了吗 , 一个
为 2 , 一个 为1 ,但是对于高度为1 ,你的宽度可不单单就是3 , 你还可以与2相连 ,宽度为4 ,然后2 后面的元素!
总之,你都要把高度为height[i]的面积算出来,
无论你是O(n^2) 的算法,还是 0(n)的算法
只不过O(n)的算法,它不是想O(n^2)的算法那样,以height[i]开头,然后 i+1 ,i+2....
通过栈,实现了在一个升序的数组里面计算!一次遍历即可!
public class Solution {
public int largestRectangleArea(int[] height) {
int len = height.length;
if(len <= 0 ) return 0;
LinkedList<Integer> stack = new LinkedList<>();
int[] extHt = Arrays.copyOf(height ,len + 1);
int maxArea = 0;
for(int i = 0 ; i < len + 1 ;) {
if(stack.isEmpty() || extHt[stack.getLast()] < extHt[i])
stack.add(i++);
else {
// 栈顶元素>height[i] 出栈
int top = stack.removeLast();
int width = 0;
// 注意 如果top 是里面的最后一个元素,那么只有两种可能,一它是最小的元素,而它是第一个元素
// 最小的元素对应的 i 就是 len 第一个元素 对应的i = 1
if(stack.isEmpty()) width = i;
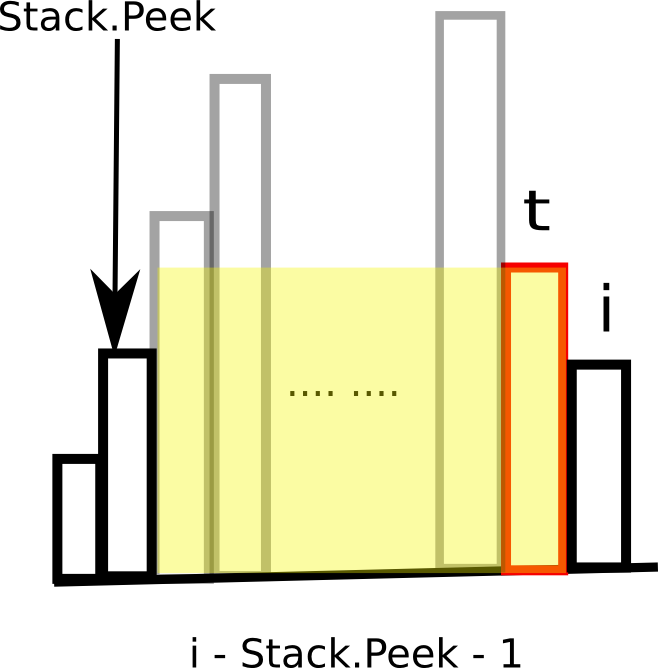
// 这个求width的长度可以参照下图
else width = i - stack.getLast() - 1;
//这句话的意思,可以理解成 第top 个元素 在他所属的升序子集中的面积!
maxArea = Math.max(maxArea , extHt[top] * width);
}
}
return maxArea;
}
}
我想我知道这中算法为什么是对的了?
如果给你一个递增的数组 : 1 3 5 6 9 12 你会就算!
12 , 9 和 12 = 18 , 6 9 和 12 = 18 ,5 6 9 和 12 = 20 ,3 5 6 9 12 = 20 ......
同样对于 ,一个乱序的数组,乱序中也有顺序 ,比如 2 ,1 ,5 ,6 , 2 ,3
按照上面算法的思路 : 2 1 降序了,可以看成1左边是一个升序的子集,而不是一个元素,那么就按照从后向前
计算最大面积!直到满足1加进来后,又是一个升序的 , 然后又可以这样了吗。
1 , 5 , 6 ,到2的时候,不满足升序了 ! 从后往前 直到 1 .
那么,这里有一个问题,你为什么不连1也一块计算了!
因为1 你 能够和后面的元素 又构成一个新的升序数组,也就是说,与1公共的面积不单单只有这一块!2 , 3 与 1都有公共的面积!
可以想象一个数组的最小元素,那么它的公共面积 是不是 size * min !