为什么交通信号灯需要红绿两色?
我们在十字路口,看到红灯停、绿灯行,这时有没有想过,为什么交通信号灯需要两种颜色(黄灯其实只是让人提前有所准备的红灯而已)?这里面其实包含了有趣的数学原理。
仔细想想,交通灯的目的在于什么呢?就是通过引导人们的行动方式防止危险发生,提高安全保障。因此,协调好路口上不同方向间红绿灯的色彩,就成了交通灯设计时要考虑的核心因素。
下面举个具体的例子来说明这个问题,首先我们要建立一些概念;假设有路口如下所示:

这是一个典型的十字路口,我们可以将四条路用方向来命名,上面的叫北路(N),左边的为西路(W);S,E同理。于是上右下左四条路分别为N、E、S、W。
接下来要描述行进方式:如果我们要从北向南行进,我们将之称为N -> S;如果从南路右转弯到东路,则为S -> E;那么从北路过来,左转弯到东路则是N -> E,非常简单。
因此,我们可以知道,对于每一个方向过来的人们,TA们看到的交通灯的颜色,将决定TA们的行动。比如假设有从北向南(即N->S)的人们此时在通行,那么就不能允许由东向西(即E->W)的人通过。因此,在交通灯设计时,我们称N->S与E->W为 “互斥“ 的:
对于互斥的行进方向,交通灯必须显示不同的颜色
因此,根据这个原理,如果N->S通行时,假设用颜色A来表示可通过的状态,这一方向上的人们看到的交通灯颜色则为A;此时E->W方向上的交通灯颜色就应该为颜色B,B表示此时不可通行,总之两个方向上面的交通灯颜色不能一样,否则同时通行的话后果严重。这个很容易理解:北向南行进的人看到的是绿灯的话,东西向的人们肯定看到的红灯。
那么对于由北向南和由南向北的车辆如何呢?N->S和S->N应该是同时被允许的,北向南与南向北通行的人们互不干扰,因为两个方向的人都靠各自的右方通行的话,是不会撞在一起的。因此这两个方向上的人们应该在同一时间段内看到的是同一种颜色的交通灯:它们要么同时可以通行,要么同时需要停下来。
因此设计交通灯时,我们需要考虑的是找出一个路口上面所有的"互斥"状态。比如N->S与E->W是互斥的,它们必须用两种不同的颜色来表示(北向南是绿灯时,东向西必须为红灯)。那么:
到底用多少种颜色,可以将所有的互斥状态标记完全呢?(两种颜色就够吗?)
上面这个问题就是交通灯设计的本质问题。为了解决这个问题,我们首先列出所有可能的行进方向:
将上面的写法简化一下,便得到了:
如果把上面的几个行进方向变成点,我们就可以得到下面这张图:
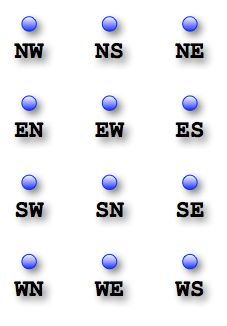
从上图中可以看到:
有了这些点以后,将那些互斥的行进方向(也就是上图中的各点)之间连线,所有这些互斥的状态之间便有了线连接。
刚才已经说过,南北通行方为绿灯时,东西方向应该是红灯,那么也就是说:NS,SN,与EW,WE之间是互斥的,于是我们便将NS <--> EW,NS <--> WE,SN <--> EW,SN <--> WE之间连线获得下图:
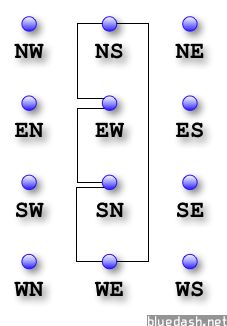
因为被连线的两个端点看到的信号灯的颜色不能一致,根据这条原则,我们将上图涂色:
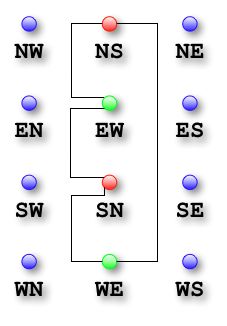
仔细看上面这张图:
因此,交通灯设计的问题就转化成涂色问题:首先根据事实需要,总结出哪些行进方向之间有冲突,将其转化为点与点之间的连接;然后,这些有冲突的方向的信号灯颜色要设计成不一样,实际上就是为图中所有线两端的点涂上不同的颜色。
上面这个问题是数学里面的一个研究领域,叫做图论。而“用最少的颜色填图”这个细分领域又有它自己的名字,叫做 “NP-complete problems”。这个研究方向一直是数学领域研究的难点,直到现在,人类也并没有找到特别有效的解决办法:基本上现有的方法都可以理解成“把所有的可能都试一遍,两个颜色不成试三个,三个不成试四个。。。”;
用不同的颜色去涂其实并不难,因为我们完全可以用各种各样的颜色,多得用不完。但难就难在如何去证明所用的颜色是最少的。目前数学界还没能完全攻克这个难题,留给后人继续努力。
但这并不是说我们对这类问题束手无策,数学的魅力在于,在研究一个问题的过程中,会产生很多对人类有帮助的工具,而这些工具,本身比证明一个结果更重要。此外,我们在研究这个问题的时间,可能不能完全解决它,但可以部分的解决掉。拿本文的涂色问题来讲,我们现在虽然不能完全的解决掉它,但我们可以对满足一些特殊要求的图有很好的解决方案和工具,在文章的最后部分我会举出一个例子。先回到文本讨论的内容上:
对于十字路口交通信号灯这种比较简单的问题,我们一个一个的用手去填色也花不了多久,只需要把有冲突的点连好线,然后试着用最少的颜色去涂就成了。此外,因为我们已经预先知道答案,红绿两色肯定是够用的,因此解答这个问题本身毫无难度。下面是实际操作的过程:
不断重复上面的过程,直到所有的点都被涂色,我们就得到了涂好颜色的图。但是有很重要的一点:
这样涂出来的图,用到的颜色不一定是最少的。
还记得我刚才介绍过的吗:去证明用了最少的颜色,是数学难题,你可以花一辈子在研究这个上面。
但是对于本文所讲的这个极其简单的问题,证明起来还是很容易的:因为一条线至少有两个端点,两个端点颜色不能一样,那么至少要用到两种颜色。因此,只要我们只用了两种颜色,那肯定就是最少颜色的情况了。
下面是一个完整的最终涂好颜色的图:
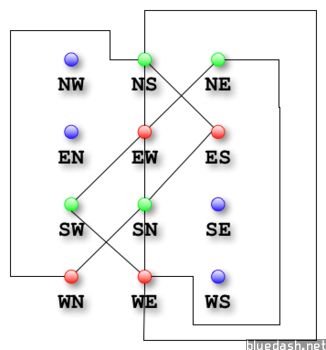
涂色的结果是两种颜色够用了。
接下来我们想想,有没有我们在日常生活中见到的路口,两种颜色的交通灯不够用?其实在大城市的道路上,这种情况还是挺普遍的,比如下面这种左转弯交通灯:
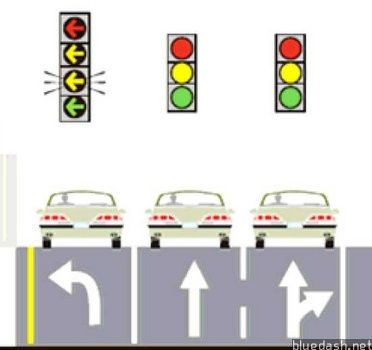
左转弯的时候,要看专门的左转弯灯,直行绿灯放行时,是不可以左转弯的。在这个设计当中,虽然左转弯灯仍然是用绿色表通行,实际上它是红、绿之外的第“三”种颜色。因为单纯靠绿色已经无法区分是直行放行还是左转弯放行了,这个交通灯用“绿色”+“左转弯箭头”的方式,实现了“第三种颜色”。之所以要这样设计,是因为用绿色的附合大众约定俗成的“红灯停,绿灯行”的思维定势,实际上,用别的颜色也可以的,但大部分人可能看不懂信号灯的含义了。
我们要关心的问题是:为什么这种情况下需要第三种颜色呢?还是让我们回到填色图中去找答案,所谓左转弯指示指,实际上等于添加了下面这条限制条件,即:
同方向和垂直方向直行时,不允许左转弯
没有左转弯指示灯的路口,只要直行方向绿灯就可以左转弯的,和垂直方向不冲突;而加上左转弯指示灯,等就是在图中这几个端点之间加了线:
看起来似乎很复杂,但其实这时我们不需要把上面的线全部画出来,就可以判断出此时至少需要三种颜色才够用。为什么?我们可以把以下几条线挑出来:
在加了左转弯的限制条件后,至少图中有上面三条线,把它画在图里:
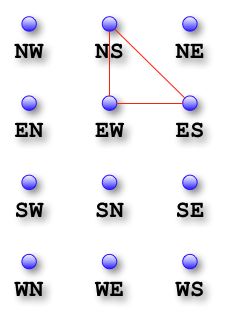
会发现,都不必考虑别的线,仅仅是这三个点之间的线,它们两两连通,而我们要想让它们之间的线段两端颜色不同,则至少需要三种颜色:

这就是左转向灯背后的数学原理。从上图中我们可以看中,这三个点之间,两两连通,至少需要3种不同的颜色才可能按要求涂色。这种完全连通的图,在图论里面有一个专门的名词去称呼,叫做"k-clique"。对于"k-clique"图的定义如下:
假设一张图里面有k个点,它们两两之间全部有线连通,我们称之为"k-clique"图。
对于k-clique图,有下述规律:
如果要求"k-clique"图中,线段两端的端点涂不同颜色,则至少需要k种颜色。
因此,对于上面3个点,互相完全连通的图就是一个"3-clique"图,至少需要三种颜色。我们可以看到,虽然图论还未能完全解决“最少填色”的问题,但是在研究过程中发现了像上面这样,非常多有用的原理和工具。
参考资料
http://en.wikipedia.org/wiki/Graph_theory
http://en.wikipedia.org/wiki/Clique_problem
http://en.wikipedia.org/wiki/NP-complete
仔细想想,交通灯的目的在于什么呢?就是通过引导人们的行动方式防止危险发生,提高安全保障。因此,协调好路口上不同方向间红绿灯的色彩,就成了交通灯设计时要考虑的核心因素。
下面举个具体的例子来说明这个问题,首先我们要建立一些概念;假设有路口如下所示:

这是一个典型的十字路口,我们可以将四条路用方向来命名,上面的叫北路(N),左边的为西路(W);S,E同理。于是上右下左四条路分别为N、E、S、W。
接下来要描述行进方式:如果我们要从北向南行进,我们将之称为N -> S;如果从南路右转弯到东路,则为S -> E;那么从北路过来,左转弯到东路则是N -> E,非常简单。
因此,我们可以知道,对于每一个方向过来的人们,TA们看到的交通灯的颜色,将决定TA们的行动。比如假设有从北向南(即N->S)的人们此时在通行,那么就不能允许由东向西(即E->W)的人通过。因此,在交通灯设计时,我们称N->S与E->W为 “互斥“ 的:
对于互斥的行进方向,交通灯必须显示不同的颜色
因此,根据这个原理,如果N->S通行时,假设用颜色A来表示可通过的状态,这一方向上的人们看到的交通灯颜色则为A;此时E->W方向上的交通灯颜色就应该为颜色B,B表示此时不可通行,总之两个方向上面的交通灯颜色不能一样,否则同时通行的话后果严重。这个很容易理解:北向南行进的人看到的是绿灯的话,东西向的人们肯定看到的红灯。
那么对于由北向南和由南向北的车辆如何呢?N->S和S->N应该是同时被允许的,北向南与南向北通行的人们互不干扰,因为两个方向的人都靠各自的右方通行的话,是不会撞在一起的。因此这两个方向上的人们应该在同一时间段内看到的是同一种颜色的交通灯:它们要么同时可以通行,要么同时需要停下来。
因此设计交通灯时,我们需要考虑的是找出一个路口上面所有的"互斥"状态。比如N->S与E->W是互斥的,它们必须用两种不同的颜色来表示(北向南是绿灯时,东向西必须为红灯)。那么:
到底用多少种颜色,可以将所有的互斥状态标记完全呢?(两种颜色就够吗?)
上面这个问题就是交通灯设计的本质问题。为了解决这个问题,我们首先列出所有可能的行进方向:
N -> W N -> S N -> E E -> N E -> W E -> S S -> W S -> N S -> E W -> N W -> E W -> S
将上面的写法简化一下,便得到了:
NW,NS,NE,EN,EW,ES,SW,SN,SE, WN, WE, WS
如果把上面的几个行进方向变成点,我们就可以得到下面这张图:

从上图中可以看到:
- NW, EN, SE, WS是四种右转弯的情况
- NS,SN,EW,WE四种直行的情况
- SW, ES, NE, WN四个是左转弯的情况
有了这些点以后,将那些互斥的行进方向(也就是上图中的各点)之间连线,所有这些互斥的状态之间便有了线连接。
刚才已经说过,南北通行方为绿灯时,东西方向应该是红灯,那么也就是说:NS,SN,与EW,WE之间是互斥的,于是我们便将NS <--> EW,NS <--> WE,SN <--> EW,SN <--> WE之间连线获得下图:

因为被连线的两个端点看到的信号灯的颜色不能一致,根据这条原则,我们将上图涂色:

仔细看上面这张图:
- 当NS(由(南向北)为红灯时,与它相连的EW(东向西)与WE(西向东)为绿灯
- 当SN(由北向南)为红灯时,与它相连的EW(东向西)与WE(西向东)为绿灯
- NS与SN(北向南与南向北)之间无冲突,没有连线,信号灯颜色一致
- EW与WE(东向西与西向东)之间无冲突,没有连线,信号灯颜色一致
因此,交通灯设计的问题就转化成涂色问题:首先根据事实需要,总结出哪些行进方向之间有冲突,将其转化为点与点之间的连接;然后,这些有冲突的方向的信号灯颜色要设计成不一样,实际上就是为图中所有线两端的点涂上不同的颜色。
上面这个问题是数学里面的一个研究领域,叫做图论。而“用最少的颜色填图”这个细分领域又有它自己的名字,叫做 “NP-complete problems”。这个研究方向一直是数学领域研究的难点,直到现在,人类也并没有找到特别有效的解决办法:基本上现有的方法都可以理解成“把所有的可能都试一遍,两个颜色不成试三个,三个不成试四个。。。”;
用不同的颜色去涂其实并不难,因为我们完全可以用各种各样的颜色,多得用不完。但难就难在如何去证明所用的颜色是最少的。目前数学界还没能完全攻克这个难题,留给后人继续努力。
但这并不是说我们对这类问题束手无策,数学的魅力在于,在研究一个问题的过程中,会产生很多对人类有帮助的工具,而这些工具,本身比证明一个结果更重要。此外,我们在研究这个问题的时间,可能不能完全解决它,但可以部分的解决掉。拿本文的涂色问题来讲,我们现在虽然不能完全的解决掉它,但我们可以对满足一些特殊要求的图有很好的解决方案和工具,在文章的最后部分我会举出一个例子。先回到文本讨论的内容上:
对于十字路口交通信号灯这种比较简单的问题,我们一个一个的用手去填色也花不了多久,只需要把有冲突的点连好线,然后试着用最少的颜色去涂就成了。此外,因为我们已经预先知道答案,红绿两色肯定是够用的,因此解答这个问题本身毫无难度。下面是实际操作的过程:
- 随机找图里面的一个点,如果它和谁都没连线,那肯定是最简单的情况了,不需要涂色(比如右转向都不需要看红绿灯,随时可以右转,当然有的路口特殊,有特别的方向指示交通灯,文章最后会说明,目前不考虑特殊情况)。
- 如果找到的点和别的点之间有连线,那么要判断与它相连的点是否已经被涂色了,如果已经涂了,这个点就要用别的颜色。颜色要从已经用到的里面找,比如和它相连的全部是红色,而和它不相连的点有用绿色的,它就可以用绿色;如果和它相连的点既有红色又有绿色,而图里面还没有用到别的颜色,那么这个点就不得不选一个新的颜色去涂。
不断重复上面的过程,直到所有的点都被涂色,我们就得到了涂好颜色的图。但是有很重要的一点:
这样涂出来的图,用到的颜色不一定是最少的。
还记得我刚才介绍过的吗:去证明用了最少的颜色,是数学难题,你可以花一辈子在研究这个上面。
但是对于本文所讲的这个极其简单的问题,证明起来还是很容易的:因为一条线至少有两个端点,两个端点颜色不能一样,那么至少要用到两种颜色。因此,只要我们只用了两种颜色,那肯定就是最少颜色的情况了。
下面是一个完整的最终涂好颜色的图:

涂色的结果是两种颜色够用了。
接下来我们想想,有没有我们在日常生活中见到的路口,两种颜色的交通灯不够用?其实在大城市的道路上,这种情况还是挺普遍的,比如下面这种左转弯交通灯:

左转弯的时候,要看专门的左转弯灯,直行绿灯放行时,是不可以左转弯的。在这个设计当中,虽然左转弯灯仍然是用绿色表通行,实际上它是红、绿之外的第“三”种颜色。因为单纯靠绿色已经无法区分是直行放行还是左转弯放行了,这个交通灯用“绿色”+“左转弯箭头”的方式,实现了“第三种颜色”。之所以要这样设计,是因为用绿色的附合大众约定俗成的“红灯停,绿灯行”的思维定势,实际上,用别的颜色也可以的,但大部分人可能看不懂信号灯的含义了。
我们要关心的问题是:为什么这种情况下需要第三种颜色呢?还是让我们回到填色图中去找答案,所谓左转弯指示指,实际上等于添加了下面这条限制条件,即:
同方向和垂直方向直行时,不允许左转弯
没有左转弯指示灯的路口,只要直行方向绿灯就可以左转弯的,和垂直方向不冲突;而加上左转弯指示灯,等就是在图中这几个端点之间加了线:
NE <--> NS NE <--> SN ES <--> EW ES <--> WE SW <--> NS SW <--> SN WN <--> EW WN <--> WE
看起来似乎很复杂,但其实这时我们不需要把上面的线全部画出来,就可以判断出此时至少需要三种颜色才够用。为什么?我们可以把以下几条线挑出来:
NS <--> EW NS <--> ES ES <--> EW
在加了左转弯的限制条件后,至少图中有上面三条线,把它画在图里:

会发现,都不必考虑别的线,仅仅是这三个点之间的线,它们两两连通,而我们要想让它们之间的线段两端颜色不同,则至少需要三种颜色:

这就是左转向灯背后的数学原理。从上图中我们可以看中,这三个点之间,两两连通,至少需要3种不同的颜色才可能按要求涂色。这种完全连通的图,在图论里面有一个专门的名词去称呼,叫做"k-clique"。对于"k-clique"图的定义如下:
假设一张图里面有k个点,它们两两之间全部有线连通,我们称之为"k-clique"图。
对于k-clique图,有下述规律:
如果要求"k-clique"图中,线段两端的端点涂不同颜色,则至少需要k种颜色。
因此,对于上面3个点,互相完全连通的图就是一个"3-clique"图,至少需要三种颜色。我们可以看到,虽然图论还未能完全解决“最少填色”的问题,但是在研究过程中发现了像上面这样,非常多有用的原理和工具。
参考资料
http://en.wikipedia.org/wiki/Graph_theory
http://en.wikipedia.org/wiki/Clique_problem
http://en.wikipedia.org/wiki/NP-complete