[转]三维成像原理
http://uh.9ria.com/space-29516-do-blog-id-5510.html
注:网上看到了这样一篇文章写的还是很不错,拿这里给大家分享一下,感谢这位网友不辞辛苦写的这两篇文章,呵呵。本文章转于:DDM君/Furry, Flab3D.com (允许转载,转载请注明)http://hi.baidu.com/sacrtap/blog/item/242fbf516a00ad848d5430db.html
《三维图形成象的基本原理》
一个三维模型/场景要成像和运动在屏幕上,至少需要下面的要素。数学苦手或者完全没接触过的朋友不用怕,了解一下先,具体的计算法我们会在以后的教程中一一说明。
模型和贴图:
三个点连接成一个三角形,很多三角形组成一个模型。
贴图就是模型的每个点(x,y,z)对应的一个平面的(u,v),u,v也就是平面位图的x,y,只不过点用了x,y了,怕重复而已。
Flash3d里面的贴图就是根据每个三角形的不同斜度,和每个点对应的UV计算出beginBitmapFill的第二个矩阵参数(matrix)来用位图填充三角形。
![[转]三维成像原理](http://img.e-com-net.com/image/product/c2ed8569ff724b71956a1f555df9468e.jpg)
运动:
对于初接触图形数学的朋友,下面的道理(二维,三维图形都是这样的道理,只不过三维多一个Z轴)一定会让你吃一惊。
所有我们以为在动的点/模型其实都没有动(相对坐标系),运动的只是坐标系而已。移动,旋转,放大,透视全是同一个原理,不过是在移动,旋转,放大,透视这些点/模型所在的坐标系而已。
所谓摄像机的各种运动根本就是浮云。摄像机绕Y顺时针拍摄,只不过是模型的坐标系在绕Y逆时针转而已。
所有点的任何变动都是一个点(x,y,z)乘以一个矩阵得到的。就这么简单。
千万不要听到这个就吓跑了,我们不需要去仔细研究什么是矩阵,我们只要知道怎么用就行了。而且也根本不需要我们自己去计算,数学算法类flash3d的引擎都是写好了的。
一个东西要动,不管是二维还是三维,就必须得要它的每个点都乘以某个矩阵,这是逃不掉的。
![[转]三维成像原理](http://img.e-com-net.com/image/product/d9776b66610d498f8239cd53a3b2c05c.jpg)
‘投射’在屏幕上
虽说是‘三维’,但实际上我们还是从二维平面的屏幕上观看的。所以我们必须要把三维的点(x,y,z),变成只有(x,y)的点显示在平面的电脑屏幕上。形象一点可以说三维点的显示就是这个点‘投影’在平面的画布上。
有些朋友会说,我直接把x,y,z的z值去掉不就行了。是的,直接去掉我们就能得到一个(x,y)的点,但是这样投影下来图形没有近大远小的变化,看起来稍稍有点奇怪。
于是我们就有了‘透视投影’,算法是用x,y除以某个和Z有关的值w来得到一个近大远小的透视后的(x,y),这才是我们平常看到最正常近大远小的三维图像。
![[转]三维成像原理](http://img.e-com-net.com/image/product/9229ac21203b4153a4d561ac34cf4027.jpg)
图形学的原理是读懂flash3d各种引擎核心内容的基础的基础,只有了解这样的知识后,读引擎源代码才有意义,以后才能慢慢加入写引擎代码的行列,否则只会迷失在代码的海洋中(有时会吐=A=)。 让我们一起迈出这第一步吧,加油!
有任何不清楚的地方,欢迎到讨论区发言。(无需注册)
Matrix3D模型
Matrix3D 类使用一个 4x4 正方形矩阵,即一个由四行和四列数字构成的表,其中容纳了用于转换的数据。矩阵的前三行容纳每个 3D 轴 (x,y,z) 的数据。平移信息位于最后一列中。方向和缩放数据位于前三个列中。缩放因子是位于前三个列中的对角数字。以下是 Matrix3D 元素的表示形式:
![[转]三维成像原理](http://img.e-com-net.com/image/product/d2269daad93c4e97b0cce0698aa880e4.jpg)
空间中的某个点(x,y,z)的任何移动,旋转,缩放的变换,都是用这个点乘以某个一个矩阵而得到。那么模型是由一个个(x,y,z)的点组成,模型整个要变换,就是让每个点乘以某个矩阵。这个我们在《三维成像基本原理里》提到过。
这是三维引擎开发,和引擎代码阅读的必备的基础常识。
Flash3d的引擎里给我们提供了很丰富的运算类。(详细我们在《pv3d, sandy, away3d的三维数学运算类》介绍)
由于(x,y,z)乘以3*3矩阵可以达到旋转和缩放的目的,但是无法表示移动,所以为了统一,我们通常是采用乘以一个4行4列的矩阵。我们flash3d的引擎也都是为我们准备的4*4/4*3矩阵有关的算法。也就是说所有变换方法,都是用如下公式:
变换后点的(x’,y’,z’)=原来的(x,y,z) 乘以 4*4矩阵M
如果使用pv3d的数学类,写法如下:
var 点:number3D=new Number3D(x的值,y的值,z的值); //原来的点
var 数组:Array=[n11,n12,n13, 0,
n21,n22,n23, 0,
n31,n32,n33, 0,
nx , ny, nz, 1]; //构造矩阵内每个值,需要一个数组,我们通常都是以这种格式书写
var 矩阵: Matrix3D=new Matrix3D(数组); //构造矩阵
Matrix3D.multiplyVector4x4(矩阵,点); //点的x,y,z数据直接就更新为相乘后的数据了。
那么具体是用哪个矩阵M呢?下面我们就列出来:
(本教程的公式图,来自Skyman君的博客http://www.cnblogs.com/skyman/)
旋转
旋转在三维里应该是最麻烦的东西,因为人类对旋转的描述是很有限。光靠矩阵控制旋转很多情况是非常复杂和不形象的,所以我们还发明了优拉角和四元数这些对旋转的控制更优良的办法,这些我们以后会讲到。
角度θ表示的是延某轴旋转的角度。
下面三个矩阵分别表示了点绕x轴,y轴,z轴的旋转矩阵。

移动
从公式我们很容易能看出,第4行1,2,3列的数,分别控制着点在x,y,z方向上的移动。

缩放
从公式我们很容易能看出,对角线上的n11,n22,n33,分别控制着点在x,y,z方向上的缩放。
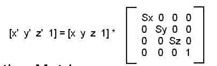
这些就是最简单的变换矩阵,熟悉了这些,我们就又向前迈进了一步。
图形学应该是一个很有趣的东西,并非像很多学校和学生教授的的那种痛苦不堪的东西。其实道理非常简单,如果自己再具备一点编程知识,很容易就能做出自己的成像程序。
注:我把两篇文章放一块了,这样大家理解起来方便,呵呵
注:网上看到了这样一篇文章写的还是很不错,拿这里给大家分享一下,感谢这位网友不辞辛苦写的这两篇文章,呵呵。本文章转于:DDM君/Furry, Flab3D.com (允许转载,转载请注明)http://hi.baidu.com/sacrtap/blog/item/242fbf516a00ad848d5430db.html
《三维图形成象的基本原理》
一个三维模型/场景要成像和运动在屏幕上,至少需要下面的要素。数学苦手或者完全没接触过的朋友不用怕,了解一下先,具体的计算法我们会在以后的教程中一一说明。
模型和贴图:
三个点连接成一个三角形,很多三角形组成一个模型。
贴图就是模型的每个点(x,y,z)对应的一个平面的(u,v),u,v也就是平面位图的x,y,只不过点用了x,y了,怕重复而已。
Flash3d里面的贴图就是根据每个三角形的不同斜度,和每个点对应的UV计算出beginBitmapFill的第二个矩阵参数(matrix)来用位图填充三角形。
![[转]三维成像原理](http://img.e-com-net.com/image/product/c2ed8569ff724b71956a1f555df9468e.jpg)
运动:
对于初接触图形数学的朋友,下面的道理(二维,三维图形都是这样的道理,只不过三维多一个Z轴)一定会让你吃一惊。
所有我们以为在动的点/模型其实都没有动(相对坐标系),运动的只是坐标系而已。移动,旋转,放大,透视全是同一个原理,不过是在移动,旋转,放大,透视这些点/模型所在的坐标系而已。
所谓摄像机的各种运动根本就是浮云。摄像机绕Y顺时针拍摄,只不过是模型的坐标系在绕Y逆时针转而已。
所有点的任何变动都是一个点(x,y,z)乘以一个矩阵得到的。就这么简单。
千万不要听到这个就吓跑了,我们不需要去仔细研究什么是矩阵,我们只要知道怎么用就行了。而且也根本不需要我们自己去计算,数学算法类flash3d的引擎都是写好了的。
一个东西要动,不管是二维还是三维,就必须得要它的每个点都乘以某个矩阵,这是逃不掉的。
![[转]三维成像原理](http://img.e-com-net.com/image/product/d9776b66610d498f8239cd53a3b2c05c.jpg)
‘投射’在屏幕上
虽说是‘三维’,但实际上我们还是从二维平面的屏幕上观看的。所以我们必须要把三维的点(x,y,z),变成只有(x,y)的点显示在平面的电脑屏幕上。形象一点可以说三维点的显示就是这个点‘投影’在平面的画布上。
有些朋友会说,我直接把x,y,z的z值去掉不就行了。是的,直接去掉我们就能得到一个(x,y)的点,但是这样投影下来图形没有近大远小的变化,看起来稍稍有点奇怪。
于是我们就有了‘透视投影’,算法是用x,y除以某个和Z有关的值w来得到一个近大远小的透视后的(x,y),这才是我们平常看到最正常近大远小的三维图像。
![[转]三维成像原理](http://img.e-com-net.com/image/product/9229ac21203b4153a4d561ac34cf4027.jpg)
图形学的原理是读懂flash3d各种引擎核心内容的基础的基础,只有了解这样的知识后,读引擎源代码才有意义,以后才能慢慢加入写引擎代码的行列,否则只会迷失在代码的海洋中(有时会吐=A=)。 让我们一起迈出这第一步吧,加油!
有任何不清楚的地方,欢迎到讨论区发言。(无需注册)
Matrix3D模型
Matrix3D 类使用一个 4x4 正方形矩阵,即一个由四行和四列数字构成的表,其中容纳了用于转换的数据。矩阵的前三行容纳每个 3D 轴 (x,y,z) 的数据。平移信息位于最后一列中。方向和缩放数据位于前三个列中。缩放因子是位于前三个列中的对角数字。以下是 Matrix3D 元素的表示形式:
![[转]三维成像原理](http://img.e-com-net.com/image/product/d2269daad93c4e97b0cce0698aa880e4.jpg)
空间中的某个点(x,y,z)的任何移动,旋转,缩放的变换,都是用这个点乘以某个一个矩阵而得到。那么模型是由一个个(x,y,z)的点组成,模型整个要变换,就是让每个点乘以某个矩阵。这个我们在《三维成像基本原理里》提到过。
这是三维引擎开发,和引擎代码阅读的必备的基础常识。
Flash3d的引擎里给我们提供了很丰富的运算类。(详细我们在《pv3d, sandy, away3d的三维数学运算类》介绍)
由于(x,y,z)乘以3*3矩阵可以达到旋转和缩放的目的,但是无法表示移动,所以为了统一,我们通常是采用乘以一个4行4列的矩阵。我们flash3d的引擎也都是为我们准备的4*4/4*3矩阵有关的算法。也就是说所有变换方法,都是用如下公式:
变换后点的(x’,y’,z’)=原来的(x,y,z) 乘以 4*4矩阵M
如果使用pv3d的数学类,写法如下:
var 点:number3D=new Number3D(x的值,y的值,z的值); //原来的点
var 数组:Array=[n11,n12,n13, 0,
n21,n22,n23, 0,
n31,n32,n33, 0,
nx , ny, nz, 1]; //构造矩阵内每个值,需要一个数组,我们通常都是以这种格式书写
var 矩阵: Matrix3D=new Matrix3D(数组); //构造矩阵
Matrix3D.multiplyVector4x4(矩阵,点); //点的x,y,z数据直接就更新为相乘后的数据了。
那么具体是用哪个矩阵M呢?下面我们就列出来:
(本教程的公式图,来自Skyman君的博客http://www.cnblogs.com/skyman/)
旋转
旋转在三维里应该是最麻烦的东西,因为人类对旋转的描述是很有限。光靠矩阵控制旋转很多情况是非常复杂和不形象的,所以我们还发明了优拉角和四元数这些对旋转的控制更优良的办法,这些我们以后会讲到。
角度θ表示的是延某轴旋转的角度。
下面三个矩阵分别表示了点绕x轴,y轴,z轴的旋转矩阵。

移动
从公式我们很容易能看出,第4行1,2,3列的数,分别控制着点在x,y,z方向上的移动。

缩放
从公式我们很容易能看出,对角线上的n11,n22,n33,分别控制着点在x,y,z方向上的缩放。
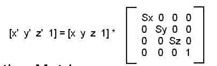
这些就是最简单的变换矩阵,熟悉了这些,我们就又向前迈进了一步。
图形学应该是一个很有趣的东西,并非像很多学校和学生教授的的那种痛苦不堪的东西。其实道理非常简单,如果自己再具备一点编程知识,很容易就能做出自己的成像程序。
注:我把两篇文章放一块了,这样大家理解起来方便,呵呵