counting sort和radix sort

简介

    counting sort和radix sort和原来的那些通过比较交换来排序的方法不一样。原来的常用排序算法比如插入排序，快速排序等都通过交换元素和递归等手段。而counting sort和radix sort都采用一种类似于映射的方式来实现排序的效果。当然，这种方式之所以会达到O(n)的量级，主要的原因在于这些个排序算法有一个限制，就是首先他们数据的取值范围是在[0, k]，数据的个数为n，且n >= k。

counting sort 

推导思路

    counting sort的过程是基于一个很直观的思考。在前面提到过，我们有n个元素，所有元素的取值范围在[0, k]这个区间。那么，假设我们有一个数组b，它的长度为k的话，那么对于数组中间的任意一个元素i，它在排序后的位置肯定就映射到b[i]的这个点上。只是可能有多个重复的值对应到同一个点。取一个最特殊的情况，假设我们正好也是有k个元素，而且每个元素也都仅出现一次。那么，按照我们这个映射的思路，每个元素放到对应数组索引的位置，排序的结果就生成了。

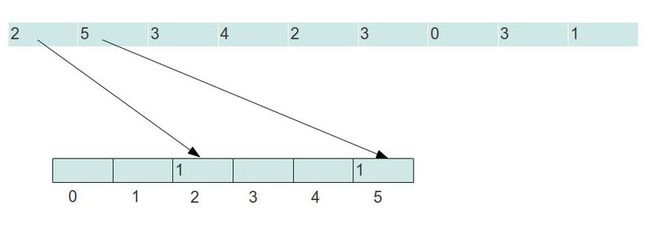
    再在我们前面说的这个特殊情况的基础上考虑让它更加通用化一点。前面的直接映射是在于每个值都只出现唯一一次。而实际上可能有一个数字出现了若干次而有的数字完全没有出现过。但是，不管它出现没出现，他们所有的值的范围是在[0, k]之间。那么，如果我们定义一个b[k]这样的数组来映射，如果某个元素i出现的次数多于一次的话，我们可以将它出现的次数设置为b[i]的数值。如下图所示：

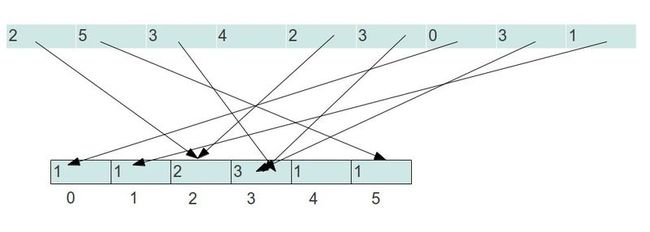
    这样，我们这个数组里就保存了一个所有元素映射后的结果。只不过有的点是对应了多个同样的值。如果这个时候再返回所有排序后的结果，相信只要通过一个循环，从最小到最大。碰到b[i]值为0的则表示没有，直接跳过。大于0的表示出现了多个，就重复输出多个i。那么，这个映射的方法也就出来了。最终映射的结果如下图：

    通过前面的讨论，我们可以得出如下的代码：

public static void countingSort(int[] a, int[] b, int k)
{
	int[] c = new int[k];
	for(int i = 0; i < a.length; i++)
		c[a[i]] = c[a[i]] + 1;
	int count = 0;
	for(int j = 0; j < c.length; j++)
	{
		while(c[j] > 0)
		{
			b[count++] = j;
			c[j]--;
		}
	}
}

    这是一种通过记录结果然后重新构造的方式来返回结果。当然，我们也可以直接返回数组b。

    嗯.....慢着慢着。如果你看过书上counting sort的代码的话，你会发现，这和书上说的完全不一样啊。虽然实际的实现方式有点差别，实际上，我们这种方法和书上的思路是一样的。现在我们再来看看书上的写法吧。

书上说

    书上说的counting sort大致是分为三个步骤。1. 统计数字的映射，和我们前面的方法一样。 2. 对数组进行累加，每个元素表示原来数组中从开头到当前元素的和。3. 再根据原来的数组来映射出新的排序后的结果。说到这里，大家可能对第2，3步还是不太清楚。没关系，我们一点点的来看。

    首先，按照原来的统计方式，我们可以得到一个统计结果的数组。以原来的数据为例，我们可以通过如下代码：

for(int i = 0; i < a.length; i++)
	c[a[i]] = c[a[i]] + 1;

 得到一个结果数组，如下图：

    然后，我们再通过如下的代码，进行累加：

for(int i = 1; i < k; i++)
	c[i] = c[i] + c[i - 1];

 这样，我们可以得到一个如下的数组：

 

    我们来看这么一个累加的步骤的意义。每次我们将当前的元素加上前面的元素时，前面的元素表示从最开始元素到当前元素的累加。那么对于结果数组中的任一元素i，c[i]表示从c[0]到c[i]之间所有元素的和。再看我们前面定义的这个数组的含义。它本身是用来保存当前值为i的元素的个数的。那么c[i]则表示从0到i的所有元素的总和。再换一个角度来想想，既然c[i]表示最大值为i的所有元素个数，那么如果有i这么一个元素的话，它最大的索引就是c[i]。

    那么，有没有这个元素i呢？这就要看我们的源数组了，假定为a[i]。对于每个存在的元素a[i]，我们可以发现它对应的最大索引则为c[a[i]]。然后，再考虑到我们有元素重复的情况，我们可以在每次找到一个对应的c[a[i]]的情况下，把c[a[i]]减一。这相当于我们已经取了这个元素i之后，保证剩下元素的正确性。那么，这几个操作就是我们讲到的第三步。它对应实现的代码如下：

for(int j = a.length; j >= 0; j--)
{
	b[c[a[j]] - 1] = a[j];
	c[a[j]]--;
}

 将我们前面的这几个步骤统一一下，couting sort在书面上定义的一个完整实现方法如下：

 

public static void countingSort(int[] a, int[] b, int k)
{
	int[] c = new int[k];
		
	for(int i = 0; i < a.length; i++)
		c[a[i]] = c[a[i]] + 1;
	for(int i = 1; i < k; i++)
		c[i] = c[i] + c[i - 1];
	for(int j = a.length; j >= 0; j--)
	{
		b[c[a[j]] - 1] = a[j];
		c[a[j]]--;
	}
}

    在实际实现中，考虑到我们要用到的数组是从0开始索引的，所以后面第三步映射的时候结果数组b对应的值要减一。

radix sort

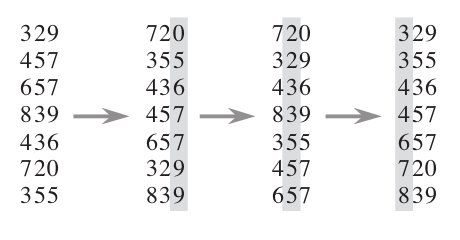
    radix sort是一个看起来很好理解，实现起来还是有点麻烦的方法。它也有一个强烈的前置依赖条件。就是我要排序的数据具有相同的位数。比如说，我所有的数据都是3位数或者4位数的。然后我们对所有数据从最小一位到最大的位开始排序。下图展示了一个radix sort的流程：

 

    从本身radix sort的定义来看，我们发现他们有一个有意思的特性。对于n个元素，它们对应的每一位的值的范围都是在[0，9] 之间的。没想到，这倒是一个很符合前面counting sort要求的条件。那么，就上counting sort吧。我们将他们每一位按照counting sort排序，这样得到的最后结果就是radix sort了。

    当然，这里有一个和纯counting sort不一样的地方。原来每次排序我们是针对整个数字，这次只是针对数字的一个位。每次映射的时候就需要注意这么一个对应的关系。

    另外，还有一个需要考虑的就是每次取数据中间的某一位。我们可以通过不断整除的方式来求。这个得出某一位数字的方法如下：

public static int getNthDigit(int value, int n)
{
	for(int i = 0; i < n; i++)
	{
		value /= 10;
	}

	return value % 10;
}

     在将前面的几部分整合起来，也不难得出radix sort剩下的部分了：

public static int[] radixSort(int[] a, int bitCount)
{
	int[] c;
	int[] b = new int[a.length];
	for(int k = 0; k < bitCount; k++)
	{
		c = new int[10];
		for(int i = 0; i < a.length; i++)
		{
			int nThDigit = getNthDigit(a[i], k);
			c[nThDigit] = c[nThDigit] + 1;
		}
		for(int i = 1; i < c.length; i++)
			c[i] = c[i] + c[i - 1];
			
		for(int j = a.length - 1; j >= 0; j--)
		{
			int bitDigit = getNthDigit(a[j], k);
			b[c[bitDigit] - 1] = a[j];
			c[bitDigit]--;
		}
			
		for(int i = 0; i < b.length; i++)
			a[i] = b[i];
	}

	return b;
}

 

总结

    counting sort的本质无非是利用数字范围的有限性然后进行映射计数。它能够高效运行的一个前提是他们元素的取值范围不大。它的时间复杂度为O(n)。因为要考虑结果的映射和拷贝，空间复杂度为O(n + k)。假定k是所有元素的取值范围。radix sort有一个要求是所有比较元素长度要一样，他们可以按位进行比较排序。它的时间复杂度为O(nk)。假设k为元素的位数。counting sort和radix sort都是稳定的排序算法。 

 

参考材料

 Introduction to algorithms