Horspool和Sunday
目的:
以Horspool和Sunday算法为载体,试图在减少思维断层情况下学习作者算法思想
目录:
1:Horspool算法:简单的力量
2:Horspool代码实现
3:Sunday算法过程
4:Sunday代码实现
5:重新半理性审视BF、KMP、BM、Horspool和Sunday。(关键)
1:Horspool算法过程:简单的力量
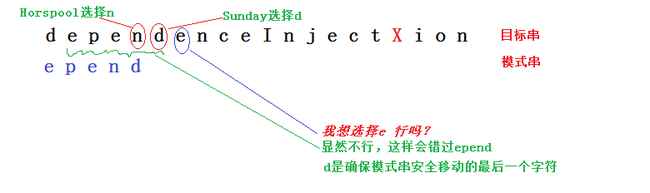
Horspool算法的思路非常简单。它是对BM算法的一个简化。在BM中,作者使用了两种启发性规则即:坏字符规则和好后缀规则。Horspool认为,在某个字符匹配失败的情况下,挑选最后一个字符应用坏字符规则总是能够产生最大的跳跃距离。
过程阐述:
Horspool算法从右向左对字符匹配,如果最后一个字符相同,则匹配下一个字符,直到所有字符相同或者某一个字符不同;无论匹配成功与否,都根据最后一个字符进行在模式串中出现的位置进行移动。
如图:

所以Horspool算法只设计了一个shift算法来计算匹配失败的时候移动距离。
根据模式串,初始化一个数组。数组中保存的是该字符距离末位的距离。
之后从后向前开始匹配,匹配失败则从数组中取出对应移动距离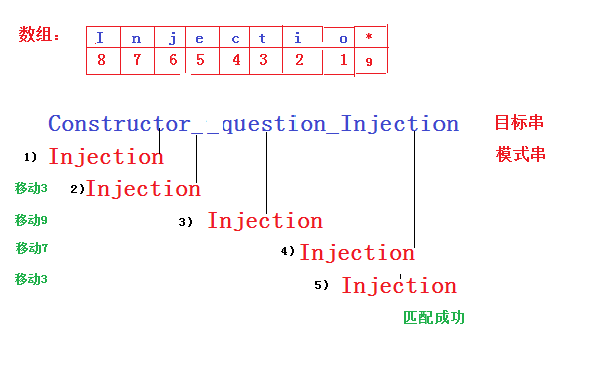
2:Horspool代码实现
public static int horspool(String target,String pattern){
//预处理
int skip []= precessChars(pattern);
//
int lengthMinusOne = pattern.length()-1;
int i,j,k;
for(k = lengthMinusOne;k<target.length();k+=skip[target.charAt(k)]){
//j>=0&&target.charAt(i)==pattern.charAt(j) 顺序不能改变 否则报数组越界
for(i=k,j=lengthMinusOne;j>=0&&target.charAt(i)==pattern.charAt(j);--j,--i){
//空
}
if(j == -1){
return i+1;
}
}
return -1;
}
private static int[] precessChars(String pattern){
final int count = 256;
int [] skip = new int[count];
for(int j=0;j<count;j++){
skip[j] = pattern.length();
}
//遍历到pattern.length()-1 不包含最后一个字符
for(int i =0;i<pattern.length()-1;i++){
char c = pattern.charAt(i);
skip[c]=pattern.length()-1-i;
}
return skip;
}
3:Sunday算法
其实Sunday算法也是BM算法的一个简化,和Horspool很是相像。差别在于当匹配失败的时候,Sunday算法选取的是最后一个字符的下一个字符进行匹配。但是Sunday算法并不要求匹配的时候从前到后或者是从后到前,甚至可以从中间开始匹配。 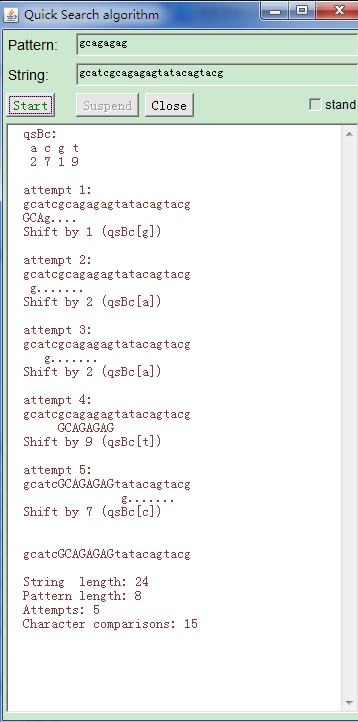
4:Sunday代码实现
//从后向前
public static int sunday_back(String target,String pattern){
//预处理
int skip []= precessChars(pattern);
//
int length = pattern.length();
int i,j,k;
for(k = length;k<=target.length();k+=skip[target.charAt(k)]){
for(i=k-1,j=length-1;j>=0&&target.charAt(i)==pattern.charAt(j);--j,--i){
//空
}
if(j == -1){
return i+1;
}
}
return -1;
}
//从前向后
public static int sunday_forward(String target,String pattern){
//预处理
int skip []= precessChars(pattern);
//
int length = pattern.length();
int i,j,k;
for(k = length;k<=target.length();k+=skip[target.charAt(k)]){
for(i=k-length,j=0;j<length&&target.charAt(i)==pattern.charAt(j);j++,i++){
//空
}
if(j == length){
return k-length;
}
}
return -1;
}
//预处理数组
private static int[] precessChars(String pattern){
final int count = 256;
int [] skip = new int[count];
for(int j=0;j<count;j++){
skip[j] = pattern.length();
}
//遍历到pattern.length()-1 不包含最后一个字符
for(int i =0;i<pattern.length()-1;i++){
char c = pattern.charAt(i);
skip[c]=pattern.length()-i;
}
return skip;
}
关于Sunday和Horspool算法,两者到底有多少差别,其实很难做出比较。一般来讲,Sunday算法能带来更大的平均移动距离。但是至于谁更快一些,可能涉及到内存引用次数等问题,需要大量的实验。
5:重新审视BF、KMP、BM、Horspool和Sunday。
当匹配失败的时候,到底怎么样才能跳跃式前进的距离最远呢?其实经过对Horspool和Sunday的分析,会得到一些启发。
Horspool中取当前字符中最后一个进行移位;Sunday算法选择最后一个字符的后一个进行移位。
启示1:既然Sunday选取最后一个的下一位,平均移位距离有所增加,何不选择最后一个的下两位呢?
启示2:何不综合Sunday和Horspool算法,将每次移位前取两者进行比较后更大者移动呢?
对于启示1,可以这样考虑,如果能够无限制的选取下一位,如果目标串中有个模式串中没有的字符X,岂不是就可以直接跳过X了?
对于启示2,实际上也是BF、KMP、和BM算法的差异所在之处。
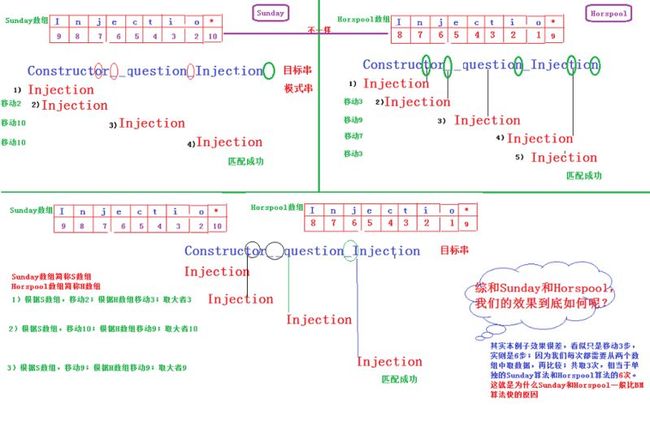
通过上图比较,我们可以看出,如果综合Sunday算法和Horspool算法来考虑,效率不一定高,因为每次都将两者数组取出来的值比较一次,还不如就按照其中一个算法进行,这个时间内可能已经又向前迈进了一大步。
其实总和Sunday和Horspool的想法并没有错,我们最好的情况下就是将每个字符要移动的情况下都计算出来,取最大的(有点贪婪),但是就是在你根据不同字符计算需要移动的位置的时候,已经花费的大把大把的时间,可能Sunday算法已经执行完毕。所以我们要做的是在最少的时间内将获得的信息发挥最大的价值。
于是BF是怎么做的,简单的根据第一个字符进行移动;而KMP是根据已经匹配的字符的最大前缀(和该最大前缀相同的后缀是最靠近匹配失败的字符的)移动,如果符合KMP要求的后缀是多个字符,实际上相当于我们的启示2,比较了多个字符取其大,这个时候利用了预处理数组next,可以在o(1)时间内完成,是很有效果的。KMP实际可以稍微改动一下,并不利用已经匹配的字符,只是根据匹配失败的字符移动,相信效率会有所提升。再到后来的BM算法,终于发现了后缀匹配,但是BM算法还只是在利用坏字符规则的时候是根据匹配失败字符移动,好后缀规则实则起不到太大的作用,只是一个配角。然后Horspool彻底的摒弃了好后缀规则,就像我们曾经根据启示2试图总和Sunday和Horspool一样,Horspool没有这样做,而是选取了好后缀规则和坏字符规则中的一个即坏字符规则,这样做思路反而变得简单,收到的效果也还比BM好很多。而至于Sunday算法,做的更绝,直接选择最后一个字符的下一个字符,这个是能够选得最后一个字符了。用图片表示:
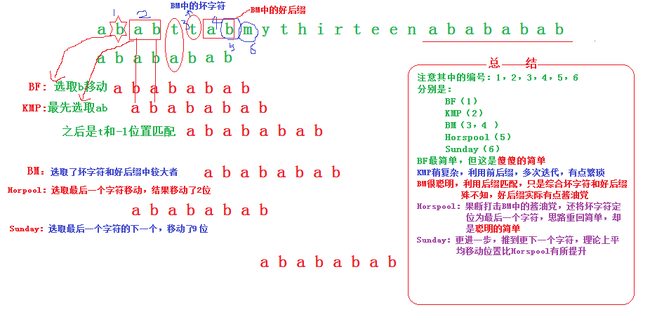
其实大量的信息都是在自己画的图上,能够半理性的展示这些算法的思想。