A*寻路 -- 更加真实 的路径(一)
转:http://bbs.9ria.com/thread-86464-2-1.html
对于A*寻路算法,可能是游戏开发者讨论最多的话题之一,很多游戏都会用到它来实现游戏角色的寻路。那么我这篇帖子的价值何在呢?先来看看传统A*算法存在的问题:
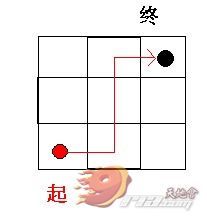
1.尴尬的Z型路径
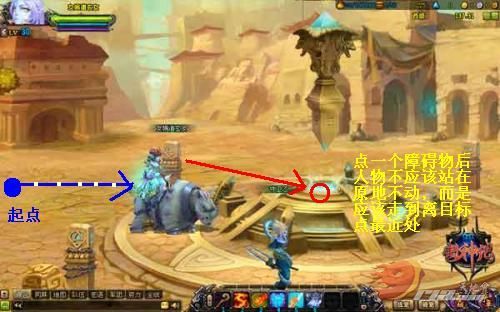
当你在用A*算法实现了角色行走逻辑后,点击一个目标点,虽然你起点和目标点间没有任何障碍物,但角色还TMD蛋疼地进行了Z型行走路线,拐了好多次弯,他丫的那么风骚的走位,以为有人在用狙击枪——瞄准他呢!?
2.无路可走
当你使用A*算法的时候你可能会发现,当你选择一个不可移动点或者一个被障碍物围住的“岛屿”点作为目标点的时候A*寻路算法会返回false的寻 路结果,通知你它没有找到一条通路,那么此时你怎么办?角色只能站在原地干瞪眼,用户见状可能还以为自己鼠标失灵了呢。“咦?我明明点了那里,这角色咋不 动捏?shit~!”
3.效率不高
你可能在网上或者书籍(如《ActionScript3 动画高级编程》)附赠光盘中下载过A*寻路源码,但运行后发现寻路一次会耗费10毫秒以上,有时候点击一个不可移动点或者一个封闭区域时更会耗费上百毫秒 (因为此时A*算法会遍历全部的格子直至最终无法找到路径)。
这些问题相信很多A*算法使用者都遇到过,但是有一些人因为水平不足,无法继续深究下去,而且网上对此问题的解决方案也是没有任何参考资料可循。另一部 分高手已找到解决之道,但是不愿意开源,以至于那么多年来网上依然缺乏对A*算法这些不足之处的解决之道。其实有时候想想,游戏公司的策划也蛮可怜的,他 的想法很不错,但是程序员往往会以一句“没办法解决”或者“实现不了”就给浇了冷水,唉,可能这也是国内缺乏优秀游戏的原因之一吧。
那么,废话少说,马上开始我们的讲解吧,希望我这篇帖子能给一些迷途的道友们指引一下方向。
更合理的行走方式
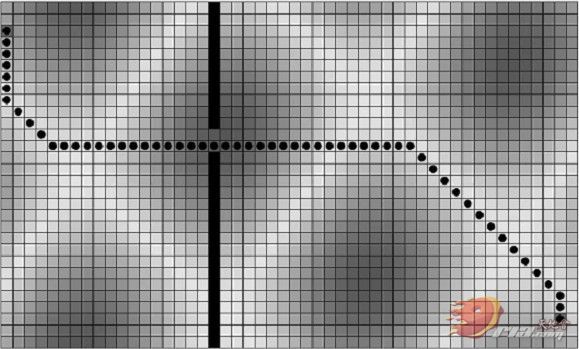
对于第一个问题,可以用下图来解释这一现象,当我们选择一个目标点后,即使目标点与起始点间无障碍物存在,A*寻路产生的路径依然是曲折的:
这是由于A*寻路算法是基于格子进行寻路的,因此返回的寻路结果将是一个包含很多格子对象(假设格子对象的类名为Node)的数组,那么在行走的过程中 自然是根据“到达路径数组中一个Node对象的屏幕坐标所在处之后以数组中下一个Node对象的屏幕坐标所在处为下一个目的地”这样的行走过程进行行走 的.
那么如何避免这种情况的发生呢?我想只在必要的时候调用A*寻路行不行呢?当终点与起点间无任何障碍物的时候直线行走,有障碍物了再进行寻路行走,如下图所示: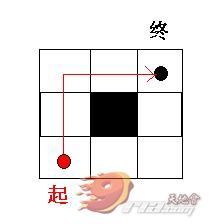
有想法就有可能,impossible is nothing!
首先要解决的问题是如何判断起点和终点间是否存在障碍物,如果你还记得初中数学中“直线”这一章的内容(很多人看到这里估计要骂一句“holy shit”)的话应该不难想到利用直线的数学特性来解决这一难题。什么?你数学学的东西全TMD忘光了?好吧好吧,还是让贫道来指引一下吧……
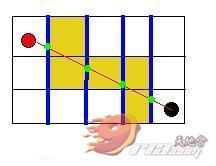
先看到下图,我们把两点的中心点用直线连接起来,直线经过的格子都以屎黄色标示(我就喜欢屎黄色),当然,不包含这两个当事点^_^
此时我们就可以依次检查这些大便节点(即用屎黄色填充的点)中是否有一个是障碍点,若有任意一个是障碍点,那么就表示着我这两个当事点之间走直线是行不通地!
说着简单吧?那就做着吧……可是……用代码怎么写啊?说到这,我当初也确实被难住了,用代码实现这一数学思想的确有些困难,那么,我们一步步来吧。
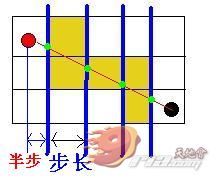
首先我们要想正确地用代码获知这些大便节点并非易事,我首先想到的方案是以一个节点宽度为步长,从起点到终点横向遍历出它们之间连线(假设此连线叫 l )与每个节点左边缘的交点,见下图:
图上绿色的点就是我们第一步需要求得的线段 l 与起点终点间所有节点的交点了,从图上我们发觉,由于 l 是起点与终点节点中心点的连线,所以第一次遍历时取的步长是半个节点宽,之后遍历的步长则是一个节点宽了。那么求得这些点有什么用呢?从图上看到,只要正 确地得到了这些关键点,之后就可以求每个关键点所毗邻的全部节点以最终得到全部的大便节点,如上图中最左边这个绿色的关键点它所毗邻的两个节点是起点(红 色圆球所在点)以及起点右边那个(1,0)号点。由此,我们可以先把循环体给定下来了,如果假设我们用来计算两点间是否存在障碍物的方法名叫做 hasBarrier,那么它的代码雏形如下:
/**
* 判断两节点之间是否存在障碍物
*
*/
public function hasBarrier( startX:int, startY:int, endX:int, endY:int ):Boolean
{
//为了运算方便,以下运算全部假设格子尺寸为1,格子坐标就等于它们的行、列号
/** 循环递增量 */
var i:Number;
/** 循环起始值 */
var loopStart:Number;
/** 循环终结值 */
var loopEnd:Number;
loopStart = Math.min( startX, endX );
loopEnd = Math.max( startX, endX );
//开始横向遍历起点与终点间的节点看是否存在障碍(不可移动点)
for( i=loopStart; i<=loopEnd; i++ )
{
//由于线段方程是根据终起点中心点连线算出的,所以对于起始点来说需要根据其中心点
//位置来算,而对于其他点则根据左上角来算
if( i==loopStart )i += .5;
............
if( i == loopStart + .5 )i -= .5;
}
}
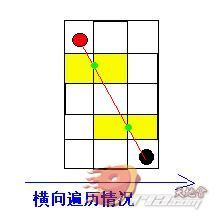
但是这样根据x值横向遍历会不会漏掉一些节点呢?答案是肯定的,看下图这种情况
按上面我所说的横向遍历的规则,第一次遍历我求得了上图左边这个绿色点,第二次遍历求得了右边这个绿色点,在求得此二关键点后求出它们各自所毗邻的节点并在图上以屎黄色标示,发现遍历结果中漏掉了中间这块节点。
那么咋办呢?细心的道友会提出一个方案:对 l 倾斜角大于45度角的情况(此时起点与终点间纵向距离大于横向距离)使用纵向遍历,而对倾斜角小于45度 的情况(此时起点与终点间横向距离大于纵向距离)使用横向遍历,这样就不会漏掉任何一个大便点了。没有错,答案就是如此,奖励这位回答正确的同学一只小红 花,哦不,还是奖励小菊花吧~再回头看看刚才那个漏掉大便点的情况,那时 l 倾斜角已大于45度,因此采用纵向遍历,结果如下:
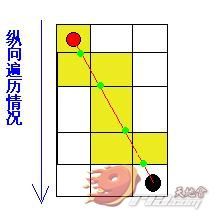
oh, yeah, perfect!
既然遍历的方向要根据情况而定,所以原先代码将更改为下面这样:
//根据起点终点间横纵向距离的大小来判断遍历方向
var distX:Number = Math.abs(endX - startX);
var distY:Number = Math.abs(endY - startY);
/**遍历方向,为true则为横向遍历,否则为纵向遍历*/
var loopDirection:Boolean = distX > distY ? true : false;
/** 循环递增量 */
var i:Number;
/** 循环起始值 */
var loopStart:Number;
/** 循环终结值 */
var loopEnd:Number;
//为了运算方便,以下运算全部假设格子尺寸为1,格子坐标就等于它们的行、列号
if( loopDirection )
{
loopStart = Math.min( startX, endX );
loopEnd = Math.max( startX, endX );
//开始横向遍历起点与终点间的节点看是否存在障碍(不可移动点)
for( i=loopStart; i<=loopEnd; i++ )
{
//由于线段方程是根据终起点中心点连线算出的,所以对于起始点来说需要根据其中心点
//位置来算,而对于其他点则根据左上角来算
if( i==loopStart )i += .5;
…………
if( i == loopStart + .5 )i -= .5;
}
}
else
{
loopStart = Math.min( startY, endY );
loopEnd = Math.max( startY, endY );
//开始纵向遍历起点与终点间的节点看是否存在障碍(不可移动点)
for( i=loopStart; i<=loopEnd; i++ )
{
if( i==loopStart )i += .5;
…………
if( i == loopStart + .5 )i -= .5;
}
}
好了,接下来该做的就是决定循环体中应该执行的逻辑了。前面寡人说过,我们的最终目的是得到线段 l 经过的大便点,那么要得到这些大便点就必须先求得那些绿色的关键点才行。现在我们已经知道了遍历的规则,可能是横向遍历也可能是纵向遍历,假设我们使用横 向遍历的情况下,再假设每个格子的尺寸都是1,那么这些绿色关键点的 x 值就都是已知的了。
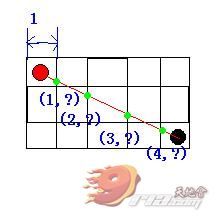
要求得绿点的 y 值,只需要将它们的 x 值代入线段 l 的直线方程(假设直线方程为 y = ax + b )中即可。所以接下来要做的事情就是先求出这个直线方程中的未知数 a 与 b 的值。
既然我们已知了该线段两段的端点坐标,把它们的坐标值代入方程即可求得未知数 a 与 b。我把这一数学求解方程的代码放在一个数学类MathUtil.as中,代码如下:
package
{
import flash.geom.Point;
/**
* 寻路算法中使用到的数学方法
* @author Wangzhouquan
*
*/
public class MathUtil
{
/**
* 根据两点确定这两点连线的二元一次方程 y = ax + b或者 x = ay + b
* @param ponit1
* @param point2
* @param type 指定返回函数的形式。为0则根据x值得到y,为1则根据y得到x
*
* @return 由参数中两点确定的直线的二元一次函数
*/
public static function getLineFunc(ponit1:Point, point2:Point, type:int=0):Function
{
var resultFuc:Function;
// 先考虑两点在一条垂直于坐标轴直线的情况,此时直线方程为 y = a 或者 x = a 的形式
if( ponit1.x == point2.x )
{
if( type == 0 )
{
throw new Error("两点所确定直线垂直于y轴,不能根据x值得到y值");
}
else if( type == 1 )
{
resultFuc = function( y:Number ):Number
{
return ponit1.x;
}
}
return resultFuc;
}
else if( ponit1.y == point2.y )
{
if( type == 0 )
{
resultFuc = function( x:Number ):Number
{
return ponit1.y;
}
}
else if( type == 1 )
{
throw new Error("两点所确定直线垂直于y轴,不能根据x值得到y值");
}
return resultFuc;
}
// 当两点确定直线不垂直于坐标轴时直线方程设为 y = ax + b
var a:Number;
// 根据
// y1 = ax1 + b
// y2 = ax2 + b
// 上下两式相减消去b, 得到 a = ( y1 - y2 ) / ( x1 - x2 )
a = (ponit1.y - point2.y) / (ponit1.x - point2.x);
var b:Number;
//将a的值代入任一方程式即可得到b
b = ponit1.y - a * ponit1.x;
//把a,b值代入即可得到结果函数
if( type == 0 )
{
resultFuc = function( x:Number ):Number
{
return a * x + b;
}
}
else if( type == 1 )
{
resultFuc = function( y:Number ):Number
{
return (y - b) / a;
}
}
return resultFuc;
}
}
}
这个方法将会根据两个参数点求得它们连线的直线方程并返回一个函数实例,如果你第三个参数type传入的是0,那么将会得到一个类似于 y = ax + b这样的函数实例,假设此实例名为fuc,那么你可以传一个 x 值作为 fuc 的参数,它会返回给你一个在直线 l 上横坐标等于此 x 值的点的 纵坐标 y = fuc( x ); 如果你第三个参数传入的是1,那么将会得到一个类似于 x = ay + b这样的函数实例,可以根据你传入的 y 值得到直线 l 上纵坐标为 y 的点的横坐标 x = fuc( y )。 设置type这样一个参数是因为我们可能横向遍历也可能纵向遍历,横向遍历时我需要根据 x 值来求 y,纵向遍历时则相反。
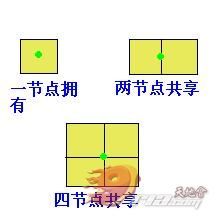
好了,有了这个方法以后我们要求出绿色的关键点应该是没有问题了,接下来要做的就是根据一个关键点求出它所毗邻的节点有几个,它们分别是哪些。一般来说,最多可能有4个节点共享一个关键点,最少则是一个节点拥有一个关键点:
如果假设一个节点的宽、高均为1,那么如果一个点的 x 、y 值都不是整数那就可以判定它只可能由一个节点拥有;如果 x 值为整数则表示此点会落在两个节点横向的临边上;如果 y 值为整数则表示此点会落在两个节点纵向的临边上。由此可得getNodesUnderPoint方法:
/**
* 得到一个点下的所有节点
* @param xPos 点的横向位置
* @param yPos 点的纵向位置
* @param exception 例外格,若其值不为空,则在得到一个点下的所有节点后会排除这些例外格
* @return 共享此点的所有节点
*
*/
public function getNodesUnderPoint( xPos:Number, yPos:Number, exception:Array=null ):Array
{
var result:Array = [];
var xIsInt:Boolean = xPos % 1 == 0;
var yIsInt:Boolean = yPos % 1 == 0;
//点由四节点共享情况
if( xIsInt && yIsInt )
{
result[0] = getNode( xPos - 1, yPos - 1);
result[1] = getNode( xPos, yPos - 1);
result[2] = getNode( xPos - 1, yPos);
result[3] = getNode( xPos, yPos);
}
//点由2节点共享情况
//点落在两节点左右临边上
else if( xIsInt && !yIsInt )
{
result[0] = getNode( xPos - 1, int(yPos) );
result[1] = getNode( xPos, int(yPos) );
}
//点落在两节点上下临边上
else if( !xIsInt && yIsInt )
{
result[0] = getNode( int(xPos), yPos - 1 );
result[1] = getNode( int(xPos), yPos );
}
//点由一节点独享情况
else
{
result[0] = getNode( int(xPos), int(yPos) );
}
//在返回结果前检查结果中是否包含例外点,若包含则排除掉
if( exception && exception.length > 0 )
{
for( var i:int=0; i<result.length; i++ )
{
if( exception.indexOf(result[i]) != -1 )
{
result.splice(i, 1);
i--;
}
}
}
return result;
}
万事具备,只欠东风了,最后把之前写的两个方法用到hasBarrier方法的循环体中去。下面是完整的hasBarrier方法代码:
/**
* 判断两节点之间是否存在障碍物
*
*/
public function hasBarrier( startX:int, startY:int, endX:int, endY:int ):Boolean
{
//如果起点终点是同一个点那傻子都知道它们间是没有障碍物的
if( startX == endX && startY == endY )return false;
//两节点中心位置
var point1:Point = new Point( startX + 0.5, startY + 0.5 );
var point2:Point = new Point( endX + 0.5, endY + 0.5 );
//根据起点终点间横纵向距离的大小来判断遍历方向
var distX:Number = Math.abs(endX - startX);
var distY:Number = Math.abs(endY - startY);
/**遍历方向,为true则为横向遍历,否则为纵向遍历*/
var loopDirection:Boolean = distX > distY ? true : false;
/**起始点与终点的连线方程*/
var lineFuction:Function;
/** 循环递增量 */
var i:Number;
/** 循环起始值 */
var loopStart:Number;
/** 循环终结值 */
var loopEnd:Number;
/** 起终点连线所经过的节点 */
var passedNodeList:Array;
var passedNode:Node;
//为了运算方便,以下运算全部假设格子尺寸为1,格子坐标就等于它们的行、列号
if( loopDirection )
{
lineFuction = MathUtil.getLineFunc(point1, point2, 0);
loopStart = Math.min( startX, endX );
loopEnd = Math.max( startX, endX );
//开始横向遍历起点与终点间的节点看是否存在障碍(不可移动点)
for( i=loopStart; i<=loopEnd; i++ )
{
//由于线段方程是根据终起点中心点连线算出的,所以对于起始点来说需要根据其中心点
//位置来算,而对于其他点则根据左上角来算
if( i==loopStart )i += .5;
//根据x得到直线上的y值
var yPos:Number = lineFuction(i);
//检查经过的节点是否有障碍物,若有则返回true
passedNodeList = getNodesUnderPoint( i, yPos );
for each( passedNode in passedNodeList )
{
if( passedNode.walkable == false )return true;
}
if( i == loopStart + .5 )i -= .5;
}
}
else
{
lineFuction = MathUtil.getLineFunc(point1, point2, 1);
loopStart = Math.min( startY, endY );
loopEnd = Math.max( startY, endY );
//开始纵向遍历起点与终点间的节点看是否存在障碍(不可移动点)
for( i=loopStart; i<=loopEnd; i++ )
{
if( i==loopStart )i += .5;
//根据y得到直线上的x值
var xPos:Number = lineFuction(i);
passedNodeList = getNodesUnderPoint( xPos, i );
for each( passedNode in passedNodeList )
{
if( passedNode.walkable == false )return true;
}
if( i == loopStart + .5 )i -= .5;
}
}
return false;
}
我的代码是在《动画高级教程》第四章“寻路”的源代码基础上改的,所以要想看懂接下来的代码,最好事先阅读过《动画高级教程》第四章的内容。
问:写hasBarrier这个方法的目的是什么?()
A:随便写着玩玩
B:for the lich king!
C:避免在不必要的时候依然使用A*寻路
D:喂,不要问不该问的东西
上题的参考答案是 C,你答对了吗?如果你答对了,那么在恭喜你的同时我们也该继续下一步操作了。通常人物的行走是由鼠标点击触发的,那么在鼠标点击事件的处理函数中,需要根据点击的目的地来选择是否启用A*寻路算法来进行寻路。
private function onGridClick(event:MouseEvent):void
{
//起点是玩家对象所在节点位置,终点是鼠标点击的节点
var startPosX:int = Math.floor(_player.x / _cellSize);
var startPosY:int = Math.floor(_player.y / _cellSize);
var endPosX:int = Math.floor(mouseX / _cellSize);
var endPosY:int = Math.floor(mouseY / _cellSize);
//判断起终点间是否存在障碍物,若存在则调用A*算法进行寻路,通过A*寻路得到的路径是一个个所要经过的节点数组;否不存在障碍则直接把路径设置为只含有一个终点元素的数组
var hasBarrier:Boolean = _grid.hasBarrier(startPosX, startPosY, endPosX, endPosY);
if( hasBarrier )
{
_grid.setStartNode(startPosX, startPosY);
_grid.setEndNode(endPosX, endPosY);
findPath();
}
else
{
_path = [_grid.getNode(endPosX, endPosY)];
_index = 0;
addEventListener(Event.ENTER_FRAME, onEnterFrame);//开始行走
}
}
private function findPath():void
{
var astar:AStar = new AStar();
if(astar.findPath(_grid))
{
_path = astar.path;
_index = 0;
addEventListener(Event.ENTER_FRAME, onEnterFrame);//开始行走
}
}
楼上的道友们欲望很强烈啊,我还没连载完就迫切地需要看看结果了,好吧,先给出一个在线预览版本让你们先把玩一下,代码也放出来先:
效果在线预览: http://we.zuisg.com/?p=257
全部源码: (附件)
让点击障碍物或者死路时可以走到离障碍物最近的点
我查了一下,网上给出的所有A*寻路算法都忽略了这点,即点击一个障碍物或死路(四周被障碍物环绕)时寻路者/玩家 就停在原地不动了,这样会让玩家有受挫、受限感,或者产生“你这个游戏有bug”的错觉。那么对于一些斜45度等角投影视角类游戏来说你玩家站原地不动是 没有多大关系的,谁叫你点了一个明显的障碍物格呢(如河流、山岭、建筑物等)

但若是对一些横版纯2D游戏来说,采用原始A*寻路这种方式就有点不能接受了……
那么要想解决这个问题,首先得找到问题的源头出在哪里,打开《动画高级教程》中提供的A*寻路源码,寻路部分代码如下:
public function search():Boolean
{
var node:Node = _startNode;
while(node != _endNode)
{
var startX:int = Math.max(0, node.x - 1);
var endX:int = Math.min(_grid.numCols - 1, node.x + 1);
var startY:int = Math.max(0, node.y - 1);
var endY:int = Math.min(_grid.numRows - 1, node.y + 1);
for(var i:int = startX; i <= endX; i++)
{
for(var j:int = startY; j <= endY; j++)
{
var test:Node = _grid.getNode(i, j);
if(test == node ||
!test.walkable ||
!_grid.getNode(node.x, test.y).walkable ||
!_grid.getNode(test.x, node.y).walkable)
{
continue;
}
var cost:Number = _straightCost;
if(!((node.x == test.x) || (node.y == test.y)))
{
cost = _diagCost;
}
var g:Number = node.g + cost * test.costMultiplier;
var h:Number = _heuristic(test);
var f:Number = g + h;
if(isOpen(test) || isClosed(test))
{
if(test.f > f)
{
test.f = f;
test.g = g;
test.h = h;
test.parent = node;
}
}
else
{
test.f = f;
test.g = g;
test.h = h;
test.parent = node;
_open.push(test);
}
}
}
for(var o:int = 0; o < _open.length; o++)
{
}
_closed.push(node);
if(_open.length == 0)
{
trace("no path found");
return false
}
_open.sortOn("f", Array.NUMERIC);
node = _open.shift() as Node;
}
buildPath();
return true;
}
了解A*算法的人都知道,所有可能被设置为路径的格子都会被放入开放列表_open中去,但是你再看16-19行这个判断:
if(test == node ||
!test.walkable ||
!_grid.getNode(node.x, test.y).walkable ||
!_grid.getNode(test.x, node.y).walkable)
{
continue;
}
这个判断会把walkable为false的点(即障碍物点)以及不可穿越点(即与上一路径点处于对角线却不可直接从对角线上通过的点,如下图)

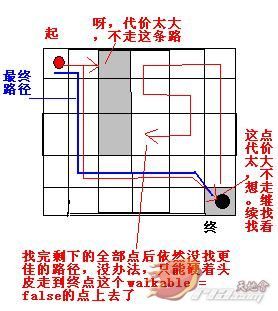
直接用 continue 语句给跳过了,这样的话不论是障碍物点还是不可穿越点都永远没有资格被加入到开启列表中去,那自然就不可能成为路径中的一员了。所以,当你点击一个障碍物 点作为终点时,你的目的是让此障碍物点成为路径中的一员,然而A*算法的上述语句却直接把障碍物点给否定掉了,那自然最终会找不出路径来了……
那么如何解决这个问题呢?首先想到的方案是寻找“替代点 ”来替代我们点击的不可移动点作为终点,但是实践证明,你永远也无法正确地找到一个“替代点”。比如,你想从你点击的那个障碍物点开始向四周遍历寻找“替代点”,如果发现了一个walkable为true的点那就把它作为“替代点”吧,这个过程如下图所示:

这种方案的结果可能是上面这种情况,找到了一个位于原目标点周围的一个替代点,这有可能是正确的一个替代点,但是如果此替代点周围又被围了一圈围墙怎么办呢?
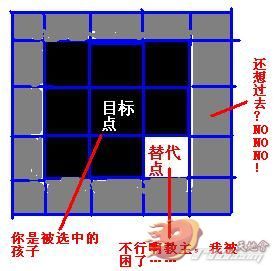
那么既然用“替代点”的方式行不通,就只能想点别的办法。在《动画高级教程》“寻路”这一章的末尾部分讲到了对一些不易行 的路径(如沼泽、高地等)增大寻路代价g值来让A*算法寻出的路径能够绕过这些不易行 的路径。
var g:Number = node.g + cost * test.costMultiplier;
上面这个costMultiplier变量是每一个节点都具备的属性,不易走的路径costMultiplier的值大,好走的路径costMultiplier值小。
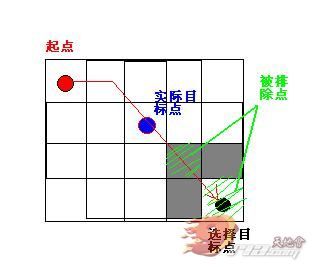
这样就给了我一个启发,既然我的目的是让我点击的障碍物点能够有机会被加到开启列表_open中,但是在路上碰到的障碍物点还是能够正常地绕开的话,不妨 把障碍物点和不可穿越点的代价costMultiplier设为一个极大的值,当A*寻路实在找不到更佳的路径时它还是会回头来找我这个障碍物点的!这个 过程如下图所示:
有人说,那按你这样子走的话,我寻路者不是要走到障碍物里头去啦?不要着急,不要着急,休息,休息一会儿……咳咳,其实我还留了一手,那就是当你寻路完毕 返回一个路径数组path后,我会从前往后对path进行遍历,一旦遇到walkable为false或是不可穿越点就把path中位于这一点之后的全部 点都TMD给我飞掉去,避免这些孽畜再为祸人间!
最后,看看代码的实现过程吧,下面给出的是经过修改的search方法以及buildPath方法:
public function search():Boolean
{
var startTime:int=getTimer();
var node:Node = _startNode;
var sortTime:int = 0;
var tryCount:int = 0;
while(node != _endNode)
{
tryCount++;
var startX:int = Math.max(0, node.x - 1);
var endX:int = Math.min(_grid.numCols - 1, node.x + 1);
var startY:int = Math.max(0, node.y - 1);
var endY:int = Math.min(_grid.numRows - 1, node.y + 1);
for(var i:int = startX; i <= endX; i++)
{
for(var j:int = startY; j <= endY; j++)
{
var test:Node = _grid.getNode(i, j);
if(test == node)
{
continue;
}
if( !test.walkable || !isDiagonalWalkable(node, test) )
{
//设其代价为超级大的一个值,比大便还大哦~
test.costMultiplier = 1000;
}
else
{
test.costMultiplier = 1;
}
var cost:Number = _straightCost;
if(!((node.x == test.x) || (node.y == test.y)))
{
cost = _diagCost;
}
var g:Number = node.g + cost * test.costMultiplier;
var h:Number = _heuristic(test);
var f:Number = g + h;
if( isOpen(test) || isClosed(test)))
{
if(test.f > f)
{
test.f = f;
test.g = g;
test.h = h;
test.parent = node;
}
}
else
{
test.f = f;
test.g = g;
test.h = h;
test.parent = node;
_open.push( test );
}
}
}
_closed.push(node);
if(_open.length == 0)
{
trace("no path found");
return false
}
var sortStartTime:int = getTimer();
_open.sortOn("f", Array.NUMERIC);
sortTime += (getTimer() - sortStartTime);
node = _open.shift() as Node;
}
trace( "time cost: " + (getTimer() - startTime) + "ms");
trace( "sort cost: " + sortTime);
trace( "try time: " + tryCount);
buildPath();
return true;
}
private function buildPath():void
{
_path = new Array();
var node:Node = _endNode;
_path.push(node);
//不包含起始节点
while(node.parent != _startNode)
{
node = node.parent;
_path.unshift(node);
}
//排除无法移动点
var len:int = _path.length;
for( var i:int=0; i<len; i++ )
{
if( _path[i].walkable == false )
{
_path.splice(i, len-i);
break;
}
//由于之前排除了起始点,所以当路径中只有一个元素时候判断该元素与起始点是否是不可穿越关系,若是,则连最后这个元素也给他弹出来~
else if( len == 1 && !isDiagonalWalkable(_startNode, _endNode) )
{
_path.shift();
}
//判断后续节点间是否存在不可穿越点,若有,则把此点之后的元素全部拿下
else if( i < len - 1 && !isDiagonalWalkable(_path[i], _path[i+1]) )
{
_path.splice(i+1, len-i-1);
break;
}
}
}
/** 判断两个节点的对角线路线是否可走 */
private function isDiagonalWalkable( node1:Node, node2:Node ):Boolean
{
var nearByNode1:Node = _grid.getNode( node1.x, node2.y );
var nearByNode2:Node = _grid.getNode( node2.x, node1.y );
if( nearByNode1.walkable && nearByNode2.walkable )return true;
return false;
}
上面的代码中我只改了几句,所以应该很容易就看出来差别在哪,我还加了几句测试语句用来测试寻路总耗时、排序耗时以及寻路过程中的试探次数以便之后进行效 率探讨。我还对buildPath方法做了更改,原始A*算法会在最终返回的path中包含起始点,其实这是没有必要的,如果你包含了起始点的话会造成下 图这种走回头路的结果:
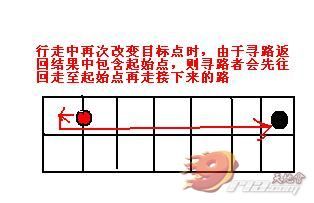
之后,对寻路返回路径进行刚才所说的处理,去掉无效路径后就能得到正确的路径了。
算法效率优化
上面代码中加了几句测试效率的语句,在debug时候可以打印出寻路总耗时、对开放列表进行排序的总耗时以及寻路总尝试次数。当你按照我刚才给出的算法 去点击一个障碍物点进行寻路的时候,虽然能够找到正确的路径,但是会发现try time的值非常大,总耗时也不低。这是因为我把障碍物点的代价设置为很大后A*寻路会先掠过此点并找寻更佳的点,它不找完剩余全部的节点是不会甘心的。 对于这种情况,网上有一些解决方案,比如将整个网格划分成几个区域等方法,这些方案我没有尝试过,因为怕会出现什么差错。那么既然不能降低尝试次数,只好 从代码执行效率上来做做功课。在《动画高级教程》中提供的AStar.as源码中存在一些会减慢效率的代码:
1.将代码中的Math.abs()方法、Math.max()、Math.min()方法用 ? : 这个三元运算符来替代;
if(isOpen(test) || isClosed(test))
使用了isOpen和isClosed两个函数来判断test点是否存在于_open和_close这两个数组中,然而我们看看isOpen和isClosed这两个函数中是怎么做的:
private function isOpen(node:Node):Boolean
{
for(var i:int = 0; i < _open.length; i++)
{
if(_open[i] == node)
{
return true;
}
}
return false;
}
作者使用这种逐个遍历的方式来查找一个元素是否在一个数组中,这种方式的效率远远比数组自带的indexOf方法低下,因此,用Array.indexOf方法来替代isOpen与isClosed方法:
if(_open.indexOf(test) != -1 || _closed.indexOf(test) != -1)
经过上面两步优化之后,调试一下,发现效率有所提高,但是我们发现排序时间依然花了不少,占总耗时的50%左右,那么我想到使用网上流行的二叉堆法来替代数组自带的sortOn方法。
什么是二叉堆法呢?先看看有关二叉堆这个数据结构的介绍:http://www.blueidea.com/tech/multimedia/2007/4665_3.asp
二叉堆这个数据结构的好处在于它始终能够保证堆顶的那个元素是所有元素中最小的,当堆内元素发生改变时就会进行一系列的运算以确保堆内结构一致(添加、删 除、修改时该做什么工作在上面给出的链接文章中都已说明),但是这“一系列的运算”的运算量远比直接使用数组自带的sortOn方法小,就比如这样子的一 个二叉堆: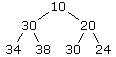
当我修改右下方的那个24为5之后,只要把24与它的父节点20交换一次位置,再与新的父节点10交换一次位置这两次操作即可,如果使用sortOn的话会遍历全部元素,消耗不少时间。当元素数量极大的时候,二叉堆的这种排序上的效率优势就更加明显了。
根据二叉堆的原理得到我们的Binary.as类:
package
{
/**
* 二叉堆数据结构
* @author S_eVent
*
*/
public class Binary
{
private var _data:Array;
private var _compareValue:String;
/**
* @param compareValue 排序字段,若为空字符串则直接比较被添加元素本身的值
*
*/
public function Binary( compareValue:String="" )
{
_data = new Array();
_compareValue = compareValue;
}
/** 向二叉堆中添加元素
* @param node 欲添加的元素对象
*/
public function push( node:Object ):void
{
//将新节点添至末尾先
_data.push( node );
var len:int = _data.length;
//若数组中只有一个元素则省略排序过程,否则对新元素执行上浮过程
if( len > 1 )
{
/** 新添入节点当前所在索引 */
var index:int = len;
/** 新节点当前父节点所在索引 */
var parentIndex:int = index / 2 - 1;
var temp:Object;
//和它的父节点(位置为当前位置除以2取整,比如第4个元素的父节点位置是2,第7个元素的父节点位置是3)比较,
//如果新元素比父节点元素小则交换这两个元素,然后再和新位置的父节点比较,直到它的父节点不再比它大,
//或者已经到达顶端,及第1的位置
while( compareTwoNodes(node, _data[parentIndex]) )
{
temp = _data[parentIndex];
_data[parentIndex] = node;
_data[index - 1] = temp;
index /= 2;
parentIndex = index / 2 - 1;
}
}
}
/** 弹出开启列表中第一个元素 */
public function shift():Object
{
//先弹出列首元素
var result:Object = _data.shift();
/** 数组长度 */
var len:int = _data.length;
//若弹出列首元素后数组空了或者其中只有一个元素了则省略排序过程,否则对列尾元素执行下沉过程
if( len > 1 )
{
/** 列尾节点 */
var lastNode:Object = _data.pop();
//将列尾元素排至首位
_data.unshift( lastNode );
/** 末尾节点当前所在索引 */
var index:int = 0;
/** 末尾节点当前第一子节点所在索引 */
var childIndex:int = (index + 1) * 2 - 1;
/** 末尾节点当前两个子节点中较小的一个的索引 */
var comparedIndex:int;
var temp:Object;
//和它的两个子节点比较,如果较小的子节点比它小就将它们交换,直到两个子节点都比它大
while( childIndex < len )
{
//只有一个子节点的情况
if( childIndex + 1 == len )
{
comparedIndex = childIndex;
}
//有两个子节点则取其中较小的那个
else
{
comparedIndex = compareTwoNodes(_data[childIndex], _data[childIndex + 1]) ? childIndex : childIndex + 1;
}
if( compareTwoNodes(_data[comparedIndex], lastNode) )
{
temp = _data[comparedIndex];
_data[comparedIndex] = lastNode;
_data[index] = temp;
index = comparedIndex;
childIndex = (index + 1) * 2 - 1;
}
else
{
break;
}
}
}
return result;
}
/** 更新某一个节点的值。在你改变了二叉堆中某一节点的值以后二叉堆不会自动进行排序,所以你需要手动
* 调用此方法进行二叉树更新 */
public function updateNode( node:Object ):void
{
var index:int = _data.indexOf( node ) + 1;
if( index == 0 )
{
throw new Error("!更新一个二叉堆中不存在的节点作甚!?");
}
else
{
var parentIndex:int = index / 2 - 1;
var temp:Object;
//上浮过程开始喽
while( compareTwoNodes(node, _data[parentIndex]) )
{
temp = _data[parentIndex];
_data[parentIndex] = node;
_data[index - 1] = temp;
index /= 2;
parentIndex = index / 2 - 1;
}
}
}
/** 查找某节点所在索引位置 */
public function indexOf( node:Object ):int
{
return _data.indexOf(node);
}
public function get length():uint
{
return _data.length;
}
/**比较两个节点,返回true则表示第一个节点小于第二个*/
private function compareTwoNodes( node1:Object, node2:Object ):Boolean
{
if( _compareValue )
{
return node1[_compareValue] < node2[_compareValue];
}
else
{
return node1 < node2;
}
return false;
}
}
}
所有二叉堆对外开放的API命名规范都效仿Array。那么有了这个类之后就开始使用它来替代原先A*算法中的Array实例吧,在A*算法中,需要排序 的只有开放列表_open这一个实例,所以只需要将_open的类型改成Binary就可以了。下面列出更改了的一些语句:
// private var _open:Array
private var _open:Binary;
……
public function findPath(grid:Grid):Boolean
{
_grid = grid;
// _open = new Array();
_open = new Binary("f");
……
return search();
}
public function search():Boolean
{
……
while(node != _endNode)
{
……
for(var i:int = startX; i <= endX; i++)
{
for(var j:int = startY; j <= endY; j++)
{
……
var g:Number = node.g + cost * test.costMultiplier;
var h:Number = _heuristic(test);
var f:Number = g + h;
var isInOpen:Boolean = _open.indexOf(test) != -1;
if( isInOpen || _closed.indexOf(test) != -1)
{
if(test.f > f)
{
test.f = f;
test.g = g;
test.h = h;
test.parent = node;
if( isInOpen )
_open.updateNode( test );
}
}
else
{
……
}
}
}
……
// _open.sortOn("f", Array.NUMERIC);
node = _open.shift() as Node;
}
buildPath();
return true;
}
最后,测试一下效率,提高了排序速率2-3倍以上……
在原A*算法的基础上做优化,我差不多就优化到这里为止,如果你的地图非常大,你想追求更进一步的快速,那看来只能换算法或者使用炼金术(alchemy)了……源码已在7楼给出~
此贴只是个人的一点思路,并引出一个话题大家讨论,相信一定有更好的方法存在.