寻找凸包的graham 扫描法
1,点集Q的凸包(convex hull)是指一个最小凸多边形,满足Q中的点或者在多边形边上或者在其内。
2,凸包最常用的凸包算法是Graham扫描法和Jarvis步进法。
3,Graham扫描法:
首先,找到所有点中最左边的(y坐标最小的),如果y坐标相同,找x坐标最小的.
以这个点为基准求所有点的极角(atan2(y-y0,x-x0)),并按照极角对这些点排序,前述基准点在最前面,设这些点为P[0]..P[n-1.
注:这样预处理后,保证p[0],p[1]和p[n-1]都是凸包上的点.
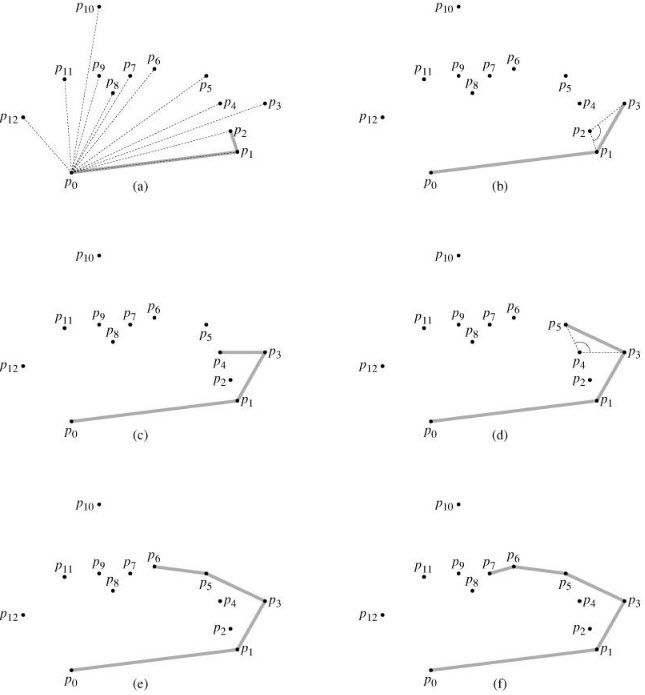
建立一个栈,初始时P[0]、P[1]、P[2]进栈,对于 P[3..n-1]的每个点,若栈顶的两个点与它不构成"向左转"的关系,则将栈顶的点出栈,直至没有点需要出栈以后将当前点进栈;
所有点处理完之后栈中保存的点就是凸包了。
图示:
4,实现代码
5,应用: http://acm.pku.edu.cn/JudgeOnline/problem?id=1113
实现代码:
2,凸包最常用的凸包算法是Graham扫描法和Jarvis步进法。
3,Graham扫描法:
首先,找到所有点中最左边的(y坐标最小的),如果y坐标相同,找x坐标最小的.
以这个点为基准求所有点的极角(atan2(y-y0,x-x0)),并按照极角对这些点排序,前述基准点在最前面,设这些点为P[0]..P[n-1.
注:这样预处理后,保证p[0],p[1]和p[n-1]都是凸包上的点.
建立一个栈,初始时P[0]、P[1]、P[2]进栈,对于 P[3..n-1]的每个点,若栈顶的两个点与它不构成"向左转"的关系,则将栈顶的点出栈,直至没有点需要出栈以后将当前点进栈;
所有点处理完之后栈中保存的点就是凸包了。
图示:

4,实现代码
#include <iostream>
#include <cmath>
using namespace std;
/*
PointSet[]:输入的点集
ch[]:输出的凸包上的点集,按照逆时针方向排列
n:PointSet中的点的数目
len:输出的凸包上的点的个数
*/
struct Point
{
float x,y;
};
//小于0,说明向量p0p1的极角大于p0p2的极角
float multiply(Point p1,Point p2,Point p0)
{
return((p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y));
}
float dis(Point p1,Point p2)
{
return(sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)));
}
void Graham_scan(Point PointSet[],Point ch[],int n,int &len)
{
int i,j,k=0,top=2;
Point tmp;
//找到最下且偏左的那个点
for(i=1;i<n;i++)
if ((PointSet[i].y<PointSet[k].y)||((PointSet[i].y==PointSet[k].y)&&(PointSet[i].x<PointSet[k].x)))
k=i;
//将这个点指定为PointSet[0]
tmp=PointSet[0];
PointSet[0]=PointSet[k];
PointSet[k]=tmp;
//按极角从小到大,距离偏短进行排序
for (i=1;i<n-1;i++)
{
k=i;
for (j=i+1;j<n;j++)
if( (multiply(PointSet[j],PointSet[k],PointSet[0])>0)
||((multiply(PointSet[j],PointSet[k],PointSet[0])==0)
&&(dis(PointSet[0],PointSet[j])<dis(PointSet[0],PointSet[k]))) )
k=j;//k保存极角最小的那个点,或者相同距离原点最近
tmp=PointSet[i];
PointSet[i]=PointSet[k];
PointSet[k]=tmp;
}
//第三个点先入栈
ch[0]=PointSet[0];
ch[1]=PointSet[1];
ch[2]=PointSet[2];
//判断与其余所有点的关系
for (i=3;i<n;i++)
{
//不满足向左转的关系,栈顶元素出栈
while(multiply(PointSet[i],ch[top],ch[top-1])>=0) top--;
//当前点与栈内所有点满足向左关系,因此入栈.
ch[++top]=PointSet[i];
}
len=top+1;
}
const int maxN=1000;
Point PointSet[maxN];
Point ch[maxN];
int n;
int len;
int main()
{
int n=5;
float x[]={0,3,4,2,1};
float y[]={0,0,0,3,1};
for(int i=0;i<n;i++)
{
PointSet[i].x=x[i];
PointSet[i].y=y[i];
}
Graham_scan(PointSet,ch,n,len);
for(int i=0;i<len;i++)
cout<<ch[i].x<<" "<<ch[i].y<<endl;
return 0;
}
5,应用: http://acm.pku.edu.cn/JudgeOnline/problem?id=1113
实现代码:
#include <iostream>
#include <cmath>
using namespace std;
/*
PointSet[]:输入的点集
ch[]:输出的凸包上的点集,按照逆时针方向排列
n:PointSet中的点的数目
len:输出的凸包上的点的个数
*/
struct Point
{
float x,y;
};
//小于0,说明向量p0p1的极角大于p0p2的极角
float multiply(Point p1,Point p2,Point p0)
{
return((p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y));
}
float dis(Point p1,Point p2)
{
return(sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)));
}
void Graham_scan(Point PointSet[],Point ch[],int n,int &len)
{
int i,j,k=0,top=2;
Point tmp;
//找到最下且偏左的那个点
for(i=1;i<n;i++)
if ((PointSet[i].y<PointSet[k].y)||((PointSet[i].y==PointSet[k].y)&&(PointSet[i].x<PointSet[k].x)))
k=i;
//将这个点指定为PointSet[0]
tmp=PointSet[0];
PointSet[0]=PointSet[k];
PointSet[k]=tmp;
//按极角从小到大,距离偏短进行排序
for (i=1;i<n-1;i++)
{
k=i;
for (j=i+1;j<n;j++)
if( (multiply(PointSet[j],PointSet[k],PointSet[0])>0)
||((multiply(PointSet[j],PointSet[k],PointSet[0])==0)
&&(dis(PointSet[0],PointSet[j])<dis(PointSet[0],PointSet[k]))) )
k=j;//k保存极角最小的那个点,或者相同距离原点最近
tmp=PointSet[i];
PointSet[i]=PointSet[k];
PointSet[k]=tmp;
}
//第三个点先入栈
ch[0]=PointSet[0];
ch[1]=PointSet[1];
ch[2]=PointSet[2];
//判断与其余所有点的关系
for (i=3;i<n;i++)
{
//不满足向左转的关系,栈顶元素出栈
while(multiply(PointSet[i],ch[top],ch[top-1])>=0) top--;
//当前点与栈内所有点满足向左关系,因此入栈.
ch[++top]=PointSet[i];
}
len=top+1;
}
const int maxN=1010;
Point PointSet[maxN];
Point ch[maxN];
int n;
int len;
int main()
{
double ans=0;
int d;
cin>>n>>d;
for(int i=0;i<n;i++)
cin>>PointSet[i].x>>PointSet[i].y;//input the data;
Graham_scan(PointSet,ch,n,len);
for(int i=0;i<len;i++)
ans+=dis(ch[i],ch[(i+1)%len]);
ans+=2*d*acos(-1.0); //等价于圆形周长
cout<<(int)(ans+0.5)<<endl; //四舍五入
return 0;
}