UVa 108 - Maximum Sum
链接:
原题:
Background
A problem that is simple to solve in one dimension is often much more difficult to solve in more than one dimension. Consider satisfying a boolean expression in conjunctive normal form in which each conjunct consists of exactly 3 disjuncts. This problem (3-SAT) is NP-complete. The problem 2-SAT is solved quite efficiently, however. In contrast, some problems belong to the same complexity class regardless of the dimensionality of the problem.
The Problem
Given a 2-dimensional array of positive and negative integers, find the sub-rectangle with the largest sum. The sum of a rectangle is the sum of all the elements in that rectangle. In this problem the sub-rectangle with the largest sum is referred to as themaximal sub-rectangle. A sub-rectangle is any contiguous sub-array of sizeor greater located within the whole array. As an example, the maximal sub-rectangle of the array:
is in the lower-left-hand corner:
and has the sum of 15.
Input and Output
The input consists of anarray of integers. The input begins with a single positive integerNon a line by itself indicating the size of the square two dimensional array. This is followed byintegers separated by white-space (newlines and spaces). Theseintegers make up the array in row-major order (i.e., all numbers on the first row, left-to-right, then all numbers on the second row, left-to-right, etc.).Nmay be as large as 100. The numbers in the array will be in the range [-127, 127].
The output is the sum of the maximal sub-rectangle.
Sample Input
4 0 -2 -7 0 9 2 -6 2 -4 1 -4 1 -1 8 0 -2
Sample Output
15
题目大意:
给一个N*N大小的矩阵,每个格子上有一个数字。 求这个矩阵中的子矩阵上面数字之和最小的数字是多少。
分析与总结:
经典的一道题。 也可以说是“最大连续和"那题(UVa 507 - Jill Rides Again)O(n)算法的升级版本。
这题的关键在于转化, 就是把矩阵上面的那些数转换成”最大连续和“。
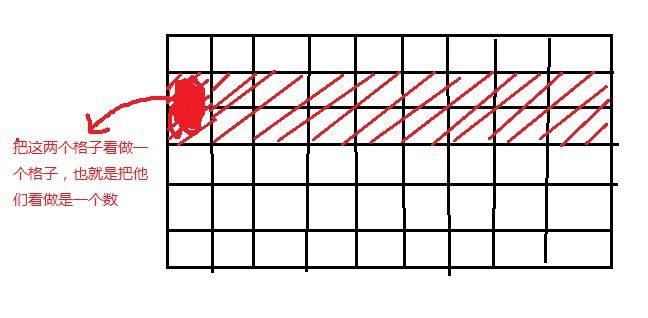
看下图(画得实在有点对不起观众 = =)
把那些格子看成数字, 上面有红色斜线阴影的代表其中一个高度为2的子矩阵, 我们可以把这两层看做是一层, 上下层数字之和代表一个新的数字, 就可以用“最大连续和”的O(n)方法求出斜线阴影部分最大的一个2*x的矩阵之和。
要求整个大矩阵的最大子矩阵数字和, 就需要枚举所层数的情况,需要用两层for循环。 加上里面那个O(n)的线性时间扫描,最终复杂度是O(n^3).
代码:
/*
* UVa: 108 - Maximum Sum
* Time: 0.012s
* Author: D_Double
*
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#define MAXN 102
using namespace std;
int arr[MAXN][MAXN],sum[MAXN][MAXN];
int mx,sm;
int main()
{
int T,m,n,x,y;
int i,j;
while(~scanf("%d",&n)){
memset(sum,0,sizeof(sum));
memset(arr,0,sizeof(arr));
for(i=1; i<=n; ++i){
for(j=1; j<=n; ++j) {
scanf("%d",&arr[i][j]);
// sum[i][j] 表示对角顶点为(1,1),(i,j)这个矩阵里面所有原数之和
sum[i][j] = sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+arr[i][j];
}
}
int maxSum=-2147483645;
for(int i=1; i<=n; ++i){
for(int j=0; j<i; ++j){
int t, min;
min=0;
for(int k=1; k<=n; ++k){ // 线性时间扫描
t=sum[i][k]-sum[j][k]-min;
if(t>maxSum) maxSum=t;
if(sum[i][k]-sum[j][k] < min)
min=sum[i][k]-sum[j][k];
}
}
}
printf("%d\n", maxSum);
}
return 0;
}
附:这题的又一次升级版UVa 10827 - Maximum sum on a torus
—— 生命的意义,在于赋予它意义。