Lucene学习总结之八:Lucene的查询语法,JavaCC及QueryParser(1)
一、Lucene的查询语法
Lucene所支持的查询语法可见http://lucene.apache.org/java/3_0_1/queryparsersyntax.html
(1) 语法关键字
+ - && || ! ( ) { } [ ] ^ " ~ * ? : \
如果所要查询的查询词中本身包含关键字,则需要用\进行转义
(2) 查询词(Term)
Lucene支持两种查询词,一种是单一查询词,如"hello",一种是词组(phrase),如"hello world"。
(3) 查询域(Field)
在查询语句中,可以指定从哪个域中寻找查询词,如果不指定,则从默认域中查找。
查询域和查询词之间用:分隔,如title:"Do it right"。
:仅对紧跟其后的查询词起作用,如果title:Do it right,则仅表示在title中查询Do,而it right要在默认域中查询。
(4) 通配符查询(Wildcard)
支持两种通配符:?表示一个字符,*表示多个字符。
通配符可以出现在查询词的中间或者末尾,如te?t,test*,te*t,但决不能出现在开始,如*test,?test。
(5) 模糊查询(Fuzzy)
模糊查询的算法是基于Levenshtein Distance,也即当两个词的差别小于某个比例的时候,就算匹配,如roam~0.8,即表示差别小于0.2,相似度大于0.8才算匹配。
(6) 临近查询(Proximity)
在词组后面跟随~10,表示词组中的多个词之间的距离之和不超过10,则满足查询。
所谓词之间的距离,即查询词组中词为满足和目标词组相同的最小移动次数。
如索引中有词组"apple boy cat"。
如果查询词为"apple boy cat"~0,则匹配。
如果查询词为"boy apple cat"~2,距离设为2方能匹配,设为1则不能匹配。
| (0) |
boy |
apple |
cat |
| (1) |
boy apple |
cat |
|
| (2) |
apple |
boy |
cat |
如果查询词为"cat boy apple"~4,距离设为4方能匹配。
| (0) |
cat |
boy |
apple |
| (1) |
cat boy |
apple |
|
| (2) |
boy |
cat apple |
|
| (3) |
boy apple |
cat |
|
| (4) |
apple |
boy |
cat |
(7) 区间查询(Range)
区间查询包含两种,一种是包含边界,用[A TO B]指定,一种是不包含边界,用{A TO B}指定。
如date:[20020101 TO 20030101],当然区间查询不仅仅用于时间,如title:{Aida TO Carmen}
(8) 增加一个查询词的权重(Boost)
可以在查询词后面加^N来设定此查询词的权重,默认是1,如果N大于1,则说明此查询词更重要,如果N小于1,则说明此查询词更不重要。
如jakarta^4 apache,"jakarta apache"^4 "Apache Lucene"
(9) 布尔操作符
布尔操作符包括连接符,如AND,OR,和修饰符,如NOT,+,-。
默认状态下,空格被认为是OR的关系,QueryParser.setDefaultOperator(Operator.AND)设置为空格为AND。
+表示一个查询语句是必须满足的(required),NOT和-表示一个查询语句是不能满足的(prohibited)。
(10) 组合
可以用括号,将查询语句进行组合,从而设定优先级。
如(jakarta OR apache) AND website
Lucene的查询语法是由QueryParser来进行解析,从而生成查询对象的。
通过编译原理我们知道,解析一个语法表达式,需要经过词法分析和语法分析的过程,也即需要词法分析器和语法分析器。
QueryParser是通过JavaCC来生成词法分析器和语法分析器的。
二、JavaCC介绍
本节例子基本出于JavaCC tutorial的文章,http://www.engr.mun.ca/~theo/JavaCC-Tutorial/
JavaCC是一个词法分析器和语法分析器的生成器。
所谓词法分析器就是将一系列字符分成一个个的Token,并标记Token的分类。
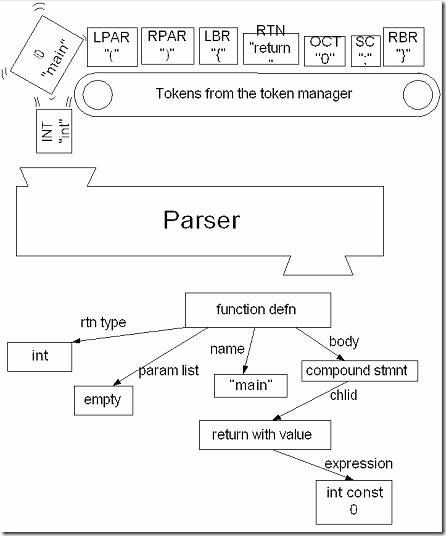
例如,对于下面的C语言程序:
| int main() { return 0 ; } |
将被分成以下的Token:
| “int”, “ ”, “main”, “(”, “)”, “”,“{”, “\n”, “\t”, “return” “”,“0”,“”,“;”,“\n”, “}”, “\n”, “” |
标记了Token的类型后如下:
| KWINT, SPACE, ID, OPAR, CPAR, SPACE, OBRACE, SPACE, SPACE, KWRETURN, SPACE, OCTALCONST, SPACE, SEMICOLON, SPACE, CBRACE, SPACE, EOF |
EOF表示文件的结束。
词法分析器工作过程如图所示:
此一系列Token将被传给语法分析器(当然并不是所有的Token都会传给语法分析器,本例中SPACE就例外),从而形成一棵语法分析树来表示程序的结构。
JavaCC本身既不是一个词法分析器,也不是一个语法分析器,而是根据指定的规则生成两者的生成器。
2.1、第一个实例——正整数相加
下面我们来看第一个例子,即能够解析正整数相加的表达式,例如99+42+0+15。
(1) 生成一个adder.jj文件
此文件中写入的即生成词法分析器和语法分析器的规则。
(2) 设定选项,并声明类
|
/* adder.jj Adding up numbers */ options { STATIC = false ; } PARSER_BEGIN(Adder) class Adder { static void main( String[] args ) throws ParseException, TokenMgrError { Adder parser = new Adder( System.in ) ; parser.Start() ; } } PARSER_END(Adder) |
STATIC选项默认是true,设为false,使得生成的函数不是static的。
PARSER_BEGIN和PARSER_END之间的java代码部分,此部分不需要通过JavaCC根据规则生成java代码,而是直接拷贝到生成的java代码中的。
(3) 声明一个词法分析器
| SKIP : { " " } SKIP : { "\n" | "\r" | "\r\n" } TOKEN : { < PLUS : "+" > } TOKEN : { < NUMBER : (["0"-"9"])+ > } |
第一二行表示空格和回车换行是不会传给语法分析器的。
第三行声明了一个Token,名称为PLUS,符号为“+”。
第四行声明了一个Token,名称为NUMBER,符号位一个或多个0-9的数的组合。
如果词法分析器分析的表达式如下:
- “123 + 456\n”,则分析为NUMBER, PLUS, NUMBER, EOF
- “123 - 456\n”,则报TokenMgrError,因为“-”不是一个有效的Token.
- “123 ++ 456\n”,则分析为NUMBER, PLUS, PLUS, NUMBER, EOF,词法分析正确,后面的语法分析将会错误。
(4) 声明一个语法分析器
| void Start() : {} { <NUMBER> ( <PLUS> <NUMBER> )* <EOF> } |
语法分析器使用BNF表达式。
上述声明将生成start函数,称为Adder类的一个成员函数
语法分析器要求输入的语句必须以NUMBER开始,以EOF结尾,中间是零到多个PLUS和NUMBER的组合。
(5) 用javacc编译adder.jj来生成语法分析器和词法分析器
最后生成的adder.jj如下:
| options PARSER_BEGIN(Adder) public class Adder SKIP : TOKEN : /* OPERATORS */ TOKEN : void start() : |
用JavaCC编译adder.jj生成如下文件:
- Adder.java:语法分析器。其中的main函数是完全从adder.jj中拷贝的,而start函数是被javacc由adder.jj描述的规则生成的。
- AdderConstants.java:一些常量,如PLUS, NUMBER, EOF等。
- AdderTokenManager.java:词法分析器。
- ParseException.java:用于在语法分析错误的时候抛出。
- SimpleCharStream.java:用于将一系列字符串传入词法分析器。
- Token.java:代表词法分析后的一个个Token。Token对象有一个整型域kind,来表示此Token的类型(PLUS, NUMBER, EOF),有一个String类型的域image,来表示此Token的值。
- TokenMgrError.java:用于在词法分析错误的时候抛出。
下面我们对adder.jj生成的start函数进行分析:
| final public void start() throws ParseException { //从词法分析器取得下一个Token,而且要求必须是NUMBER类型,否则抛出异常。 //此步要求表达式第一个出现的字符必须是NUMBER。 jj_consume_token(NUMBER); label_1: while (true) { //jj_ntk()是取得下一个Token的类型,如果是PLUS,则继续进行,如果是EOF则退出循环。 switch ((jj_ntk==-1)?jj_ntk():jj_ntk) { case PLUS: ; break; default: jj_la1[0] = jj_gen; break label_1; } //要求下一个PLUS字符,再下一个是一个NUMBER,如此下去。 jj_consume_token(PLUS); jj_consume_token(NUMBER); } } |
(6) 运行Adder.java
如果输入“123+456”则不报任何错误。
如果输入“123++456”则报如下异常:
| Exception in thread "main" org.apache.javacc.ParseException: Encountered " "+" "+ "" at line 1, column 5. |
如果输入“123-456”则报如下异常:
| Exception in thread "main" org.apache.javacc.TokenMgrError: Lexical error at line 1, column 4. Encountered: "-" (45), after : "" |
2.2、扩展语法分析器
在上面的例子中的start函数中,我们仅仅通过语法分析器来判断输入的语句是否正确。
我们可以扩展BNF表达式,加入Java代码,使得经过语法分析后,得到我们想要的结果或者对象。
我们将start函数改写为:
| int start() throws NumberFormatException : { //start函数中有三个变量 Token t ; int i ; int value ; } { //首先要求表达式的第一个一定是一个NUMBER,并把其值付给t t= <NUMBER> //将t的值取出来,解析为整型,放入变量i中 { i = Integer.parseInt( t.image ) ; } //最后的结果value设为i { value = i ; } //紧接着应该是零个或者多个PLUS和NUMBER的组合 ( <PLUS> //每出现一个NUMBER,都将其付给t,并将t的值解析为整型,付给i t= <NUMBER> { i = Integer.parseInt( t.image ) ; } //将i加到value上 { value += i ; } )* //最后的value就是表达式的和 { return value ; } } |
生成的start函数如下:
| final public int start() throws ParseException, NumberFormatException { Token t; int i; int value; t = jj_consume_token(NUMBER); i = Integer.parseInt(t.image); value = i; label_1: while (true) { switch ((jj_ntk == -1) ? jj_ntk() : jj_ntk) { case PLUS: ; break; default: jj_la1[0] = jj_gen; break label_1; } jj_consume_token(PLUS); t = jj_consume_token(NUMBER); i = Integer.parseInt(t.image); value += i; } { if (true) return value; } throw new Error("Missing return statement in function"); } |
从上面的例子,我们发现,把一个NUMBER取出,并解析为整型这一步是可以共用的,所以可以抽象为一个函数:
| int start() throws NumberFormatException : { int i; int value ; } { value = getNextNumberValue() ( <PLUS> i = getNextNumberValue() { value += i ; } )* { return value ; } } int getNextNumberValue() throws NumberFormatException : { Token t ; } { t=<NUMBER> { return Integer.parseInt( t.image ) ; } } |
生成的函数如下:
|
final public int start() throws ParseException, NumberFormatException { int i; int value; value = getNextNumberValue(); label_1: while (true) { switch ((jj_ntk == -1) ? jj_ntk() : jj_ntk) { case PLUS: ; break; default: jj_la1[0] = jj_gen; break label_1; } jj_consume_token(PLUS); i = getNextNumberValue(); value += i; } { if (true) return value; } throw new Error("Missing return statement in function"); } final public int getNextNumberValue() throws ParseException, NumberFormatException { Token t; t = jj_consume_token(NUMBER); { if (true) return Integer.parseInt(t.image); } throw new Error("Missing return statement in function"); } |
2.3、第二个实例:计算器
(1) 生成一个calculator.jj文件
用于写入生成计算器词法分析器和语法分析器的规则。
(2) 设定选项,并声明类
| options { STATIC = false ; } PARSER_BEGIN(Calculator) import java.io.PrintStream ; class Calculator { static void main( String[] args ) throws ParseException, TokenMgrError, NumberFormatException { Calculator parser = new Calculator( System.in ) ; parser.Start( System.out ) ; } double previousValue = 0.0 ; } PARSER_END(Calculator) |
previousValue用来记录上一次计算的结果。
(3) 声明一个词法分析器
| SKIP : { " " } TOKEN : { < EOL:"\n" | "\r" | "\r\n" > } TOKEN : { < PLUS : "+" > } |
我们想要支持小数,则有四种情况:没有小数,小数点在中间,小数点在前面,小数点在后面。则语法规则如下:
| TOKEN { < NUMBER : (["0"-"9"])+ | (["0"-"9"])+ "." (["0"-"9"])+ | (["0"-"9"])+ "." | "." (["0"-"9"])+ > } |
由于同一个表达式["0"-"9"]使用了多次,因而我们可以定义变量,如下:
| TOKEN : { < NUMBER : <DIGITS> | <DIGITS> "." <DIGITS> | <DIGITS> "." | "." <DIGITS>> } TOKEN : { < #DIGITS : (["0"-"9"])+ > } |
(4) 声明一个语法分析器
我们想做的计算器包含多行,每行都是一个四则运算表达式,语法规则如下:
| Start -> (Expression EOL)* EOF |
| void Start(PrintStream printStream) throws NumberFormatException : {} { ( previousValue = Expression() <EOL> { printStream.println( previousValue ) ; } )* <EOF> } |
每一行的四则运算表达式如果只包含加法,则语法规则如下:
| Expression -> Primary (PLUS Primary)* |
| double Expression() throws NumberFormatException : { double i ; double value ; } { value = Primary() ( <PLUS> i= Primary() { value += i ; } )* { return value ; } } |
其中Primary()得到一个数的值:
| double Primary() throws NumberFormatException : { Token t ; } { t= <NUMBER> { return Double.parseDouble( t.image ) ; } } |
(5) 扩展词法分析器和语法分析器
如果我们想支持减法,则需要在词法分析器中添加:
| TOKEN : { < MINUS : "-" > } |
语法分析器应该变为:
| Expression -> Primary (PLUS Primary | MINUS Primary)* |
| double Expression() throws NumberFormatException : { double i ; double value ; } { value = Primary() ( <PLUS> i = Primary() { value += i ; } | <MINUS> i = Primary() { value -= i ; } )* { return value ; } } |
如果我们想添加乘法和除法,则在词法分析器中应该加入:
| TOKEN : { < TIMES : "*" > } TOKEN : { < DIVIDE : "/" > } |
对于加减乘除混合运算,则应该考虑优先级,乘除的优先级高于加减,应该先做乘除,再做加减:
| Expression -> Term (PLUSTerm | MINUSTerm)* Term -> Primary (TIMES Primary | DIVIDE Primary)* |
| double Expression() throws NumberFormatException : { double i ; double value ; } { value = Term() ( <PLUS> i= Term() { value += i ; } | <MINUS> i= Term() { value -= i ; } )* { return value ; } } |
| double Term() throws NumberFormatException : { double i ; double value ; } { value = Primary() ( <TIMES> i = Primary() { value *= i ; } | <DIVIDE> i = Primary() { value /= i ; } )* { return value ; } } |
下面我们要开始支持括号,负号,以及取得上一行四则运算表达式的值。
对于词法分析器,我们添加如下Token:
| TOKEN : { < OPEN PAR : "(" > } TOKEN : { < CLOSE PAR : ")" > } TOKEN : { < PREVIOUS : "$" > } |
对于语法分析器,对于最基本的表达式,有四种情况:
其可以是一个NUMBER,也可以是上一行四则运算表达式的值PREVIOUS,也可以是被括号括起来的一个子语法表达式,也可以是取负的一个基本语法表达式。
| Primary –> NUMBER | PREVIOUS | OPEN_PAR Expression CLOSE_PAR | MINUS Primary |
| double Primary() throws NumberFormatException : { Token t ; double d ; } { t=<NUMBER> { return Double.parseDouble( t.image ) ; } | <PREVIOUS> { return previousValue ; } | <OPEN PAR> d=Expression() <CLOSE PAR> { return d ; } | <MINUS> d=Primary() { return -d ; } } |
(6) 用javacc编译calculator.jj来生成语法分析器和词法分析器
最后生成的calculator.jj如下:
| options PARSER_BEGIN(Calculator) SKIP : { " " } void start(PrintStream printStream) throws NumberFormatException : double Expression() throws NumberFormatException : double Term() throws NumberFormatException : double Primary() throws NumberFormatException : |
生成的start函数如下:
| final public void start(PrintStream printStream) throws ParseException, NumberFormatException { label_1: while (true) { switch ((jj_ntk==-1)?jj_ntk():jj_ntk) { case MINUS: case NUMBER: case OPEN_PAR: case PREVIOUS: ; break; default: jj_la1[0] = jj_gen; break label_1; } previousValue = Expression(); printStream.println( previousValue ) ; } } final public double Expression() throws ParseException, NumberFormatException { double i ; double value ; value = Term(); label_2: while (true) { switch ((jj_ntk==-1)?jj_ntk():jj_ntk) { case PLUS: case MINUS: ; break; default: jj_la1[1] = jj_gen; break label_2; } switch ((jj_ntk==-1)?jj_ntk():jj_ntk) { case PLUS: jj_consume_token(PLUS); i = Term(); value += i ; break; case MINUS: jj_consume_token(MINUS); i = Term(); value -= i ; break; default: jj_la1[2] = jj_gen; jj_consume_token(-1); throw new ParseException(); } } {if (true) return value ;} throw new Error("Missing return statement in function"); } final public double Term() throws ParseException, NumberFormatException { double i ; double value ; value = Primary(); label_3: while (true) { switch ((jj_ntk==-1)?jj_ntk():jj_ntk) { case TIMES: case DIVIDE: ; break; default: jj_la1[3] = jj_gen; break label_3; } switch ((jj_ntk==-1)?jj_ntk():jj_ntk) { case TIMES: jj_consume_token(TIMES); i = Primary(); value *= i ; break; case DIVIDE: jj_consume_token(DIVIDE); i = Primary(); value /= i ; break; default: jj_la1[4] = jj_gen; jj_consume_token(-1); throw new ParseException(); } } {if (true) return value ;} throw new Error("Missing return statement in function"); } final public double Primary() throws ParseException, NumberFormatException { Token t ; double d ; switch ((jj_ntk==-1)?jj_ntk():jj_ntk) { case NUMBER: t = jj_consume_token(NUMBER); {if (true) return Double.parseDouble( t.image ) ;} break; case PREVIOUS: jj_consume_token(PREVIOUS); {if (true) return previousValue ;} break; case OPEN_PAR: jj_consume_token(OPEN_PAR); d = Expression(); jj_consume_token(CLOSE_PAR); {if (true) return d ;} break; case MINUS: jj_consume_token(MINUS); d = Primary(); {if (true) return -d ;} break; default: jj_la1[5] = jj_gen; jj_consume_token(-1); throw new ParseException(); } throw new Error("Missing return statement in function"); } |