SummedAreaTable

1984年的始祖文章：

http://www.soe.ucsc.edu/classes/cmps160/Fall05/papers/p207-crow.pdf

 

后来的一些：

http://www.shaderwrangler.com/publications/sat/SAT_EG2005.pdf （这个比较好）

http://ati.amd.com/developer/gdc/GDC2005_SATEnvironmentReflections.pdf

 

summed area table对应的技术最接近的是mipmap，mipmap每一阶的标准做法是上一阶对应的4个像素的平均（某些情况是2个）。

也就是说在mipmap的情况下我们要拿一些平均过的texel就被局限到这种正方形（某些情况是长方形）的kernal里，如果想有更多种类的取法，1*3,2*5这种，那么会直接导致性能变化剧烈。

summed area table则提供了可以在恒定时间（如果不考虑texture sample cache效率，认为texture sample都是一样时间的话）在一定范围内任意矩形的sample kernel。

 

实际应用中，真正比mipmap强力的地方大抵是这些，在summed area table variance shadow map里有个比较好的实例应用：

http://http.developer.nvidia.com/GPUGems3/gpugems3_ch08.html

尤其是里面percentage closer shadow map那个应用。

 

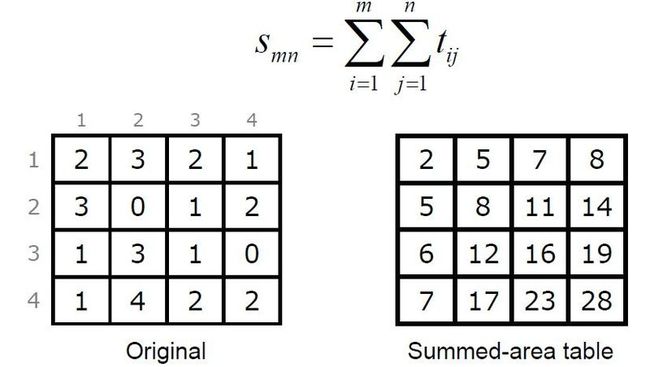
先上算法，给定一个texture，需要先构建这个summed area table:

 

里面每个element是它左边和上面所有texel的值的和。

图示：

 

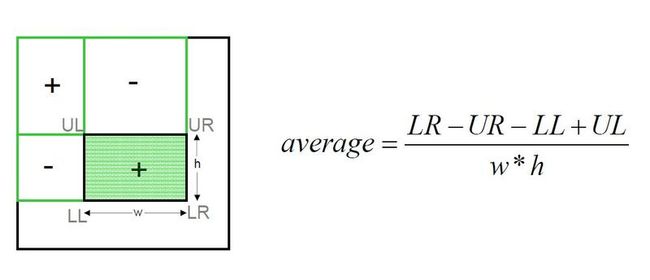
filter summed area table,在使用SAT的时候，根据要sample的kernel，结果的定义：

 

 

 

 

filter这一步可以看到，只要取4个pixel就可以实现对任意矩形形状内部的texel的平均值计算，这也是SAT强力的地方。

代码：

float4tex2D_SAT_blur(samplertSAT, float2uv, float2size)
{
     float4result = tex2D(tSAT, uv+ 0.5 * size); // LR
     result -= tex2D(tSAT, uv+ float2(0.5, -0.5) * size); // UR
     result -= tex2D(tSAT, uv+ float2(-0.5, 0.5) * size); // LL
     result += tex2D(tSAT, uv-0.5 * size); // UL
     result /= size.x* size.y;
     return result;
}

 

具体应用的时候效率和精度是考虑重点，构建SAT过程中有用到一个recurcive doubling的方法来快速构建。

 

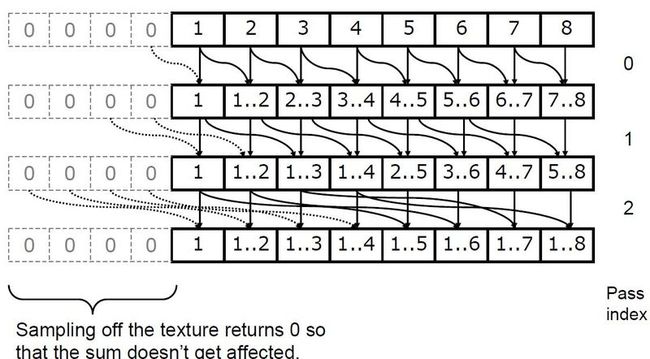
 recursive doubling就是一种非常适合多线程并行计算的东西，单线程的pipeline指令也可以从中受益很多，图示：

 

 

这样log_2（n）次可以搞定。

实际应用中，每个pass可以sample更多的texel，而且可以再log_sample_num(n)pass构建好。

 

另一个是精度问题，因为存的东西可能值非常大，所以需要24bit或者32bit精度的texture来保存，这个有点寒。。。

另外偏移0.5在sample初始texture和构建SAT过程中也会增加一些精度。

 

 

所以总体下来，不太好说这个技术好用不好用。

虽然在adaptive kernel上有好的表现，但是更多的pass和精度要求又带来performance和空间上的消耗。

另外比如说要把shadow map升级到pcss这种，这个就要有额外的开销，这个只有要实现出来profile了才能做最后的决定。

 

但是的确是一个很有意思的技术。

 

 

原文链接： http://blog.csdn.net/ccanan/article/details/5117900