The high-level organization of Pregel programs is inspired by Valiant’s Bulk Synchronous Parallel model . Pregel
computations consist of a sequence of iterations, called supersteps. During a superstep the framework invokes a user-defined function for each vertex, conceptually in parallel.The function specifies behavior at a single vertex V and a single superstep S. It can read messages sent to V in superstep S − 1, send messages to other vertices that will be received at superstep S + 1, and modify the state of V and its outgoing edges. Messages are typically sent along outgoing edges, but a message may be sent to any vertex whose identifier is known.
The input to a Pregel computation is a directed graph in which each vertex is uniquely identified by a string vertex
identifier. Each vertex is associated with a modifiable, user defined value. The directed edges are associated with their source vertices, and each edge consists of a modifiable, user defined value and a target vertex identifier.
A typical Pregel computation consists of input, when the graph is initialized, followed by a sequence of supersteps separated by global synchronization points until the algorithm terminates, and finishing with output.
Within each superstep the vertices compute in parallel,each executing the same user-defined function that expresses the logic of a given algorithm. A vertex can modify its state or that of its outgoing edges, receive messages sent to it in the previous superstep, send messages to other vertices (to be received in the next superstep), or even mutate the topology of the graph. Edges are not first-class citizens in this model, having no associated computation.
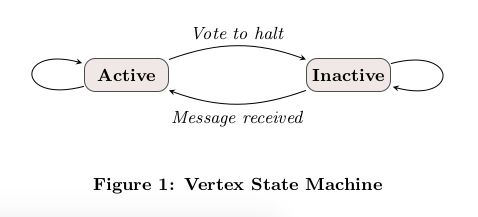
Algorithm termination is based on every vertex voting to halt. In superstep 0, every vertex is in the active state; all active vertices participate in the computation of any given superstep. A vertex deactivates itself by voting to halt. This means that the vertex has no further work to do unless triggered externally, and the Pregel framework will not execute that vertex in subsequent supersteps unless it receives a message. If reactivated by a message, a vertex must explicitly deactivate itself again. The algorithm as a whole terminates when all vertices are simultaneously inactive and there are no messages in transit. This simple state machine is illustrated in Figure 1.
The output of a Pregel program is the set of values explicitly output by the vertices. It is often a directed graph
isomorphic to the input, but this is not a necessary property of the system because vertices and edges can be added and removed during computation. A clustering algorithm,for example, might generate a small set of disconnected vertices selected from a large graph. A graph mining algorithm might simply output aggregated statistics mined from the graph.
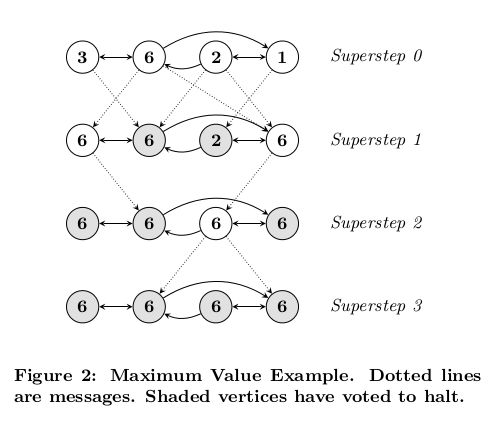
Figure 2 illustrates these concepts using a simple example:given a strongly connected graph where each vertex contains a value, it propagates the largest value to every vertex. In each superstep, any vertex that has learned a larger value from its messages sends it to all its neighbors. When no further vertices change in a superstep, the algorithm terminates.
We chose a pure message passing model, omitting remote reads and other ways of emulating shared memory, for two reasons. First, message passing is sufficiently expressive that there is no need for remote reads. We have not found any graph algorithms for which message passing is insufficient.Second, this choice is better for performance. In a cluster environment, reading a value from a remote machine incurs high latency that can’t easily be hidden. Our message passing model allows us to amortize latency by delivering messages asynchronously in batches.
Graph algorithms can be written as a series of chained MapReduce invocations [11, 30]. We chose a different model for reasons of usability and performance. Pregel keeps vertices and edges on the machine that performs computation,and uses network transfers only for messages. MapReduce,however, is essentially functional, so expressing a graph algorithm as a chained MapReduce requires passing the entire state of the graph from one stage to the next—in general requiring much more communication and associated serialization overhead. In addition, the need to coordinate the steps of a chained MapReduce adds programming complexity that is avoided by Pregel’s iteration over supersteps.
The orignal paper see:
Grzegorz Malewicz, Matthew H. Austern, 《Pregel: A System for Large-Scale Graph Processing》