uva 1382 - Distant Galaxy
题意:给出平面上的n个点,找出一个矩形,使得边界上含有尽量多的点
思路:
1 很清楚,如果输入的n个点在同一行或者同一列的话那么ans = n。还有一种情况就是n个点的横坐标和纵坐标只有2种,那么这种情况ans = n。
2 对于这一题我们考虑的是枚举矩形的上下边界(纵坐标),然后利用其它的方法求左右边界,见下图
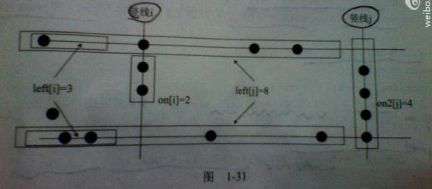
3 对于竖线i,我们用left[i]表示竖线左边位于上下边界的点数(不包括位于竖线i), on[i]表示竖线上位于上下边界之间的点数(和on2[i]的区别就是on[i]不统计位于上下边界的点数),这样给定左右边界i和j的话,矩形边界上的点数为left[j]+on2[j]+on[i]-left[i],当有边界j确定的时候,on[i]-left[i]要最大
4 那么我们枚举完上下边界后,我们利用O(n)的时间去求left[] , on[] , on2[],然后枚举有边界j,维护最大的on[i]-left[i]
代码:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 110;
struct Node{
int x;
int y;
bool operator<(const Node& s)const{
return x < s.x;
}
};
Node node[MAXN];
int n , numy[MAXN];
int solve(){
sort(node , node+n);
sort(numy , numy+n);
int num = unique(numy , numy+n)-numy;
if(num <= 2)//如果纵坐标最多只有2个那么ans = n
return n;
//枚举上下界
int miny , maxy , ans;
int left[MAXN] , on[MAXN] , on2[MAXN];
ans = 0;
for(int i = 0 ; i < num ; i++){
for(int j = i+1 ; j < num ; j++){
miny = numy[i];
maxy = numy[j];
//求left , on , on2数组;
int k = -1;
memset(left , 0 , sizeof(left));
memset(on , 0 , sizeof(on));
memset(on2 , 0 , sizeof(on2));
for(int t = 0 ; t < n ; t++){
if(!t || node[t].x != node[t-1].x){
k++;
left[k] = k == 0 ? 0 : left[k-1]+on2[k-1]-on[k-1];
}
if(node[t].y > miny && node[t].y < maxy)
on[k]++;
if(node[t].y >= miny && node[t].y <= maxy)
on2[k]++;
}
if(k <= 1)//如果横坐标最多只有2个那么ans = n
return n;
int Max = 0;
for(int t = 0 ; t <= k ; t++){
ans = max(ans , left[t]+on2[t]+Max);
Max = max(Max , on[t]-left[t]);
}
}
}
return ans;
}
int main(){
int Case = 1;
while(scanf("%d" , &n) && n){
for(int i = 0 ; i < n ; i++){
scanf("%d%d" , &node[i].x , &node[i].y);
numy[i] = node[i].y;
}
printf("Case %d: %d\n" , Case++ , solve());
}
return 0;
}