8任务独立规则
![]()
《树型软件工程方法》之系列博文8
任务独立规则
TREESOFT
目 录
8 任务独立规则. 1
8.1 任务独立的基本原理.... 1
8.2 任务独立规则.... 2
8.2.1 相关专用名词.... 2
8.2.2 作业树中的同宗延续.... 3
8.2.3 含有控制的Dq独立规则.... 3
8.2.4 不含控制的Dq独立规则.... 5
8.3 任务范畴的限定.... 7
8.4 结束语.... 7
中国人为什么不可以有自己的软件工程方法及其开发工具平台!
这是介绍《树型软件工程方法》的系列博文,请按文章标题所带的编号顺序阅读,否则你会看不懂本文。
8 任务独立规则
在博文《解一元高方程的任务树》中我们定义作业树所形成的程序段为任务,实际上并没有限定任务的作用范畴,因为作业树的范畴并没有被限定。任务确定作业树,作业树又定义任务,他们互为定义显然是不行的。按“概念”独立出任务到是可行的,只不过概念本身也没有定义,只可意会,无法言传。由此可见,形成任务树的关键还在于如何划分任务,或者说依据什么来限定任务的范畴。本文将要深入地讨论这方面的问题。我们将会看到,任务的作用范畴是严格的,任务的独立是有严密的数学依据的。
8.1 任务独立的基本原理
实际上,人们长期以来都是按概念来独立任务,即按概念来确定“子程序”或“C函数”。由此可见:
按概念形成任务是任务独立的基本原理。
解一元高次方程的问题中有四个独立概念,他们分别是:
1) 选取x1和x2的初值。
输入x1和x2,使之满足f(x1)*f(x2)<0,以保证曲线上两点(x1,f(x1))和(x2,f(x2))的连线与X轴相交。按此概念形成了图7.2中的C函数init()的作业树。
2) 求弦截线与x轴的交点。
曲线上两点(x1,f(x1))和(x2,f(x2))的连线与X轴的交点为(x,0),其中x按下式求解:
x=(x1*f(x2)-x2*f(x1))/(f(x2)-f(x1)) (f(x1)*f(x2)<0)
按此概念形成了图7.3中的C函数xpoint()的作业树。
3) 求曲线上的点。
(x,y)是曲线y=f(x)=x3-5x2+16x-80上的一点。将给定的x代入该方程,就可求得相应的y。按此概念形成了图7.4中的C函数f(x)的作业树。
4) 迭代求方程的根。
弦截法是逐步逼近y=0的,每次都是在上一次的基础上,按弦与X轴的交点更换曲线上的点以便得到新的弦,求出新的y。为此,在保证f(x1)*f(x2)<0的前提下,每次都要确定新的x1或x2。当迭代过程中出现y<ε时,说明y近似等于0,则认为此时的x值即为方程的解。按此概念形成了图7.5中的C函数main()的作业树。
上述独立出任务的核心理念是“明晰概念”,即应该将具有常规概念的问题独立形成任务。所谓“常规概念”,即人们通常认可的概括某独立范畴的概念。认为按概念形成任务是任务独立的基本原理,既可直接用于按常理去独立任务,也包括了接下来将要叙述的按规则独立任务的方法。
8.2 任务独立规则
上面叙述了任务独立的基本原理。本节将会依据这个原理,从数学的角度归纳出严格可行的任务独立规则。我们将会看到,虽然任务独立的情况相当复杂,但还是有章可循的,甚至可以由计算机辅助系统自动找出应该独立的任务。
8.2.1 相关专用名词
本节将要定义相关专用名词,以方便后面的叙述。前三个在博文《作业树设计原理》中己有过定义,后三个则是本文定义的。
(1) 原问题
作业树所求解的问题称为原问题,简记为Oq。如博文《解一元高次方程的任务树》中的每一棵作业树都对应于一个Oq。显然,一个Oq就对应于一个任务。
(2) 源问题
作业子树所求解的问题称为源问题,简记为Sq。如博文《解一元高次方程的任务树》中任意一棵作业树的任意一个节点为根的作业子树,都求解一个相应的Sq。Oq包含所有的Sq,是作业树中最大的Sq。
(3) 真问题
作业节点及其左子树所组成的作业子树所求解的问题称为真问题,简记为Tq。每个Sq至少含有一个Tq,剪去Sq根节点的右子树和中子树后剩下的作业子树就是与该Sq同根的Tq。
(4) 解后段
作业树中控制节点的中口所连接的非问题求解性的作业子树称为解后段,简记为Rs(Remainder segment after having solved),该控制节点称为Rs的父亲。Rs只对以其父亲为根的Sq所求解的结果做存储、传送、输出等非加工性的操作,不能含有改变该结果值或将该结果用于计算等问题求解性的操作。如博文《解一元高次方程的任务树》中图7.5中任务Rt的作业树中节点C1的中口所连接的程序段“print x”就一个Rs。
(5) 异宗问题
如果原问题 Oq1的作业树中存在的另一个原问题 Oq2的求解子树,称Oq2为Oq1作业树中的异宗问题,简记为Dq(Different question)。也称Oq2是Oq1的异宗插入。博文《解一元高次方程的任务树》中没有Dq,因为他们都是规范的作业树。如果作业树中存在Dq,就应该将其独立成任务。
Dq必定是Tq。由于Dq是另一个Oq的求解子树,其就必定有初始型态树,亦即有Tq型态树。换句话说,Dq是以Tq的形式接入于某作业树的,所以Dq必定是Tq。
(6) 中口问题
作业树中控制节点的中口所连接的Sq称为中口问题,简记为Mq(Middle question),相应控制节点称为Mq的父亲。博文《解一元高次方程的任务树》中没有Mq,因为它的出现将意味着有Dq的存在,这在后面会有详述。Mq和Rs虽然都连接于控制作业的中口,但它们是不同的两个概念,Mq是要求解问题的,Rs则不求解问题。后面将会说明,控制节点的中口如果连接有子树,或者是Mq,或者是Rs,不存在他们接于同一个中口的现象。
注意,Mq和Rs都是Sq,它们的根节点不是连接它们的那个控制节点,而是这个控制节点中口所连接的节点。
8.2.2 作业树中的同宗延续
上一节定义了异宗问题,显然是相对于同宗而言的。换句话说,作业树中的节点之间的关系应该是同宗的。本节将要讨论这种同宗关系,以便在作业树中发现Dq。
由作业树的设计原理可知:控制节点左口连接的是Tq的求解子树,右口可以连接Sq的另一个Tq。问题的求解只能由Tq承担,完成所有Tq的求解就完成了Oq的求解。又由作业树的运行机理可知:运行过Tq的左子树是Tq“求解已结束”为“真”的充要条件。而Tq的求解是自顶向下连续嵌套推进的,只有当最后一级Tq(作业树的叶节点)求解结束后,才会自底向上连续有Tq的求解结束。
作业树中依Oq的求解逻辑连续嵌套地形成Tq的现象称为同宗延续。
上述断语即为“同宗延续”的定义。这个定义实际是指出了作业树中父子节点之间的同宗(延续)关系。作业树中每一个节点都对应于一个Tq,都必须满足作业树的运行机理,亦即都必须由同宗延续生成。由作业树的初始型态树可知,作业树的根节点是祖宗,其它所有节点都是源自这个祖宗逐级延续生成的。
8.2.3 含有控制的Dq独立规则
我们已经弄清楚了父子作业节点之间是同宗关系。现在来考察作业树中存在有Dq的情况。本节先考察含有控制的Dq,稍后再讨论不含控制的Dq。为了叙述的方便,如果控制节点C是Sq的根,则简记为C-Sq。类似地还有C-Tq,C-Dq。如果控制节点C是Mq或Rs的父亲,则简记为C-Mq或C-Rs。
任务独立规则1:作业树中某Tq是Dq的充要条件是该Tq根节点的中口接有Mq。
这个结论看上去像是判断准则,实际也的确是判断作业树中是否存在Dq的判断准则。当然他也是任务独立的规则,既然已经判断出Dq的存在,就应该将其独立成任务。由于是充要条件,就需要从正向和逆向两方面去证明这个结论。下面证明中作业树的控制类型只用了“?”并不失一般性,可以是任意的控制类型。
先从正向证明任务独立规则1:如果某Tq是Dq,则该Tq根节点的中口必定接有Mq。
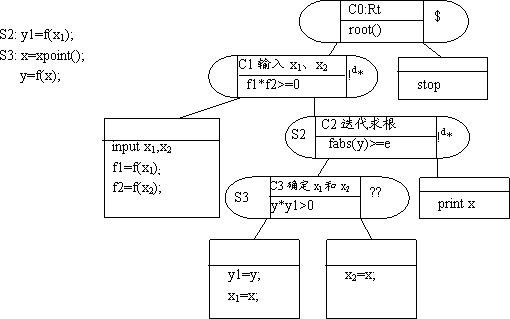
如图8.1所示,设该图中的C2-Tq是Dq。由Dq定义可知,C2不是C1的同宗延续。既然C2是异宗插入,则C2-Tq的求解结束并不能导致C1-Tq的求解结束,C1-Tq的求解还另有通路。而C3属于C1-Tq中仅有的另一个可延伸的控制节点,除C2的叶节点外,C3是C1-Tq求解过程中可以抵达叶节点的必经节点。这说明,C3是C1的后代,他们是同宗的,C1-Tq的求解结束依赖于C3-Sq的求解结束。又因为C2-Tq是Dq,C3和C2不是同宗的,C3就不可能接于C2的左口或右口。为了延续C1-Tq的求解,C3只能接于C2的中口,即C2的中口所接的子树C3-Sq必定是Mq。C2-Dq的异宗插入间断了C1和C3之间的同宗延续,C2-Dq是为C3-Sq准备数据的,以便完成C1-Tq的求解。这就从正向证明了任务独立规则1的成立。
图8.1 含有异宗插入的作业树
再从逆向证明:如果某控制节点的中口接有Mq,则以该控制节点为根的Tq就是Dq。
我们仍以图8.1的作业树为讨论对象,设C3-Sq是Mq。首先,由于C3接于C2的中口,说明C2-Sq先运行,然后才会运行C3-Sq。C2-Sq的求解结束并不需要等待C3-Sq的求解结束,C3并不是C2的同宗延续。其次,由于C2-Sq是C1-Tq的问题求解子树,C2-Sq的求解结束就意味着C1-Tq的求解结束。又因为C3-Sq是Mq,尽管C2-Sq的求解己经结束,可C1-Tq的求解却仍未结束,说明C2并不是C1的同宗延续。既然C2既不是C1同宗延续的儿子,也不是C3同宗继承的父亲,C2必定是C1和C3之间的异宗插入,说明C2-Tq是Dq。所以C2-Dq应该被独立成协作任务,为求解C3-Sq准备数据。这就证明了任务独立规则1的逆向成立。
顺便指出,接有Mq的中口不会再有独立的Rs。由于Dq是为Mq准备数据的,即Dq的求解结果将参与Mq的求解,Rs则属于Mq的一部分。
任务独立规则1中实际隐含了一个前提条件,即Dq中必须含有控制,否则就不会有Mq,因为Mq必须接于控制节点的中口。规则中的“Tq的根节点”既是Dq根节点也是Dq中的控制节点。不含控制的Dq是有的,其独立情况将在规则2中叙述。
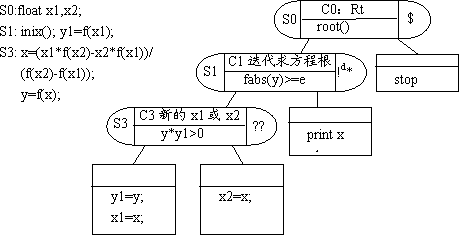
现在来看一个满足规则1的例子。博文《解一元高方程的任务树》中共有四棵作业树,根据它们之间的调用关系形成了图7.6的任务树。现在,我们将任务“Ini”和“Rt”的作业树合并,看会出现什么情况。如图8.2所示,合并后的作业树仍然可以正常运行,且可以得出正确的结果。这也正是任务独立的难点所在,并非一定要按规定独立出相应的任务后程序才能正确运行。我们是在讨论规范的树型软件程序设计,就必须按规定独立出所有的任务。显然,图8.2中C1-Tq是Dq,C2-Sq则是Mq。换句话说,C1是C0和C2之间的异宗插入。C0和C2是同宗的,C0是作业树的根节点,也是C2的祖宗。将C1-Dq独立成任务后,就形成了图7.2所示的Ini作业树。
图8.2 将任务Ini合并进Rt后的作业树
图8.2的例子可能会产生一种误会:C2-Sq也是一个独立的概念,也可以将其独立成任务,为什么将C1-Tq独立而不将C2-Sq独立呢?表面上看的确如此,将C2-Sq独立成任务root()函数后,图8.2的作业树所求解的Oq就是“选取x1和x2的初值”,根节点函数定义修改为init(),然后调用root()求解一元高次方程的根。显然,这是本末倒置,求方程的根才是目的,输入x1和x2的初值只是协助求根。问题的关键还不仅仅是本末倒置,而是根本解决不了异宗插入。图8.2中的这种误会,是因为Dq直接作为作业树根节点的左子树所造成的。如图8.1所示,如果将该图中C3-Sq独立成任务,C2-Tq仍然是存在于该作业树中的Dq。其结果是,C0、C1和C3本来是同宗的,现在却硬性地将C3-Sq割裂出去。而C2-Tq的求解根本与C3-Sq无关,现在却要在其求解结束后额外去调用C3-Sq的任务。由此可见,这样的Mq的独立不但没有解决异宗插入的问题,反而使同宗之间骨肉分离,将Oq的求解程序搅乱搅复杂了。
8.2.4 不含控制的Dq独立规则
图7.6的任务树中共有四个独立的任务:主任务Rt,协作任务Ini、Fx和Xp。我们已经找到了从Rt中独立出Ini的充要条件,剩下Fx和Xp被独立的条件是什么呢?这两个任务显然满足任务独立原理,应该被独立成任务。然而,我们又不能应用规则1来判断Fx或Xp是否是存在于作业树中的Dq,因为他们都是不含控制的任务,不满足规则1的前提条件。对于不含控制的Dq,我们可以按任务独立规则2来判断和处理。
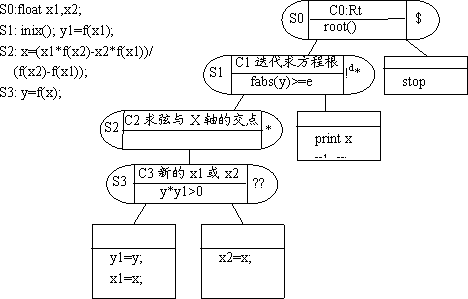
还是先看解一元高次方程的实例。仿照处理Rt和Ini的办法,将Xp的作业树合并进调用他的地方,看会出现什么情况。图8.3是将Xp合并进Rt后的作业树,将Fx合并进调用他的地方与此类似。将图8.3的作业树与图7.5中未合并的Rt作业树对比就可以看出,这两棵作业树几乎没有什么差异。再仔细一看才发现,节点C3的顺序部S3中的语句有所改变:语句x=xpoint()在图8.3中改成了x=(x1*f(x2)-x2*f(x1))/(f(x2)-f(x1)),即直接以原表达式替代了调用。由于任务Fx和Xp都只有一条顺序语句,所以将他们合并进调用他们的地方后仍然看不出Mq的存在。任务中不含控制,说明求解他的程序段中只有顺序语句,没有控制语句。由于没有控制语句,将其合并进作业树后也就不需要增加新的控制节点,作业树中也就不会出现Mq。
图8.3 将Xp合并进Rt后的作业树
我们知道,顺序节点是蜕化后的控制节点,也可以称顺序节点为不含控制的控制节点。我们将顺序节点画成控制节点的形状,令其逻辑表达式部为空,控制类型标志为“*”,顺序部存放原顺序节点中的语句,称这样的节点为“模拟控制节点”,如图8.4中的节点C2所示。图8.4是在图8.3的基础上增加了模拟控制节点C2后的作业树,这两个图中的作业树逻辑功能完全相同。节点C2的顺序部S2中存放了语句x=(x1*f(x2)-x2*f(x1))/(f(x2)-f(x1)),这条语句是从图8.3的节点C3的顺序部S3中移出来的。增加C2后,以C3为根的子树只好连接于C2的中口,所以C2的控制类型是“*”。将图8.3变换成图8.4是没有实际意义的,仅仅是为了说明:不含控制的Dq的存在本质上也会产Mq,Dq仍然是为了Mq的求解准备数据。这个结论适用于任意的顺序段,任意的顺序段都可以被独立成任务,这也满足任务独立原理。我们是在研究有意义的任务独立,当然不会随意地将一段程序独立成任务。对于不含控制的协作任务,我们有如下独立规则。
任务独立规则2:对于不含控制的独立概念,如果其在任务树中被重复使用,则认为该独立概念是Dq,应该将其独立成任务。
规则2也可以说是一种规定,既不需要证明也没有什么可解释的。解一元高次方程的任务树中,函数f(x)就是重复使用多次的独立概念,函数xpoint()则是只使用了一次的独立概念,所以前者必须被独立,后者可以独立也可以不独立。规则2是直接从任务独立原理归纳得出的,所以称被独立的任务为“独立概念”。当然也可以称之为Dq,图8.4中示意的C2就是插在C1和C3之间的Dq。将多次被使用的独立概念形成成任务,实际也适用于含有控制的独立概念。由于规则1专用于含有控制的任务独立,则规则2就专用于不含控制的任务独立。
图8.4 将图8.3中S3的一条语句放进模拟控制节点后的作业树
8.3 任务范畴的限定
综上所述,对于含有控制的Dq,采用任务独立规则1处理;对于不含控制的Dq,采用任务独立规则2处理。Dq只有含有或不含控制这两类,都可按任务独立规则处理,说明任务独立规则是完备的。
从任务的定义到任务独立原理与规则,本质上都是在讨论任务的作用范畴。本来,根据定义就应该可以严格任务的范畴,也就用不着讨论任务独立规则。然而,任务是以作业树来定义的,作业树的作用范畴并没严格的限定,所以任务的范畴也就无法限定。现在有了任务独立规则,其作用范畴就被严格限定了:任务内的所有Tq都必须是同宗的,凡插入的Dq都必须另行独立。于是,任务的定义可以修改为:
由同宗延续生成的作业树所表示的程序段称为任务。
显然,修改后的任务定义就相当严格了,作业树的功能就是求解一个任务。将插入的Dq都独立出去就限定了任务范畴的上限,与此同时也限定了任务范畴的下限。理论上,作业树中任意一条语句都可以被独立成任务,以至于可以将一个任务分割成许多任务。任务范畴的下限是由作业树中同宗延续的完整性所限定的。将同宗延续的操作独立出去,等价于割断了同宗延续,破坏了作业树的完整性。凡属作业树中同宗延续的操作,都不允许被独立。换句话说,作业树中除插入的Dq必须被独立成任务外,其它操作都不允许被独立成任务。
8.4 结束语
任务作为树型软件的一级模块,它的范畴比作业大一级,比后面将要定义的事件小一级。在传统的计算机软件结构中,任务应该是属于子程序或函数级的模块。
所谓子程序或函数,其基本思想都是将一个独立概念形成一段程序,以便单次或多次使用。在计算机程序设计的历史上,最早实现这种思想的做法被称为宏,随后才有子程序。函数的概念则是随着C语言的出现而被定义和使用的,C语言中没有子程序的定义,C函数兼有子程序的功能。通常认为,子程序和函数都可通过调用语句传递参数,但子程序不会返回值,函数则有返回值。
从C语言关于函数的定义可知,C函数的作用范畴并不受限,所以它涵盖了子程序,当然也涵盖了我们这里定义的任务。任务可以用C函数来表示,也可以用任何算法语言的子程序来表示。由任务的定义可知,它能且只能处理单宗的问题,一个任务中不允许有异宗语句的插入。所以,任务是范畴最小的函数或子程序,是最严谨最规范的函数或子程序。