FP-tree算法实现
支持度和置信度
严格地说Apriori和FP-Tree都是寻找频繁项集的算法,频繁项集就是所谓的“支持度”比较高的项集,下面解释一下支持度和置信度的概念。
设事务数据库为:
![]()
A E F G A F G A B E F G E F G
![]()
则{A,F,G}的支持度数为3,支持度为3/4。
{F,G}的支持度数为4,支持度为4/4。
{A}的支持度数为3,支持度为3/4。
{F,G}=>{A}的置信度为:{A,F,G}的支持度数 除以 {F,G}的支持度数,即3/4
{A}=>{F,G}的置信度为:{A,F,G}的支持度数 除以 {A}的支持度数,即3/3
强关联规则挖掘是在满足一定支持度的情况下寻找置信度达到阈值的所有模式。
FP-Tree算法
我们举个例子来详细讲解FP-Tree算法的完整实现。
事务数据库如下,一行表示一条购物记录:
![]()
牛奶,鸡蛋,面包,薯片 鸡蛋,爆米花,薯片,啤酒 鸡蛋,面包,薯片 牛奶,鸡蛋,面包,爆米花,薯片,啤酒 牛奶,面包,啤酒 鸡蛋,面包,啤酒 牛奶,面包,薯片 牛奶,鸡蛋,面包,黄油,薯片 牛奶,鸡蛋,黄油,薯片
![]()
我们的目的是要找出哪些商品总是相伴出现的,比如人们买薯片的时候通常也会买鸡蛋,则[薯片,鸡蛋]就是一条频繁模式(frequent pattern)。
FP-Tree算法第一步:扫描事务数据库,每项商品按频数递减排序,并删除频数小于最小支持度MinSup的商品。(第一次扫描数据库)
薯片:7鸡蛋:7面包:7牛奶:6啤酒:4 (这里我们令MinSup=3)
以上结果就是频繁1项集,记为F1。
第二步:对于每一条购买记录,按照F1中的顺序重新排序。(第二次也是最后一次扫描数据库)
![]()
薯片,鸡蛋,面包,牛奶 薯片,鸡蛋,啤酒 薯片,鸡蛋,面包 薯片,鸡蛋,面包,牛奶,啤酒 面包,牛奶,啤酒 鸡蛋,面包,啤酒 薯片,面包,牛奶 薯片,鸡蛋,面包,牛奶 薯片,鸡蛋,牛奶
![]()
第三步:把第二步得到的各条记录插入到FP-Tree中。刚开始时后缀模式为空。
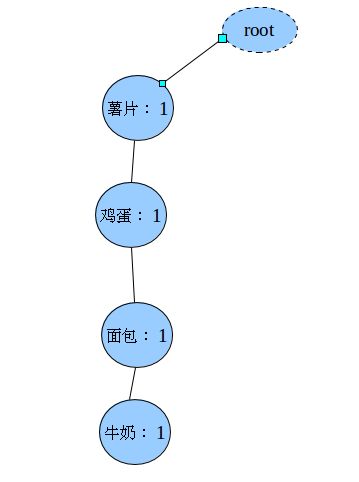
插入第一条(薯片,鸡蛋,面包,牛奶)之后
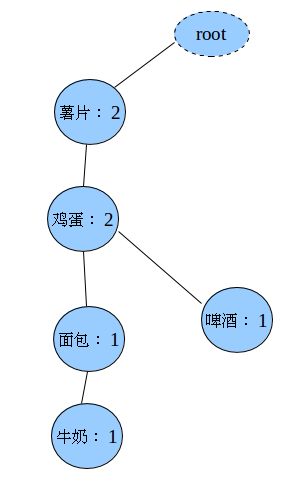
插入第二条记录(薯片,鸡蛋,啤酒)
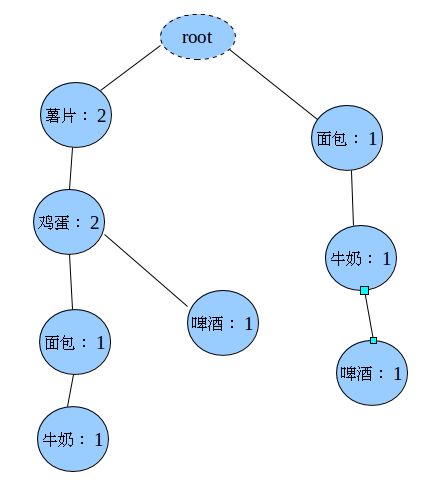
插入第三条记录(面包,牛奶,啤酒)
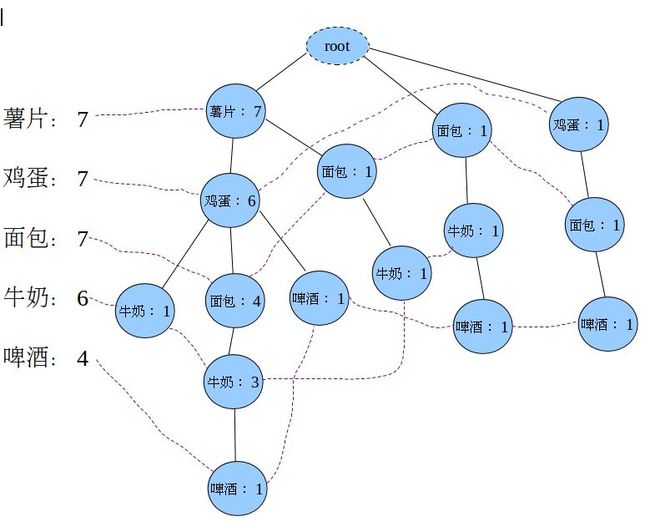
估计你也知道怎么插了,最终生成的FP-Tree是:
上图中左边的那一叫做表头项,树中相同名称的节点要链接起来,链表的第一个元素就是表头项里的元素。
如果FP-Tree为空(只含一个虚的root节点),则FP-Growth函数返回。
此时输出表头项的每一项+postModel,支持度为表头项中对应项的计数。
第四步:从FP-Tree中找出频繁项。
遍历表头项中的每一项(我们拿“牛奶:6”为例),对于各项都执行以下(1)到(5)的操作:
(1)从FP-Tree中找到所有的“牛奶”节点,向上遍历它的祖先节点,得到4条路径:
![]()
薯片:7,鸡蛋:6,牛奶:1薯片:7,鸡蛋:6,面包:4,牛奶:3薯片:7,面包:1,牛奶:1面包:1,牛奶:1
![]()
对于每一条路径上的节点,其count都设置为牛奶的count
![]()
薯片:1,鸡蛋:1,牛奶:1薯片:3,鸡蛋:3,面包:3,牛奶:3薯片:1,面包:1,牛奶:1面包:1,牛奶:1
![]()
因为每一项末尾都是牛奶,可以把牛奶去掉,得到条件模式基(Conditional Pattern Base,CPB),此时的后缀模式是:(牛奶)。
![]()
薯片:1,鸡蛋:1薯片:3,鸡蛋:3,面包:3薯片:1,面包:1面包:1
![]()
(2)我们把上面的结果当作原始的事务数据库,返回到第3步,递归迭代运行。
没讲清楚,你可以参考这篇博客,直接看核心代码吧:
![]()
public void FPGrowth(List<List<String>> transRecords,
List<String> postPattern,Context context) throws IOException, InterruptedException { // 构建项头表,同时也是频繁1项集
ArrayList<TreeNode> HeaderTable = buildHeaderTable(transRecords); // 构建FP-Tree
TreeNode treeRoot = buildFPTree(transRecords, HeaderTable); // 如果FP-Tree为空则返回
if (treeRoot.getChildren()==null || treeRoot.getChildren().size() == 0) return; //输出项头表的每一项+postPattern
if(postPattern!=null){ for (TreeNode header : HeaderTable) {
String outStr=header.getName(); int count=header.getCount(); for (String ele : postPattern)
outStr+="\t" + ele;
context.write(new IntWritable(count), new Text(outStr));
}
} // 找到项头表的每一项的条件模式基,进入递归迭代
for (TreeNode header : HeaderTable) { // 后缀模式增加一项
List<String> newPostPattern = new LinkedList<String>();
newPostPattern.add(header.getName()); if (postPattern != null)
newPostPattern.addAll(postPattern); // 寻找header的条件模式基CPB,放入newTransRecords中
List<List<String>> newTransRecords = new LinkedList<List<String>>();
TreeNode backnode = header.getNextHomonym(); while (backnode != null) { int counter = backnode.getCount();
List<String> prenodes = new ArrayList<String>();
TreeNode parent = backnode; // 遍历backnode的祖先节点,放到prenodes中
while ((parent = parent.getParent()).getName() != null) {
prenodes.add(parent.getName());
} while (counter-- > 0) {
newTransRecords.add(prenodes);
}
backnode = backnode.getNextHomonym();
} // 递归迭代 FPGrowth(newTransRecords, newPostPattern,context);
}
}
![]()
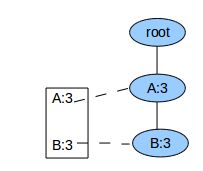
对于FP-Tree已经是单枝的情况,就没有必要再递归调用FPGrowth了,直接输出整条路径上所有节点的各种组合+postModel就可了。例如当FP-Tree为:
我们直接输出:
3 A+postModel
3 B+postModel
3 A+B+postModel
就可以了。
如何按照上面代码里的做法,是先输出:
3 A+postModel
3 B+postModel
然后把B插入到postModel的头部,重新建立一个FP-Tree,这时Tree中只含A,于是输出
3 A+(B+postModel)
两种方法结果是一样的,但毕竟重新建立FP-Tree计算量大些。
Java实现
FP树节点定义
+ View Code
挖掘频繁模式
+ View Code
输入文件
![]()
牛奶,鸡蛋,面包,薯片 鸡蛋,爆米花,薯片,啤酒 鸡蛋,面包,薯片 牛奶,鸡蛋,面包,爆米花,薯片,啤酒 牛奶,面包,啤酒 鸡蛋,面包,啤酒 牛奶,面包,薯片 牛奶,鸡蛋,面包,黄油,薯片 牛奶,鸡蛋,黄油,薯片
![]()
输出
![]()
6 薯片 鸡蛋5 薯片 面包5 鸡蛋 面包4 薯片 鸡蛋 面包5 薯片 牛奶5 面包 牛奶4 鸡蛋 牛奶4 薯片 面包 牛奶4 薯片 鸡蛋 牛奶3 面包 鸡蛋 牛奶3 薯片 面包 鸡蛋 牛奶3 鸡蛋 啤酒3 面包 啤酒
![]()
用Hadoop来实现
在上面的代码我们把整个事务数据库放在一个List<List<String>>里面传给FPGrowth,在实际中这是不可取的,因为内存不可能容下整个事务数据库,我们可能需要从关系关系数据库中一条一条地读入来建立FP-Tree。但无论如何 FP-Tree是肯定需要放在内存中的,但内存如果容不下怎么办?另外FPGrowth仍然是非常耗时的,你想提高速度怎么办?解决办法:分而治之,并行计算。
按照论文《FP-Growth 算法MapReduce 化研究》中介绍的方法,我们来看看语料中哪些词总是经常出现,一句话作为一个事务,这句话中的词作为项。
MR_FPTree.java
import imdm.bean.TreeNode;
import ioformat.EncryptFieInputFormat;
import java.io.IOException;
import java.text.SimpleDateFormat;
import java.util.ArrayList;
import java.util.Calendar;
import java.util.Collections;
import java.util.Comparator;
import java.util.LinkedHashMap;
import java.util.LinkedList;
import java.util.List;
import org.apache.hadoop.conf.Configuration;
import org.apache.hadoop.fs.FSDataInputStream;
import org.apache.hadoop.fs.FileSystem;
import org.apache.hadoop.fs.Path;
import org.apache.hadoop.io.IntWritable;
import org.apache.hadoop.io.LongWritable;
import org.apache.hadoop.io.Text;
import org.apache.hadoop.mapreduce.Job;
import org.apache.hadoop.mapreduce.Mapper;
import org.apache.hadoop.mapreduce.Reducer;
import org.apache.hadoop.mapreduce.lib.output.FileOutputFormat;
import org.apache.hadoop.util.GenericOptionsParser;
import org.apache.hadoop.util.LineReader;
import org.wltea.analyzer.dic.Dictionary;
import text.outservice.WordSegService;
public class MR_FPTree {
private static final int minSuport = 30; // 最小支持度
public static class GroupMapper extends
Mapper<LongWritable, Text, Text, Text> {
LinkedHashMap<String, Integer> freq = new LinkedHashMap<String, Integer>(); // 频繁1项集
org.wltea.analyzer.cfg.Configuration cfg = null;
Dictionary ikdict = null;
/**
* 读取频繁1项集
*/
@Override
public void setup(Context context) throws IOException {
// 初始化IK分词器
cfg = org.wltea.analyzer.cfg.DefaultConfig.getInstance();
ikdict = Dictionary.initial(cfg);
// 从HDFS文件读入频繁1项集,即读取IMWordCount的输出文件,要求已经按词频降序排好
Configuration conf = context.getConfiguration();
FileSystem fs = FileSystem.get(conf);
Calendar cad = Calendar.getInstance();
cad.add(Calendar.DAY_OF_MONTH, -1); // 昨天
SimpleDateFormat sdf = new SimpleDateFormat("yyyyMMdd");
String yes_day = sdf.format(cad.getTime());
Path freqFile = new Path("/dsap/resultdata/content/WordCount/"
+ yes_day + "/part-r-00000");
FSDataInputStream fileIn = fs.open(freqFile);
LineReader in = new LineReader(fileIn, conf);
Text line = new Text();
while (in.readLine(line) > 0) {
String[] arr = line.toString().split("\\s+");
if (arr.length == 2) {
int count = Integer.parseInt(arr[1]);
// 只读取词频大于最小支持度的
if (count > minSuport) {
String word = arr[0];
freq.put(word, count);
}
}
}
in.close();
}
@Override
public void map(LongWritable key, Text value, Context context)
throws IOException, InterruptedException {
String[] arr = value.toString().split("\\s+");
if (arr.length == 4) {
String content = arr[3];
List<String> result = WordSegService.wordSeg(content);
List<String> list = new LinkedList<String>();
for (String ele : result) {
// 如果在频繁1项集中
if (freq.containsKey(ele)) {
list.add(ele.toLowerCase()); // 如果包含英文字母,则统一转换为小写
}
}
// 对事务项中的每一项按频繁1项集排序
Collections.sort(list, new Comparator<String>() {
@Override
public int compare(String s1, String s2) {
return freq.get(s2) - freq.get(s1);
}
});
/**
* 比如对于事务(中国,人民,人民,广场),输出(中国,人民)、(中国,人民,广场)
*/
List<String> newlist = new ArrayList<String>();
newlist.add(list.get(0));
for (int i = 1; i < list.size(); i++) {
// 去除list中的重复项
if (!list.get(i).equals(list.get(i - 1))) {
newlist.add(list.get(i));
}
}
for (int i = 1; i < newlist.size(); i++) {
StringBuilder sb = new StringBuilder();
for (int j = 0; j <= i; j++) {
sb.append(newlist.get(j) + "\t");
}
context.write(new Text(newlist.get(i)),
new Text(sb.toString()));
}
}
}
}
public static class FPReducer extends
Reducer<Text, Text, Text, IntWritable> {
public void reduce(Text key, Iterable<Text> values, Context context)
throws IOException, InterruptedException {
List<List<String>> trans = new LinkedList<List<String>>(); // 事务数据库
while (values.iterator().hasNext()) {
String[] arr = values.iterator().next().toString()
.split("\\s+");
LinkedList<String> list = new LinkedList<String>();
for (String ele : arr)
list.add(ele);
trans.add(list);
}
List<TreeNode> leafNodes = new LinkedList<TreeNode>(); // 收集FPTree中的叶节点
buildFPTree(trans, leafNodes);
for (TreeNode leaf : leafNodes) {
TreeNode tmpNode = leaf;
List<String> associateRrule = new ArrayList<String>();
int frequency = 0;
while (tmpNode.getParent() != null) {
associateRrule.add(tmpNode.getName());
frequency = tmpNode.getCount();
tmpNode = tmpNode.getParent();
}
// Collections.sort(associateRrule); //从根节点到叶节点已经按F1排好序了,不需要再排序了
StringBuilder sb = new StringBuilder();
for (String ele : associateRrule) {
sb.append(ele + "|");
}
// 因为一句话可能包含重复的词,所以即使这些词都是从F1中取出来的,到最后其支持度也可能小于最小支持度
if (frequency > minSuport) {
context.write(new Text(sb.substring(0, sb.length() - 1)
.toString()), new IntWritable(frequency));
}
}
}
// 构建FP-Tree
public TreeNode buildFPTree(List<List<String>> records,
List<TreeNode> leafNodes) {
TreeNode root = new TreeNode(); // 创建树的根节点
for (List<String> record : records) { // 遍历每一项事务
// root.printChildrenName();
insertTransToTree(root, record, leafNodes);
}
return root;
}
// 把record作为ancestor的后代插入树中
public void insertTransToTree(TreeNode root, List<String> record,
List<TreeNode> leafNodes) {
if (record.size() > 0) {
String ele = record.get(0);
record.remove(0);
if (root.findChild(ele) != null) {
root.countIncrement(1);
root = root.findChild(ele);
insertTransToTree(root, record, leafNodes);
} else {
TreeNode node = new TreeNode(ele);
root.addChild(node);
node.setCount(1);
node.setParent(root);
if (record.size() == 0) {
leafNodes.add(node); // 把叶节点都放在一个链表中
}
insertTransToTree(node, record, leafNodes);
}
}
}
}
public static void main(String[] args) throws IOException,
InterruptedException, ClassNotFoundException {
Configuration conf = new Configuration();
String[] argv = new GenericOptionsParser(conf, args).getRemainingArgs();
if (argv.length < 2) {
System.err
.println("Usage: MR_FPTree EcryptedChartContent AssociateRules");
System.exit(1);
}
FileSystem fs = FileSystem.get(conf);
Path inpath = new Path(argv[0]);
Path outpath = new Path(argv[1]);
fs.delete(outpath, true);
Job FPTreejob = new Job(conf, "MR_FPTree");
FPTreejob.setJarByClass(MR_FPTree.class);
FPTreejob.setInputFormatClass(EncryptFieInputFormat.class);
EncryptFieInputFormat.addInputPath(FPTreejob, inpath);
FileOutputFormat.setOutputPath(FPTreejob, outpath);
FPTreejob.setMapperClass(GroupMapper.class);
FPTreejob.setMapOutputKeyClass(Text.class);
FPTreejob.setMapOutputValueClass(Text.class);
FPTreejob.setReducerClass(FPReducer.class);
FPTreejob.setOutputKeyClass(Text.class);
FPTreejob.setOutputKeyClass(IntWritable.class);
FPTreejob.waitForCompletion(true);
}
}
结束语
在实践中,关联规则挖掘可能并不像人们期望的那么有用。一方面是因为支持度置信度框架会产生过多的规则,并不是每一个规则都是有用的。另一方面大部分的关联规则并不像“啤酒与尿布”这种经典故事这么普遍。关联规则分析是需要技巧的,有时需要用更严格的统计学知识来控制规则的增殖。