PHP开发中的数据类型 ( 第3篇 ) :Heaps

参考自： http://www.sitepoint.com/data-structures-3/ （Published July 22, 2013）

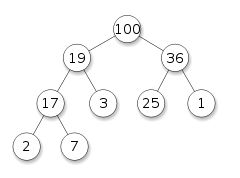
heaps 大概翻译成垛比较好吧，意思是许多、一堆（但不是stack的堆），heaps有几种类型，这里介绍一种叫做 binary maxheap : (binary：因为只有且必须有两个子节点、maxheap：因为任何父节点都比子节点的值大）。所以我的理解是它很像Tree，但是相比Tree而言，还有既定的顺序等。

Heaps也是table的一种形式，所以也有以下几种基本操作：

- 新建，即新建一个heap

- isEmpty，即检查是否heap为空
- insert，即向heap添加一个项目
- extract，即从heap中移除最顶端的那个项目

下面的代码实现了一个heap：

class BinaryHeap
{
    protected $heap;
 
    public function __construct() {
        $this->heap  = array();
    }
 
    public function isEmpty() {
        return empty($this->heap);
    }
 
    public function count() {
        // returns the heapsize
        return count($this->heap) - 1;
    }
 
    public function extract() {
        if ($this->isEmpty()) {
            throw new RunTimeException('Heap is empty');
        }
 
        // extract the root item
        $root = array_shift($this->heap);
 
        if (!$this->isEmpty()) {
            // move last item into the root so the heap is
            // no longer disjointed
            $last = array_pop($this->heap);
            array_unshift($this->heap, $last);
 
            // transform semiheap to heap
            $this->adjust(0);
        }
 
        return $root;
    }
 
    public function compare($item1, $item2) {
        if ($item1 === $item2) {
            return 0;
        }
        // reverse the comparison to change to a MinHeap!
        return ($item1 > $item2 ? 1 : -1);
    }
 
    protected function isLeaf($node) {
        // there will always be 2n + 1 nodes in the
        // sub-heap
        return ((2 * $node) + 1) > $this->count();
    }
 
    protected function adjust($root) {
        // we've gone as far as we can down the tree if
        // root is a leaf
        if (!$this->isLeaf($root)) {
            $left  = (2 * $root) + 1; // left child
            $right = (2 * $root) + 2; // right child
 
            // if root is less than either of its children
            $h = $this->heap;
            if (
              (isset($h[$left]) &&
                $this->compare($h[$root], $h[$left]) < 0)
              || (isset($h[$right]) &&
                $this->compare($h[$root], $h[$right]) < 0)
            ) {
                // find the larger child
                if (isset($h[$left]) && isset($h[$right])) {
                  $j = ($this->compare($h[$left], $h[$right]) >= 0)
                      ? $left : $right;
                }
                else if (isset($h[$left])) {
                  $j = $left; // left child only
                }
                else {
                  $j = $right; // right child only
                }
 
                // swap places with root
                list($this->heap[$root], $this->heap[$j]) =
                  array($this->heap[$j], $this->heap[$root]);
 
                // recursively adjust semiheap rooted at new
                // node j
                $this->adjust($j);
            }
        }
    }

    public function insert($item) {
        // insert new items at the bottom of the heap
        $this->heap[] = $item;
     
        // trickle up to the correct location
        $place = $this->count();
        $parent = floor($place / 2);
        // while not at root and greater than parent
        while (
          $place > 0 && $this->compare(
            $this->heap[$place], $this->heap[$parent]) >= 0
        ) {
            // swap places
            list($this->heap[$place], $this->heap[$parent]) =
                array($this->heap[$parent], $this->heap[$place]);
            $place = $parent;
            $parent = floor($place / 2);
        }
    }    
}

向结构中插入一些数据：

$heap = new BinaryHeap();
$heap->insert(19);
$heap->insert(36);
$heap->insert(54);
$heap->insert(100);
$heap->insert(17);
$heap->insert(3);
$heap->insert(25);
$heap->insert(1);
$heap->insert(67);
$heap->insert(2);
$heap->insert(7);

把heap打印出来的结果是下面这样的，完全没有任何规律：

Array
(
    [0] => 100
    [1] => 67
    [2] => 54
    [3] => 36
    [4] => 19
    [5] => 7
    [6] => 25
    [7] => 1
    [8] => 17
    [9] => 2
    [10] => 3
)

但是如果把项目extract操作一下，就按照顺序排列了：

while (!$heap->isEmpty()) {
    echo $heap->extract() . "n";
}  

100
67
54
36
25
19
17
7
3
2
1

PHP内置的heap： SplMaxHeap and SplMinHeap

class MyHeap extends SplMaxHeap
{
    public function compare($item1, $item2) {
        return (int) $item1 - $item2;
    }
}

PHP内置的heap： SplPriorityQueue

class PriQueue extends SplPriorityQueue
{
    public function compare($p1, $p2) {
        if ($p1 === $p2) return 0;
        // in ascending order of priority, a lower value
        // means higher priority
        return ($p1 < $p2) ? 1 : -1;
   }
}

$pq = new PriQueue();
$pq->insert('A', 4);
$pq->insert('B', 3);
$pq->insert('C', 5);
$pq->insert('D', 8);
$pq->insert('E', 2);
$pq->insert('F', 7);
$pq->insert('G', 1);
$pq->insert('H', 6);
$pq->insert('I', 0);
  
while ($pq->valid()) {
    print_r($pq->current());
    echo "n";
    $pq->next();
}

结果：

I
G
E
B
A
C
H
F
D 

// extract just the priority
$pq->setExtractFlags(SplPriorityQueue::EXTR_PRIORITY);
 
// extract both data and priority (returns an associative
// array for each element)
$pq->setExtractFlags(SplPriorityQueue::EXTR_BOTH);

EOF