数学算法在编程中的应用(初级)

--------------------------------华丽丽的分割线------------------------------------------------------

    ，写完的时候才忽然发现下面的图全部画反了，因为y=x*x的抛物线是开口向上的，而且顶点在(0,0)，所以当x>0时，始终，图形始终只有单调递增的那一半图形。不过毕竟是自己挤时间写的，再修改起来也费时费力，大家将就着看一下吧，把照片上 的图倒过来看就可以了，不过不影响算法的核心思想。

                             ---------------华丽丽的分割线-----------------------------

很久没写日志了，前几天一个技术群里的一个朋友提到了一些利用程序作图的问题，身为数学系，虽然数学不咋地，但总希望学的数学不能白费，经过一长段时间告诉他基本算法之后，自己就决定将一些想法记录下来。一来向大家分享经验，二来怕自己时隔太久之后忘记当时所理解的一些东西。当然，本人没学过计算机图形学，所以文章中也肯定会有不少的错误理解，希望朋友们积极指出，大家共同进步。

       问题：利用编程，在2D环境下，画出想要的曲线（可能是正余弦图像，也可能是抛物线或者其他曲线）。

       两点之间可以确定一条直线，但是两个点却永远没办法确定一条曲线，因为通过两个点的曲线有无数多个，进一步延伸的话，也可以推出即使是无数个点，也依然无法确定一条曲线。那么需要逻辑结构的编程语言究竟要怎样才能画出按照自己制定的规则来画出曲线呢？

      要想按照一定的规则来画曲线的必要条件就是必须知道这条曲线的代数方程式。 本例主要就画抛物线的算法来进行讲解。为方便起见，将采取最简单的抛物线方程式

       y=x*x (此处即x乘以x，也就是x的平方)。

该曲线的图像即为（0,0）坐标为顶点，开口向上的抛物线。

假设我们当前所使用的编程语言中(假设为OOP)有一个顶点对象Pointer以及将两个点连接成直线的函数，具体是什么函数我忘了，此处这个函数就用drawLine(pointer1, pointer2);来代替，其中参数pointer1, pointer2分别代表平面上的两个不同的点。pointer1的坐标值为(x1,y1),pointer2的坐标值为(x2,y2);

那么究竟怎样才能用编程语言来画出该抛物线的曲线呢？

之前我已经说过了，平面上的两个点可以确定一条直线，但是即便是无数多个点也无法确定一条曲线，而若想要画出我们想要的曲线就必须通过该曲线的代数方程了。目前我所知道的话曲线的方法就是将无数条直线按照抛物线方程式的规则首尾连接起来，直线越短，曲线越光滑，当每条直线的长度趋于0时，画出来的抛物线也是最光滑的曲线，否则，直线的长度越长，曲线的棱角越分明，这个长度达到一定程度时，就变成了类似于股票系统中的折线图了。如下图所示：

                                             图 1 

以下是算法思想和部分算法程序的示例，

首先，要有一个对象代表坐标轴上的某个点  Pointer(x,y)两个参数分别对应这个点坐标轴上的x值和y值。

其次需要一个函数能把两个不同的点组成一条直线drawLine (pointer1,pointer2);//参数分别对应两个不同的点。

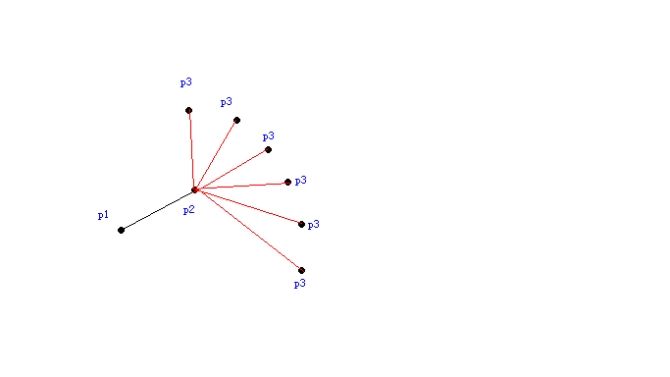
接下来要做的就是连接直线成曲线， 即将上一个连成直线的两个点的末尾那个点保留，作为下一条直线的起点，即初始时将p1与p2连接成直线，再之后将点p2作为直线p2、p3的起始点。那么我如何确定点p3呢？

 这就要用到曲线的方程式了，因为没有一定的规则限制的话点p3的位置是可以任意位置的，如下图：

所以我们要通过方程式来确定p3点的位置。

我们知道，抛物线的x值的范围是负无穷大到正无穷大，也就是说抛物线上各个点的x坐标是可以是实数系中的任意值，因此我们可以随意加减x的值都能保证这个点的x坐标在该抛物线的x坐标范围下。所以在此我们可以给x一个特定的增量值，这个增量值用单词increment来代替， 所以如果p1的点为(0,0)，那么p2的点的x坐标就为0+increment的值，

 设increment=0.5，

那么x2= 0 + 0.5 = 0.5

根据抛物线方程式y=x*x,

所以y2=0.5 * 0.5 = 0.25,即 p2点的坐标值为(0.5,0.25)    ①

同理可得

p3点的坐标为x3=0.5+increment = 1; y3 = 1*1 = 1;

即p3(1,1);

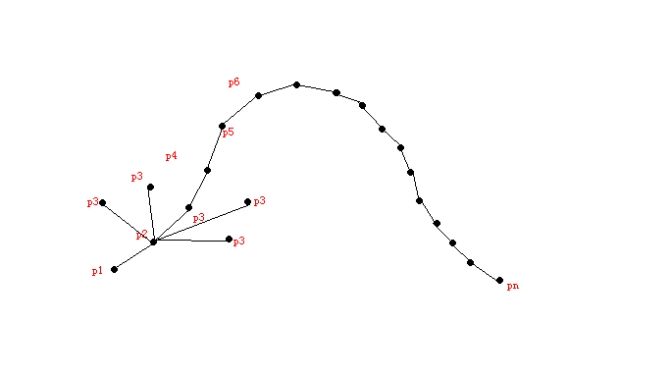
p4、p5、p6知道pn的点都能依次求出来，不过这不是做数学题，而是用编程语言去实现，所以这些繁杂而重复的计算就是计算机的任务了。下面开始涉及到编程。

我现在要用50条直线来组成一条抛物曲线，要做到这一点，我们就需要通过一个循环，来循环50次，从而生成51个点并依次组成直线。以下是一个for循环

var increment = 0.5                 //定义increment的值

var point1 = new Pointer(0,0)  //初始化第一个点

var point2 = new Pointer(0.5,0.25);       //new一个pointer对象，并按照式①计算的结果赋值

for(i=0;i<50;i++){//让程序循环50次

     point_tem = point2   //保存后面那个点，因为下一次循环是以上一条直线的末尾的点为起始点的

     drawLine (point1,point2);//画出一条直线，第一次循环时连接的是p1,p2点，第二次循环时连接的是p2、p3点

 

//以下程序，实际上，第一次循环时,此时是生成了点p3,然后重新进入循环圈并连接点p2,p3，成直线，第二次循环时生成了点p4,连接p3、p4成直线，依次类推。。。

     point2.x += increment;                  // point2.x是指取得对象point2的x坐标值，即设置当前point2的x的坐标值为 x + increment；

     point2.y = point2.x * point2.x ; 

}

如下图所示：

之后的图依次类推，顶点数足够多时，便会生成图1的那种图形。当然，这里的increment增量取值的大小可以影响生成的每条直线的长短，直线越短，顶点数越多，生成的曲线越趋于光滑。 当然， 上述程序算法中的50次循环，当increment增量值比较小时 可能只能画出来抛物曲线的一部分。

 

下面我们可以来做一下延伸。

因为以上的环境是在2D下的环境，那么3D下呢？

我们所在的世界除了时间以外，就是一个三维环境，很多时候我们看见远方的人影越来越靠近时，那个人会逐渐变大，在这个过程中实际上是人的大小并没有改变，而是他和我们之间的距离缩小了，所以给人的错觉是这个人不断变大。

那么计算机中的三维环境呢？

据我现在的理解中，在计算机中，计算机本身是一个平面的物体，它不可能无端的就从二维环境变成三维环境，这就牵扯到一个坐标的转化了，但是由于转化之后会从两个坐标值变为三个坐标值，这凭空多出来的z坐标值究竟怎么改变，这是我心里一直以来的一种疑问，也有可能是我在这一方面有很大的一块误解，希望知道的朋友能够指点一二。关于这一点，因为时间关系，没有找到一些很好的资料，等以后找到了我再做补充。在我的理解中，在计算机中， 因为一切都是虚拟的， 所以当一个物体存在于三维世界中时，它的大小会随着距离的远近而发生相应的变化

这种变化固然可以用数学方程式来表达，也就是说，在三维世界中，物体大小离我们远近的表现是不断改变物体的实际大小，而现实生活中物体的实际大小却是不会改变的。