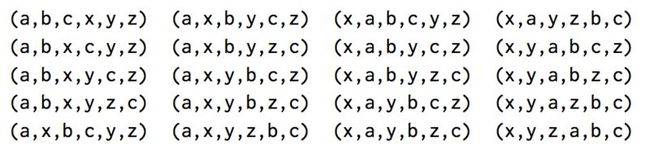SICP:Modularity, Objects, and State
3.1 Assignment and Local State
An object is said to "have state" if its behavior is influenced by its history.
In a system composed of many objects, the objects are rarely completely independent. Each may influence the states of others through interactions, which serve to couple the state variables of one object to those of other objects.Indeed, the view that a system is composed of separate objects is most useful when the state variables of the system can be grouped into closed coupled subsystems that are only loosely coupled to other subsystems.
For such a model to be modular, it should be decomposed into computational objects that model the actual objects in the system. Each computational object must have its own local state variables describing the actual object's state.Since the states of objects in the system being modeled change over time, the state variables of the corresponding computational objects must also change.
3.1.1 Local State Variables
(define balance 100)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
;75
(withdraw 25)
;50
(withdraw 25)
;"Insufficient funds"
(withdraw 60)
;35
(withdraw 15)
(set! <name> <new-value>)
(begin <exp1> <exp2> ... <expk>)
but balance is a global variable, so we should write code like that:
(define new-withdraw
(let ((balance 100))
(lambda (amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))))
;75
(new-withdraw 25)
;50
(new-withdraw 25)
;"Insufficient funds"
(new-withdraw 60)
;35
(new-withdraw 15)
(define (make-withdraw balance)
(lambda (amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds")))
(define W1 (make-withdraw 100))
(define W2 (make-withdraw 100))
;50
(W1 50)
;30
(W2 70)
;10
(W1 40)
;"Insufficient funds"
(W2 40)
(define (make-amount balance)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(define (dispatch m)
(cond ((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
(else (error "Unknown request: MAKE-ACCOUNT" m))))
dispatch)
(define acc (make-amount 100))
;50
((acc 'withdraw) 50)
;"Insufficient funds"
((acc 'withdraw) 60)
;90
((acc 'deposit) 40)
;30
((acc 'withdraw) 60) Each call to make-account sets up an environment with a local state variable balance.
3.1.2 The Benefits of Introducing Assignment
let's talk about the rand.
We can implement rand as a procedure with a local state variable x that is initialized to some fixed value random-init.Each call to rand computes rand-update of the current value of x, returns this as the random number, and also stores this as the new value of x:
(define rand (let ((x random-init))
(lambda ()
(set! x (rand-update x))
x)))
The Monte Carlo method consists of choosing sample experiments at random from a large set and then making deductions on the basis of the probabilities estimated from tabulating the results of those experiments.For example, we can approximate pi using the fact that 6 / pi^2 is the probability that two integers chosen at random will have no factors in common;
(define (estimate-pi trials)
(sqrt (/ 6 (monte-carlo trials cesaro-test))))
(define (cesaro-test trials)
(= (gcd (random trials) (random trials)) 1))
(define (monte-carlo trials experiment)
(define (iter trials-remaining trials-passed)
(cond ((= trials-remaining 0)
(/ trials-passed trials))
((experiment trials)
(iter (- trials-remaining 1)
(+ trials-passed 1)))
(else
(iter (- trials-remaining 1)
trials-passed))))
(iter trials 0))
;3.133682700398331
(estimate-pi 10000)
(define (estimate-pi trials)
(sqrt (/ 6 (random-gcd-test trials random-init))))
(define (random-gcd-test trials initial-x)
(define (iter trials-remaining trials-passed x)
(let ((x1 (rand-update x)))
(let ((x2 (rand-update x1)))
(cond ((= trials-remaining 0)
(/ trials-passed trials))
((= (gcd x1 x2) 1)
(iter (- trials-remaining 1)
(+ trials-passed 1)
x2))
(else
(iter (- trials-remaining 1)
trials-passed
x2))))))
(iter trials 0 initial-x))
3.1.3 The Costs of Introducing Assignment
Programming without any use of assignments, as we did throughout the first two chapters of this book, is accordingly known as functional programming.
To understand how assignment complicates matters, consider a simplified version of the make-withdraw procedure:
(define (make-simplified-withdraw balance)
(lambda (amount)
(set! balance (- balance amount))
balance))
(define W (make-simplified-withdraw 25))
;5
(W 20)
;-5
(W 10)
(define (make-decrementer balance)
(lambda (amount)
(- balance amount)))
(define D (make-decrementer 25))
;5
(D 20)
;15
(D 10)
((make-decrementer 25) 20) => ((lambda (amount) (- 25 amount)) 20) => (- 25 20) => 5
==>
((make-simplified-withdraw 25) 20) => ((lambda (amount) (set! balance (- 25 amount)) 25) 20)so the question is: balance is 5 or 25
Sameness and change
Suppose we can make-decrementer twice with the same argument to create two procedure:
(define D1 (make-decrementer 25)) (define D2 (make-decrementer 25))
Contrast this with making two calls to make-simplified-withdraw:
(define W1 (make-simplified-withdraw 25)) (define W2 (make-simplified-withdraw 25))
In general, we can determine that two apparently identical objects are indeed "the same one" only by modifying one object and then observing whether the other object has changed in the same way.But how can we tell if an object has "changed" other than by observing the "same" object twice and seeing whether some property of the object differs from one observation to the next?Thus, we cannot determine "change" without some a priori notion of "sameness", and we cannot determine sameness without observing the effects of change.
so we think that peter-acc and pail-acc have a bank account with $100 in it.
(define peter-acc (make-account 100)) (define paul-acc (make-account 100))
(define peter-acc (make-account 100)) (define paul-acc peter-acc)
Pitfalls of imperative programming
In addition to raising complications about computational models, programs written in imperative style are susceptible to bugs that cannot occur in functional programs.consider the procedure:
(define (factorial n)
(define (iter product counter)
(if (> counter n)
product
(iter (* counter product) (+ counter 1))))
(iter 1 1))
(define (factorial-2 n)
(let ((product 1)
(counter 1))
(define (iter)
(if (> counter n)
product
(begin (set! product (* counter product))
(set! counter (+ counter 1))
(iter))))
(iter)))
(set! counter (+ counter 1)) (set! product (* counter product))
3.2 The Environment Model of Evaluation
To apply a compound procedure to arguments, evaluate the body of the procedure with each formal parameter replaced by the corresponding argument.
Once we admit assignment into our programming language, such a definition is no longer adequate, that a variable can no longer be considered to be merely a name for a value.Rather, a variable must somehow designate a "place" in which values can be stored. In our new model of evaluation, these place will be maintained in structures called environments.
An environment is a sequence of frames.Each frame is a table(possibly empty) of bindings, which associate variable names with their corresponding value.Each frame also has a pointer to its enclosing environment, unless, for the purposes of discussion, the frame is considered to be global.
3.2.1 The Rules for Evaluation
To evaluate a combination:
1. Evaluate the subexpressions of the combination.
2. Apply the value of the operator subexpression to the values of the operand subexpressions.
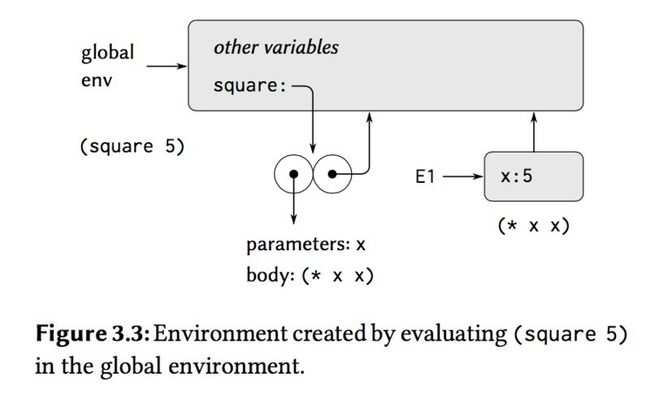
consider the procedure definition:
(define (square x) (* x x))
(define square (lambda (x) (* x x)))
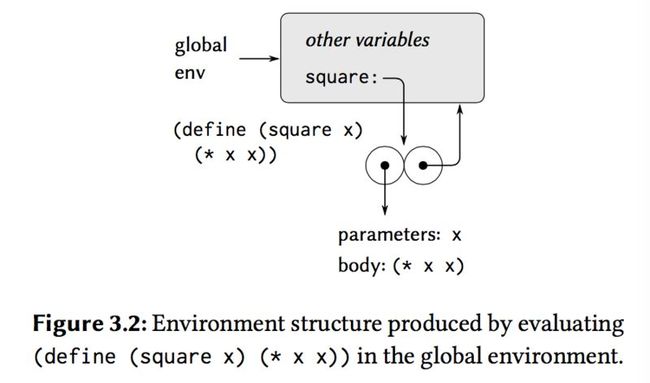
to the Figure 3.2, we can think that:
1. square is a procedure(a variable in the global environment, point to the procedure body (* x x))
2. as square point to the procedure body, when give the argument x, the procedure will return to the environment as a expression(like Figure3.3)
The environment model of procedure application can be summarized by two rules:
1. A procedure object is applied to a set of arguments by constructing a frame, binding the formal parameters of the procedure to the arguments of the call, and then evaluating the body of the procedure in the context of the new environment constructed. The new frame has as its enclosing environment the environment part of the procedure object being applied.
2. A procedure is created by evaluating a lambda-expression relative to a given environment. The resulting procedure object is a pair consisting of the text of the lambda-expression and a pointer to the environment in which the procedure was created.
Evaluating the expression (set! <variable> <value>) in some environment locates the binding to indicate the new value.That is, one finds the first frame in the environment that contains a binding for the variable and modifies that frame. If the variable is unbound in the environment, then set! signals an error.
3.2.2 Applying Simple Procedures
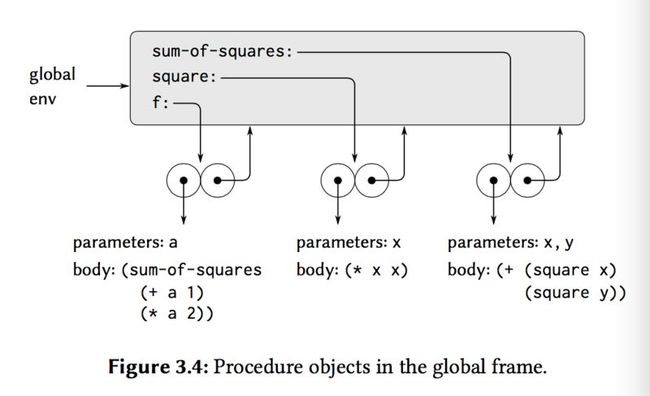
we think the procedure:
(define (square x) (* x x)) (define (sum-of-squares x y) (+ (square x) (square y))) (define (f a) (sum-of-squares (+ a 1) (* a 2)))
but the environment created by evaluating (f 5) like that:
3.2.3 Frames as the Repository of Local State
let's consider the procedure:
(define (make-withdraw balance)
(lambda (amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds")))
(define W1 (make-withdraw 100))
(W1 50) 50
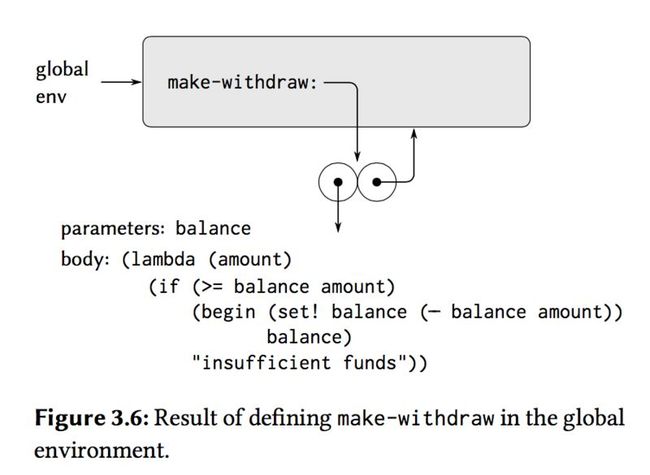
The interesting part of the computation happens when we apply the procedure make-withdraw to an argument:
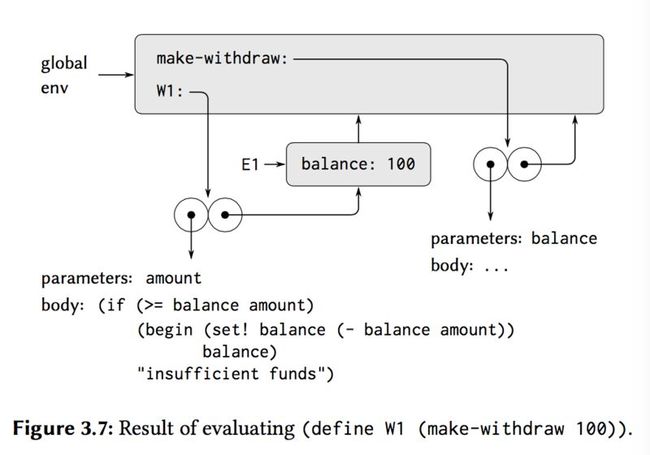
(define W1 (make-withdraw 100))
The resulting procedure object is the value returned by the call to make-withdraw.This is bound to W1 in the global environment, since the define itself is being evaluated in the global environment:
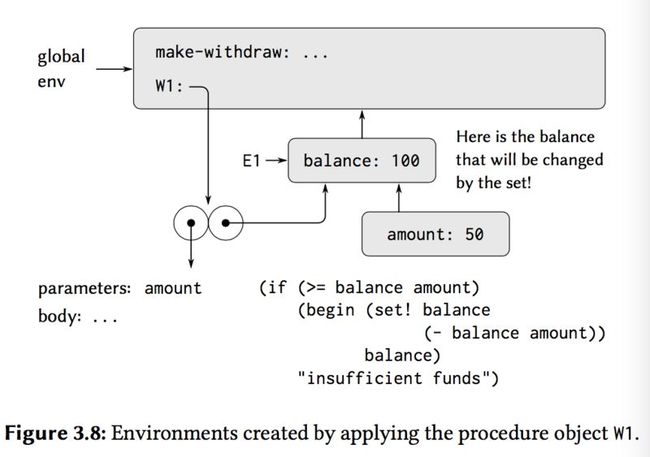
Now we can analyze what happens when W1 is applied to an argument:
(W1 50) 50
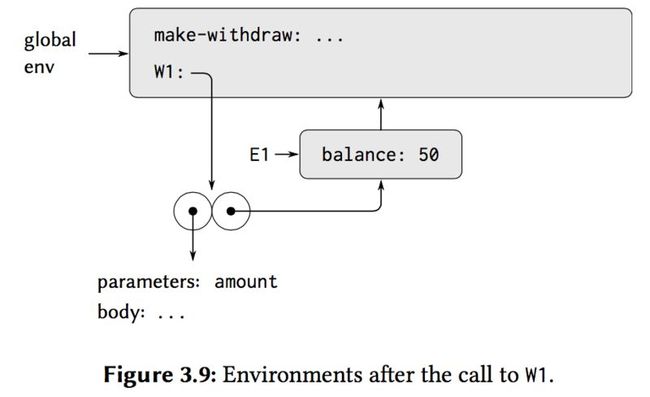
When the set! is executed, the binding of balance in E1 is changed.At the completion of the call to W1, balance is 50, and the frame that contains balance is still pointed to by the procedure object W1.The frame that binds amount(in which we executed the code that changed balance) is no longer relevant, since the procedure call that constructed it has terminated, and there are no pointers to that frame from other parts of the environment.The next time W1 is called, this will build a new frame that binds amount and whose enclosing environment is E1.We see that E1 serves as the "place" that holds the local state variable for the procedure object W1:
that is why W1 and W2 is different:
(define W1 (make-withdraw 100)) (define W2 (make-withdraw 100))

3.2.4 Internal Definitions
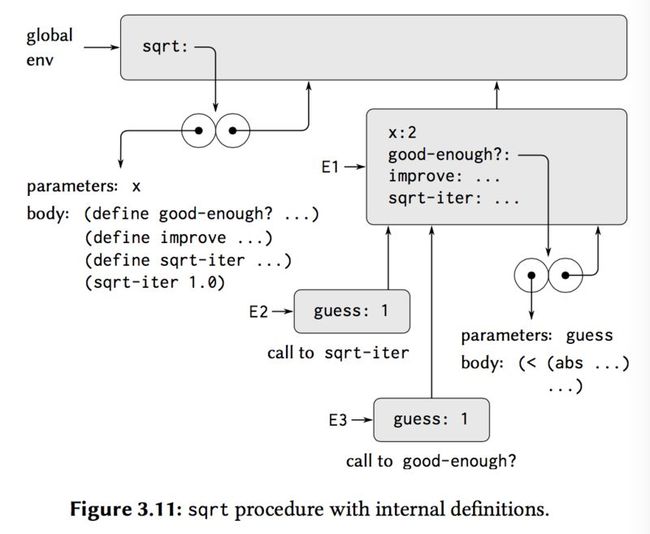
the sqrt procedure:
(define (sqrt x)
(define (good-enough? guess)
(< (abs (- (square guess) x)) 0.001))
(define (improve guess)
(average guess (/ x guess)))
(define (sqrt-iter guess)
(if (good-enough? guess)
guess
(sqrt-iter (improve guess))))
(sqrt-iter 1.0))
The environment model thus explains the two key properties that make local procedure definitions a useful technique for modularizing programs:
1. The names of the local procedures do not interfere with names external to the enclosing procedure, because the local procedure names will be bound in the frame that the procedure creates when it is run, rather than being bound in the global environment.
2. The local procedures can access the arguments of the enclosing procedure, simply by using parameter names as free variables. This is because the body of the local procedure is evaluated in an environment that is subordinate to the evaluation environment for the enclosing procedure.
3.3 Modeling with Mutable Data
3.3.1 Mutable List Structure
just think that we have: set-car! and set-cdr! procedure, we can define cons like that:
(define (cons x y)
(let ((new (get-new-pair)))
(set-car! new x)
(set-cdr! new y)
new))
(define x '((a b) c d)) (define y '(e f)) (set-car! x y) ;((e f) c d) x ;((e f) e f) (set-cdr! x y) x
let us consider two variable:
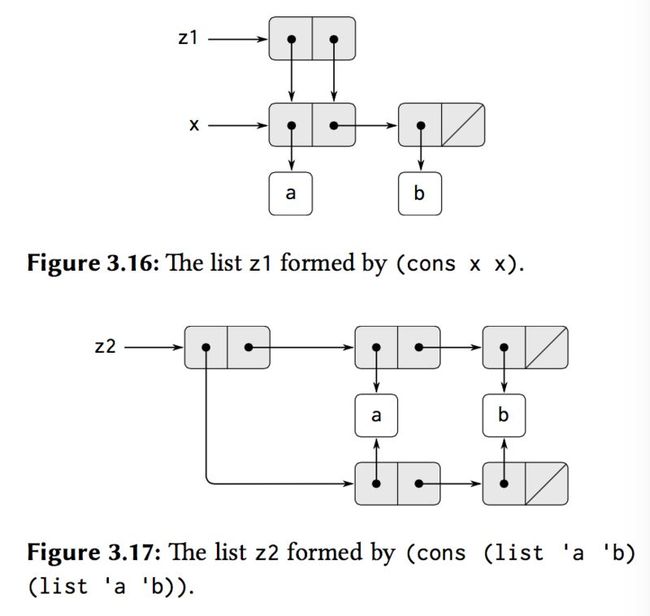
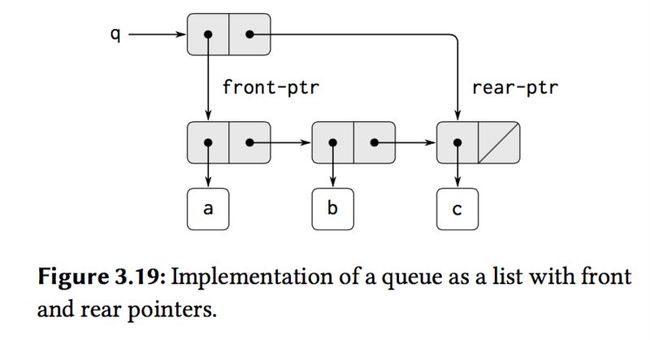
(define x '(a b)) (define z1 (cons x x)) (define z2 (cons '(a b) '(a b)))
so (car z1) == (cdr z1), but (car z2) != (cdr z2):
(define x '(a b)) (define z1 (cons x x)) (define z2 (cons '(a b) '(a b))) ;#t (eq? (car z1) (cdr z1)) ;#f (eq? (car z2) (cdr z2))
(define x '(a b)) (define z1 (cons x x)) (define z2 (cons '(a b) '(a b))) (define (set-to-wow! x) (set-car! (car x) 'wow) x) ;((a b) a b) z1 ;((wow b) wow b) (set-to-wow! z1) ;((a b) a b) z2 ;((wow b) a b) (set-to-wow! z2)
3.3.2 Representing Queues
A queue is a sequence in which items are inserted at one end(called the rear of the queue) and deleted from the other end(the front).
In terms of data abstraction, we can regard a queue as defined by the following set of operation:
1. a constructor: (make-queue) returns an empty queue(a queue containing no items)
2. two selectors:
(empty-queue? <queue>) tests if the queue is empty.
(front-queue <queue>) returns the object at the front of the queue, signaling an error if the queue is empty;it does not modify the queue.
3. two mutators:
(insert-queue! <queue> <item>) inserts the item at the rear of the queue and returns the modified queue as its value.
(delete-queue! <queue>) removes the item at the front of the queue and returns the modified queue as its value, signaling an error if the queue is empty before the deletion.
A queue can not be represented as an ordinary list, just think that we insert an item, we should do:(append queue item), we delete an item, we should do:(cdr queue;return (car queue)), but they are using n steps!
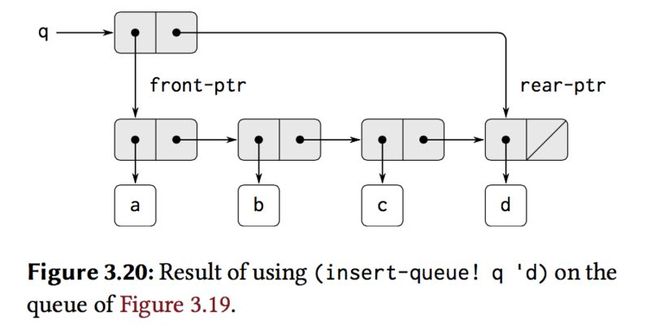
A queue is represented as a pair of pointers, front-ptr and rear-ptr, which indicate the first and last pairs in an ordinary list.
so the queue can define as follow:
(define (front-ptr queue) (car queue)) (define (rear-ptr queue) (cdr queue)) (define (set-front-ptr! queue item) (set-car! queue item)) (define (set-rear-ptr! queue item) (set-cdr! queue item))
(define (empty-queue? queue) (null? (front-ptr queue)))
(define (make-queue) (cons '() '()))
(define (front-queue queue)
(if (empty-queue? queue)
(error "FRONT called with an empty queue" queue)
(car (front-ptr queue))))
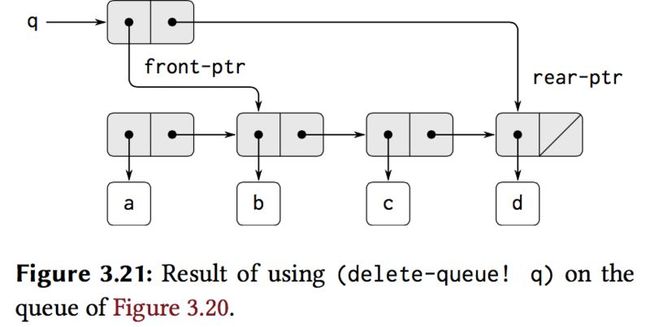
We first create a new pair whose car is the item to be inserted and whose cdr is the empty list.If the queue was initially empty, we set the front and rear pointers of the queue to this new pair.Otherwise, we modify the final pair in the queue to point to the new pair, and also set the rear pointer to the new pair:
(define (insert-queue! queue item)
(let ((new-pair (cons item '())))
(cond ((empty-queue? queue)
(set-front-ptr! queue new-pair)
(set-rear-ptr! queue new-pair)
queue)
(else
(set-cdr! (rear-ptr queue) new-pair)
(set-rear-ptr! queue new-pair)
queue))))
(define (delete-queue! queue)
(cond ((empty-queue? queue)
(error "DELETE! called with an empty queue" queue))
(else (set-front-ptr! queue (cdr (front-ptr queue)))
queue)))
3.3.3 Representing Tables
One-dimensional tables
We first consider a one-dimensional table, in which each value is stored under a single key.We implement the table as a list of records, each of which is implemented as a pair consisting of a key and the associated value.
we can define lookup to find the key-value:
(define (lookup key table)
(let ((record (assoc-new key (cdr table))))
(if record
(cdr record)
false)))
(define (assoc-new key records)
(cond ((null? records) false)
((equal? key (caar records)) (car records))
(else (assoc-new key (cdr records)))))
We can write the insert! function:
(define (insert! key value table)
(let ((record (assoc key (cdr table))))
(if record
(set-cdr! record value)
(set-cdr! table
(cons (cons key value)
(cdr table)))))
'ok)
(define (make-table) (list '*table*))
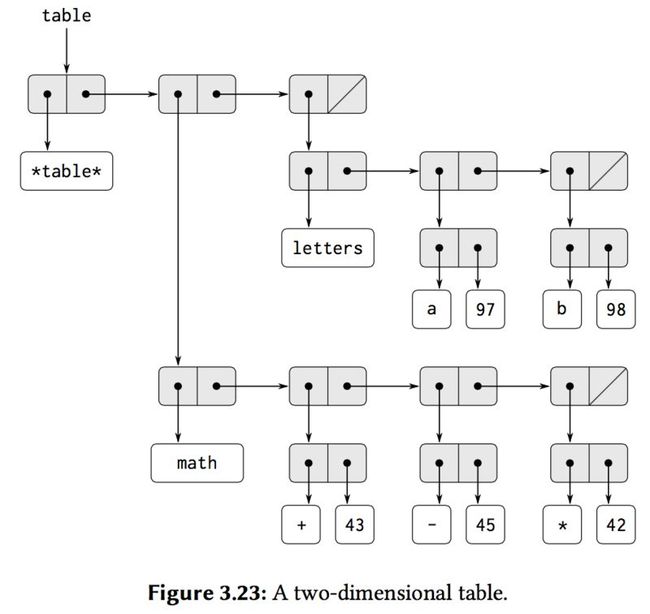
In a two-dimensional table, each value is indexed by two keys.
When we look up an item, we use the first key to identify the correct subtable. Then we use the second key to identify the record within the subtable:
(define (lookup key-1 key-2 table)
(let ((subtable
(assoc key-1 (cdr table))))
(if subtable
(let ((record
(assoc key-2 (cdr subtable))))
(if record
(cdr record)
false))
false)))
(define (insert! key-1 key-2 value table)
(let ((subtable (assoc key-1 (cdr table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(set-cdr! record value)
(set-cdr! subtable
(cons (cons key-2 value)
(cdr subtable)))))
(set-cdr! table
(cons (list key-1
(cons key-2 value))
(cdr table)))))
'ok)
(define (make-table)
(let ((local-table (list '*table*)))
(define (lookup key-1 key-2)
(let ((subtable
(assoc key-1 (cdr local-table))))
(if subtable
(let ((record
(assoc key-2 (cdr subtable))))
(if record (cdr record) false))
false)))
(define (insert! key-1 key-2 value)
(let ((subtable
(assoc key-1 (cdr local-table))))
(if subtable
(let ((record
(assoc key-2 (cdr subtable))))
(if record
(set-cdr! record value)
(set-cdr! subtable
(cons (cons key-2 value)
(cdr subtable)))))
(set-cdr! local-table
(cons (list key-1 (cons key-2 value))
(cdr local-table)))))
'ok)
(define (dispatch m)
(cond ((eq? m 'lookup-proc) lookup)
((eq? m 'insert-proc) insert!)
(else (error "Unknown operation: TABLE" m))))
dispatch)) Using make-table, we could implement the get and put operations:
(define operation-table (make-table)) (define get (operation-table 'lookup-proc)) (define put (operation-table 'insert-proc))
3.3.4 A Simulator for Digital Circuits
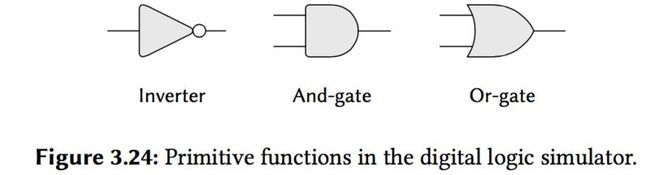
In this section we design a system for performing digital logic simulations.This system typifies a kind of program called an event-driven simulation, in which action("events") trigger further events that happen at a later time, which in turn trigger more events, and so on.
A digital signal may at any moment have only one of two possible values, 0 and 1.
We will now build a program for modeling the digital logic circuits we wish to study.One basic element of our simulation will be a procedure make-wire, which constructs wires.
(define a (make-wire)) (define b (make-wire)) (define c (make-wire)) (define d (make-wire)) (define e (make-wire)) (define s (make-wire))
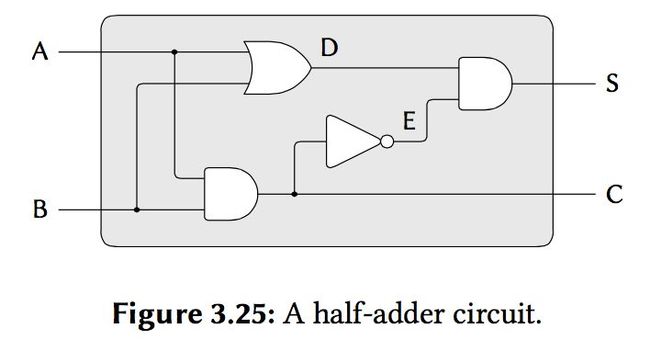
we first finish: A half-adder circuit
we could use or-gate, and-gate, inverter to define a procedure half-adder:
(define (half-adder a b s c)
(let ((d (make-wire)) (e (make-wire)))
(or-gate a b d)
(and-gate a b c)
(inverter c e)
(and-gate d e s)
'ok))
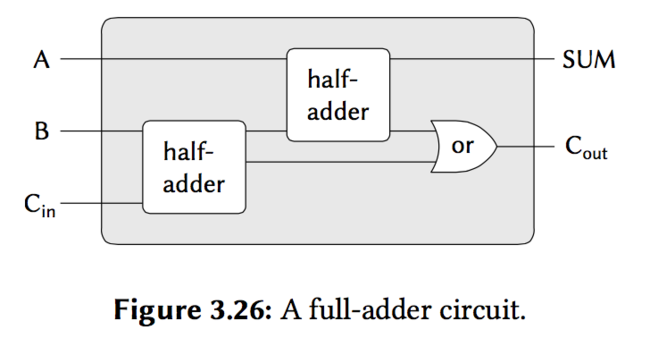
we could write the code:
(define (full-adder a b c-in sum c-out)
(let ((s (make-wire)) (c1 (make-wire)) (c2 (make-wire)))
(half-adder b c-in s c1)
(half-adder a s sum c2)
(or-gate c1 c2 c-out)
'ok))
The primitive function boxes implement the "forces" by which a change in the signal on one wire influences the signals on other wires. To build function boxes, we use the following operations on wires:
1. (get-signal <wire>)
return the current value of the signal on the wire.
2. (set-signal! <wire> <new value>)
change the value of the signal on the wire to the new value.
3. (add-action! <wire> <procedure of no arguments>)
asserts that the designated procedure should be run whenever the signal on the wire changes value. Such procedures are the vehicles by which changes in the signal value on the wire are communicated to other wires.
In addition, we will make use of a procedure after-delay that takes a time delay and a procedure to be run and executes the given procedure after the given delay.
(define (inverter input output)
(define (invert-input)
(let ((new-value (logical-not (get-signal input))))
(after-delay inverter-delay
(lambda () (set-signal! output new-value)))))
(add-action! input invert-input) 'ok)
(define (logical-not s)
(cond ((= s 0) 1)
((= s 1) 0)
(else (error "Invalid signal" s))))
(define (and-gate a1 a2 output)
(define (and-action-procedure)
(let ((new-value
(logical-and (get-signal a1) (get-signal a2))))
(after-delay
(lambda () (set-signal! output new-value)))))
(add-action! a1 and-action-procedure)
(add-action! a2 and-action-procedure)
'ok)
(define (logical-and s1 s2)
(cond ((and (= s1 1) (= s2 1)) 1)
((or (and (= s1 1) (= s2 0))
(and (= s1 0) (= s2 1))
(and (= s1 0) (= s2 0))) 0)
(else (error "Invalid signal" s1 s2))))
(define (or-gate a1 a2 output)
(define (or-action-procedure)
(let ((new-value
(logical-or (get-signal a1) (get-signal a2))))
(after-delay
(lambda () (set-signal! output new-value)))))
(add-action! a1 or-action-procedure)
(add-action! a2 or-action-procedure)
'ok)
(define (logical-or s1 s2)
(cond ((and (= s1 0) (= s2 0)) 0)
((or (and (= s1 1) (= s2 0))
(and (= s1 0) (= s2 1))
(and (= s1 1) (= s2 1))) 1)
(else (error "Invalid signal" s1 s2))))
Representing wires
A wire in our simulation will be a computational object with two local state variable:a signal-value(initially taken to be 0) and a collection of action-procedures to be run when the signal changes value.
(define (make-wire)
(let ((signal-value 0) (action-procedures '()))
(define (set-my-signal! new-value)
(if (not (= signal-value new-value))
(begin (set! signal-value new-value)
(call-each action-procedures))
'done))
(define (accept-action-procedure! proc)
(set! action-procedures
(cons proc action-procedures))
(proc))
(define (dispatch m)
(cond ((eq? m 'get-signal) signal-value)
((eq? m 'set-signal!) set-my-signal!)
((eq? m 'add-action!) accept-action-procedure!)
(else (error "Unknown operation: WIRE" m))))
dispatch))
(define (call-each procedures)
(if (null? procedures)
'done
(begin ((car procedures))
(call-each (cdr procedures)))))
(define (get-signal wire) (wire 'get-signal)) (define (set-signal! wire new-value) ((wire 'set-signal!) new-value)) (define (add-action! wire action-procedure) ((wire 'add-action!) action-procedure))The wires are shared among the various devices that have been connected to them. Thus, a change made by an interaction with one device will affect all the other devices attached to the wire.The wire communicates the change to its neighbors by calling the action procedures provided to it when the connections were established.
The agenda
The only thing needed to complete the simulator is after-delay. The idea here is that we maintain a data structure, called an agenda, that contains a schedule of things to do. The following operations are defined for agendas:
1. (make-agenda) return a new empty agenda
2. (empty-agenda? <agenda>) is true if the specified agenda is empty.
3. (first-agenda-item <agenda>) returns the first item on the agenda.
4. (remove-first-agenda-item! <agenda>) modifies the agenda by removing the first item.
5. (add-to-agenda! <time> <action> <agenda>) modifies the agenda by adding the given action procedure to be run at the specified time.
6. (current-time <agenda>) returns the current simulation time.
The procedure after-delay adds new elements to the-agenda:
(define (after-delay delay action)
(add-to-agenda! (+ delay (current-time the-agenda))
action
the-agenda))
(define (propagate)
(if (empty-agenda? the-agenda)
'done
(let ((first-item (first-agenda-item the-agenda)))
(first-item)
(remove-first-agenda-item! the-agenda)
(propagate))))
Implementing the agenda
The agenda is made up of time segments. Each time segment is a pair consisting of a number(the time) and a queue that holds the procedures that are scheduled to be run during that time segment.
(define (make-time-segment time queue) (cons time queue)) (define (segment-time s) (car s)) (define (segment-queue s) (cdr s))
(define (make-agenda) (list 0)) (define (current-time agenda) (car agenda)) (define (set-current-time! agenda time) (set-car! agenda time)) (define (segments agenda) (cdr agenda)) (define (set-segments! agenda segments) (set-cdr! agenda segments)) (define (first-segment agenda) (car (segments agenda))) (define (rest-segments agenda) (cdr (segments agenda))) (define (empty-agenda? agenda) (null? (segments agenda)))
(define (add-to-agenda! time action agenda)
(define (belong-before? segments)
(or (null? segments)
(< time (segment-time (car segments)))))
(define (make-new-time-segment time action)
(let ((q (make-queue)))
(insert-queue! q action)
(make-time-segment time q)))
(define (add-to-segments! segments)
(if (= (segment-time (car segments)) time)
(insert-queue! (segment-queue (car segments))
action)
(let ((rest (cdr segments)))
(if (belongs-before? rest)
(set-cdr!
segments
(cons (make-new-time-segment time action)
(cdr segments)))
(add-to-segments1 rest)))))
(let ((segments (segments agenda)))
(if (belong-before? segments)
(set-segments!
agenda
(cons (make-new-time-segment time action)
segments))
(add-to-segments! segments))))
(define (remove-first-agenda-item! agenda)
(let ((q (segment-queue (first-segment agenda))))
(delete-queue! q)
(if (empty-queue? q)
(set-segments! agenda (rest-segments agenda)))))
(define (first-agenda-item agenda)
(if (empty-agenda? agenda)
(error "Agenda is empty:FIRST-AGENDA-ITEM")
(let ((first-seg (first-segment agenda)))
(set-current-time! agenda
(segment-time first-seg))
(front-queue (segment-queue first-seg)))))
the whole code in:
https://github.com/leicj/learning-SICP/blob/master/chapter3/3.31
3.3.5 Propagation of Constraints
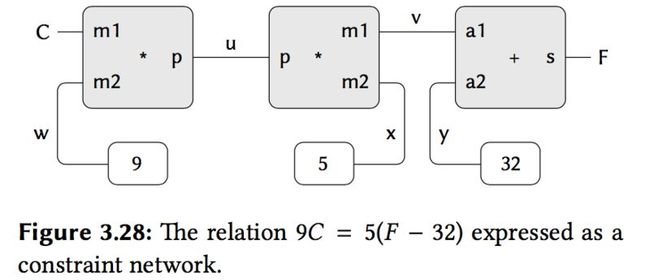
In this section, we sketch the design of a language that enables us to work in terms of relations themselves.The primitive elements of the language are primitive constraints, which state that certain relations hold between quantities.For example, (adder a b c) specifies that the quantities a, b, and c must be related by the equation a + b = c, (multiplier x y z) expresses the constraint xy = z, and (constant 3.14 x) says that the value of x must be 3.14.
We combine constraints by constructing constraint networks, in which constraints are joined by connectors. A connector is an object that "holds" a value that may participate in one or more constraints.For example:
9C = 5(F - 32)
the network is:
Computation by such a network proceeds as follows: When a connector is given a value(by the user or by a constraint box to which it is linked), it awakens all of its associated constraints(except for the constraint that just awakened it) to inform them that it has a value.Each awakened constraint box then polls its connectors to see if there is enough information to determine a value for a connector.If so, the box sets that connector, which then awakens all of its associated constraints, and so on.
Implementing the constraint system
The basic operations on connectors are the following:
1. (has-value? <connector>) tells whether the connector has a value
2. (get-value <connector>) returns the connector's current value.
3. (set-value! <connector> <new-value> <informant>) indicates that the informant is requesting the connector to set its value to the new value.
4. (forget-value! <connector> <retractor>) tells the connector that the retractor is requesting it to forget its value.
5. (connect <connector> <new-constraint>) tells the connector to participate in the new constraint.
the adder procedure:
(define (adder a1 a2 sum)
(define (process-new-value)
(cond ((and (has-value? a1) (has-value? a2))
(set-value! sum
(+ (get-value a1) (get-value a2))
me))
((and (has-value? a1) (has-value? sum))
(set-value! a2
(- (get-value sum) (get-value a1))
me))
((and (has-value? a2) (has-value? sum))
(set-value! a1
(- (get-value sum) (get-value a2))
me))))
(define (process-forget-value)
(forget-value! sum me)
(forget-value! a1 me)
(forget-value! a2 me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value) (process-new-value))
((eq? request 'I-lost-my-value) (process-forget-value))
(else (error "Unknown request: ADDER" request))))
(connect a1 me)
(connect a2 me)
(connect sum me)
me)
The following "syntax interfaces" are used in conjunction with the dispatch:
(define (inform-about-value constraint) (constraint 'I-have-a-value)) (define (inform-about-no-value constraint) (constraint 'I-lost-my-value))
(define (multiplier m1 m2 product)
(define (process-new-value)
(cond ((or (and (has-value? m1) (= (get-value m1) 0))
(and (has-value? m2) (= (get-value m2) 0)))
(set-value! product 0 me))
((and (has-value? m1) (has-value? m2))
(set-value! product
(* (get-value m1) (get-value m2))
me))
((and (has-value? product) (has-value? m1))
(set-value! m2
(/ (get-value product)
(get-value m1))
me))
((and (has-value? product) (has-value? m2))
(set-value! m1
(/ (get-value product)
(get-value m2))
me))))
(define (process-forget-value)
(forget-value! product me)
(forget-value! m1 me)
(forget-value! m2 me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value) (process-new-value))
((eq? request 'I-lost-my-value) (process-forget-value))
(else (error "Unknown request: MULTIPLIER" request))))
(connect m1 me)
(connect m2 me)
(connect product me)
me)
(define (constant value connector)
(define (me request)
(error "Unknown request: CONSTANT" request))
(connect connector me)
(set-value! connector value me)
me)
(define (probe name connector)
(define (print-probe value)
(newline)(display "Probe: ")(display name)
(display " = ")(display value))
(define (process-new-value)
(print-probe (get-value connector)))
(define (process-forget-value) (print-probe "?"))
(define (me request)
(cond ((eq? request 'I-have-a-value) (process-new-value))
((eq? request 'I-lost-my-value) (process-forget-value))
(else (error "Unknown request: PROBE" request))))
(connect connector me)
me)
A connector is represented as a procedural object with local state variables value, the current value of the connector;informant, the object that set the connector's value; and constraints, a list of the constraints in which the connector participates.
(define (make-connector)
(let ((value false) (informant false) (constraints '()))
(define (set-my-value newval setter)
(cond ((not (has-value? me))
(set! value newval)
(set! informant setter)
(for-each-except setter
inform-about-value
constraints))
((not (= value newval))
(error "Contradiction" (list value newval)))
(else 'ignored)))
(define (forget-my-value retractor)
(if (eq? retractor informant)
(begin (set! informant false)
(for-each-except retractor
inform-about-no-value
constraints))
'ignored))
(define (connect new-constraint)
(if (not (memq new-constraint constraints))
(set! constraints
(cons new-constraint constraints)))
(if (has-value? me)
(inform-about-value new-constraint))
'done)
(define (me request)
(cond ((eq? request 'has-value?)
(if informant true false))
((eq? request 'value) value)
((eq? request 'set-value!) set-my-value)
((eq? request 'forget) forget-my-value)
((eq? request 'connect) connect)
(else (error "Unknown operation: CONNECTOR" request))))
me))
(define (for-each-except exception procedure list)
(define (loop items)
(cond ((null? items) 'done)
((eq? (car items) exception) (loop (cdr items)))
(else (procedure (car items))
(loop (cdr items)))))
(loop list))
(define (has-value? connector) (connector 'has-value?)) (define (get-value connector) (connector 'value)) (define (set-value! connector new-value informant) ((connector 'set-value!) new-value informant)) (define (forget-value! connector retractor) ((connector 'forget) retractor)) (define (connect connector new-constraint) ((connector 'connect) new-constraint))
https://github.com/leicj/learning-SICP/blob/master/chapter3/3.33_1
3.4 Concurrency:Time Is of the Essence
The central issue lurking beneath the complexity of state, sameness, and change is that by introducing assignment we are forced to admit time into our computational models.Before we introduced assignment, all our programs were timeless, in the sense that any expression that has a value always has the same value.but think:
(withdraw 25) 75 (withdraw 25) 50
3.4.1 The Nature of Time in Concurrent Systems
let's talk about the withdraw process:
(define (withdraw amount)
(if (>= balance amount)
(begin
(set! balance (- balance amount))
balance)
"Insufficient funds"))
(set! balance (- balance amount))
Correct behavior of concurrent programs
The root of this complexity lies in the assignments to variables that are shared among the different processes.We already know that we must be careful in writing programs that use set!, because the results of a computation depend on the order in which the assignments occur.With concurrent processes we must be especially careful about assignments, because we may not be able to control the order of the assignments made by the different processes.If several such changes might be made concurrently we need some way to ensure that our system behaves correctly.
One possible restriction on concurrency would stipulate that no two operations that change any shared state variables can occur at the same time.
A less stringent restriction on concurrency would ensure that a concurrent system produces the same result as if the processes had run sequentially in some order.
There are still weaker requirements for correct execution of concurrent programs.A program for simulating diffusion might consist of a large number of processes, each one representing a small volume of space, that update their values concurrently.Each process repeatedly changes its value to the average of its own value and its neighbors' values.
3.4.2 Mechanisms for Controlling Concurrency
We've seen that the difficulty in dealing with concurrent processes is rooted in the need to consider the interleaving of the order of events in the different processes.For example, suppose we have two processes, one with three ordered events (a,b,c) and one with three ordered events (x,y,z).If the two processes run concurrently, with no constraints on how their execution is interleaved, then there are 20 different possible orderings for the vents that are consistent with the individual orderings for the two processes:
Serializing access to shared state
Serialization implements the following idea:Processes will execute concurrently, but there will be certain collections of procedures that cannot be executed concurrently.More precisely, serialization creates distinguished sets of procedures such that only one execution of a procedure in each serialized set is permitted to happen at a time.If some procedure in the set is being executed, then a process that attempts to execute any procedure in the set will be forced to wait until the first execution has finished.
Serializers in Scheme
Suppose that we have extended Scheme to include a procedure called parallel-execute:
(parallel-execute <p1> <p2> ... <pk>)
As an example of how this is used, consider:
(define x 10) (parallel-execute (lambda () (set! x (* x x))) (lambda () (set! x (+ x 1))))
but we could use (make-serializer) to make sure that process will be serialized.
(define x 10) (define s (make-serializer)) (parallel-execute (s lambda () (set! x (* x x))) (s lambda () (set! x (+ x 1))))
Here is a version of the make-account procedure, where deposits and withdrawals have been serialized:
(define (make-account balance)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(let ((protected (make-serializer)))
(define (dispatch m)
(cond ((eq? m 'withdraw) (protected withdraw))
((eq? m 'deposit) (protected deposit))
((eq? m 'balance) balance)
(else (error "Unknown request:MAKE-ACCOUNT"
m))))
dispatch))
Complexity of using multiple shared resources
While using serializers is relatively straightforward when there is only a single shared resource(such as a single bank account), concurrent programming can be treacherously difficult when where are multiple shared resources.
just think we wish to swap the balances in two bank accounts:
(define (exchange account1 account2)
(let ((difference (- (account1 'balance)
(account2 'balance))))
((account1 'withdraw) difference)
((account2 'deposit) difference)))
Peter might compute the difference in the balance for a1 and a2, but then Paul might change the balance in a1 before Peter is able to complete the exchange.It will be error.
One way we can accomplish this is by using both accounts' serializers to serialize the entire exchange procedure.To do this, we will arrange for access to an account's serializer.
(define (make-account-and-serializer balance)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(let ((balance-serializer (make-serializer)))
(define (dispatch m)
(cond ((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
((eq? m 'balance) balance)
((eq? m 'serializer) balance-serializer)
(else (error "Unknown request: MAKE-ACCOUNT" m))))
dispatch))
(define (deposit account amount)
(let ((s (account 'serializer))
(d (account 'deposit)))
((s d) amount)))
(define (serialized-exchange account1 account2)
(let ((serializer1 (account1 'serializer))
(serializer2 (account2 'serializer)))
((serializer1 (serializer2 exchange))
account1
account2)))
We implement serializers in terms of a more primitive synchronization mechanism called a mutex. A mutex is an object that supports two operations-the mutex can be acquired, and the mutex can be released.Once a mutex has been acquired, no other acquire operations on that mutex may proceed until the mutex is released.In our implementation, each serializer has an associated mutex.Given a procedure p, the serializer returns a procedure that acquires the mutex, runs p, and then releases the mutex.This ensures that only one of the procedures produced by the serializer can be running at once, which is precisely the serialization property that we need to guarantee.
(define (make-serializer)
(let ((mutex (make-mutex)))
(lambda (p)
(define (serialized-p . args)
(mutex 'acquire)
(let ((val (apply p args)))
(mutex 'release)
val))
serialized-p)))
(define (make-mutex)
(let ((cell (list false)))
(define (the-mutex m)
(cond ((eq? m 'acquire)
(if (test-and-set! cell)
(the-mutex 'acquire)));retry
((eq? m 'release) (clear! cell))))
the-mutex))
(define (clear! cell) (set-car! cell false))
(define (test-and-set! cell) (if (car cell) true (begin (set-car! cell true) false)))
Deadlock
two process, A and B. Peter run A and Paul run B, but Peter want to run B and Paul want to run A now. so A is waiting for B to release, and B is waiting for A to release.
this is the Deadlock.
3.5 Streams