【算法与数据结构】图 -- 十字链表

 

图的【十字链表】表示法是一种链式存储结构，可以看成是【邻接表】和【逆邻接表】的组合

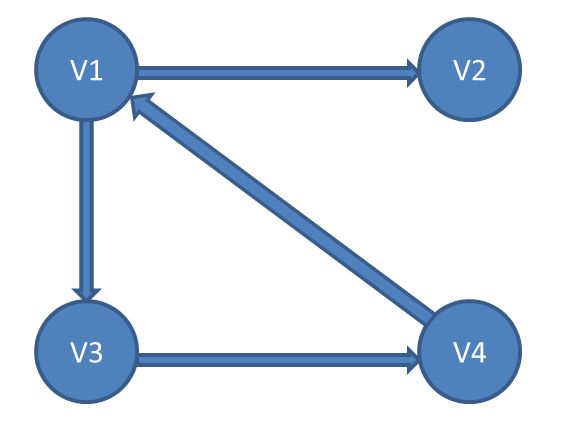
本文中用到的有向图

 

 

 

/************************************************************************ 有向图的存储：十字链表 有向图的十字链表存储结构，是有一种链式存储结构，可以看成是【邻接表】和【逆邻接表】 的结合。 图中每条弧对应一个【弧结点】，每个顶点对应一个【顶点结点】 弧结点 -------------------------------------------- | tailvex | headvex | hlink | tlink | info | -------------------------------------------- talivex:以该弧为【弧尾】的结点在图中的位置 headvex:以该弧为【弧头】的结点在图中的位置 hlink: 下一条与该弧有【相同弧头的弧】 tlink: 下一条与该弧有【相同弧尾的弧】 info: 弧的相关信息，权值等 顶点结点 ----------------------------- | data | firstin | firstout | ----------------------------- data: 该结点的数据 firstin: 第一条以该弧为弧头的【弧结点】 firstout:第一条以该弧为弧尾的【弧结点】 ************************************************************************/

 

 

 

相关数据结构

//顶点结点最大数量
int const MAX_VERTEXNUM = 100; //数据结构
 typedef int InfoType; typedef int Data; //弧结点
typedef struct _tagArcBox { int tailvex;              //该弧的弧尾结点在图中的位置
    int headvex;              //该弧的弧头结点在图中的位置
    struct _tagArcBox* hlink; //下一条与该弧有相同弧头结点的弧
    struct _tagArcBox* tlink; //下一条与该弧有相同弧尾结点的弧
    InfoType info;            //弧的相关信息
}ArcBox; //顶点结点
typedef struct _tagArcNode { Data data; //数据
    ArcBox* firstin;   //第一条以该节点为弧尾的弧
    ArcBox* firstout;  //第一条以该结点为弧头的弧
}ArcNode; //十字链表存储结构的有向图
typedef struct _tagOLGraph { ArcNode vertex[MAX_VERTEXNUM]; //顶点向量 

    int vexnum;       //顶点数
    int arcnum;       //弧树 
 }OLGraph, *POLGraph;

 

 

 

从顶点向量中查找该顶点在图中的位置(下标)

//输入图的【顶点向量】和某个顶点的数据 //获取此顶点在顶点向量中的位置(下标)
int LocateNode(ArcNode* pNodesArr, Data data, int length) { if( NULL == pNodesArr ) return NULL; for (int i = 0; i < length; ++ i) { if (pNodesArr[i].data == data) return i; } return -1; } //输入【图】和某顶点的数据 //获取该顶点在顶点向量中的位置(下标）
int LocateNode(POLGraph& pOLGraph, Data data) { return (NULL == pOLGraph ? NULL : LocateNode(pOLGraph->vertex, data, pOLGraph->vexnum) ); }

 

 

有向图的创建

/************************************************************************ 当使用这种函数原型时： void CreateOLGraph(POLGPraph& pOLGraph) { pOLGraph = new OLGraph(); //codes pOLGraph->vexnum = num; //这里报运行时错误！ why? } ************************************************************************/
//创建十字链表有向图 
POLGraph CreateOLGraph() { POLGraph pOlGraph = NULL; __try { pOlGraph = new OLGraph(); if(NULL == pOlGraph) {cerr << "申请图结点失败!\n"; return NULL;} int num = 0; cout << "请输入图的顶点数量:"; cin >> num; pOlGraph->vexnum = num; cout << endl; cout << "请输入图的弧的数量:"; cin >> num; pOlGraph->arcnum = num; cout << endl; Data data = 0; cout << endl << "--------开始 初始化顶点向量-----------"<<endl; for (int i = 0; i < pOlGraph->vexnum; ++i) { cout << "请输入结点的值:"; cin >> data; pOlGraph->vertex[i].data = data; pOlGraph->vertex[i].firstin = NULL; pOlGraph->vertex[i].firstout = NULL; cout<<endl; } //for
        cout <<endl<<"------------结束 初始化顶点向量------------"<<endl; cout<<endl<<endl; cout << "************开始 初始化弧结点 **************"<<endl; for(int i = 0; i < pOlGraph->arcnum; ++ i) { cout << "请输入弧的弧尾结点:"; cin >> data; int begin = LocateNode(pOlGraph->vertex, data, pOlGraph->arcnum); if(-1 == begin) {cerr << "您输入的弧尾结点不在图中，请重新输入"<<endl; --i; continue;} cout << "请输入弧的弧头结点:"; cin >> data; int end = LocateNode(pOlGraph->vertex, data, pOlGraph->arcnum); if(-1 == end) {cerr << "您输入的弧头结点不在图中，请重新输入"<<endl; -- i; continue;} cout << "请输入弧的权值:"; cin >> data; cout<<endl<<endl; ArcBox* pArcBox = new ArcBox(); if(NULL == pArcBox) {cerr << "申请弧结点失败!"<<endl; -- i; continue;} pArcBox->tailvex = begin;                           //该弧的弧尾在图中的位置
            pArcBox->headvex = end;                             //该弧的弧头在图中的位置
            pArcBox->hlink = pOlGraph->vertex[end].firstin;     //下一条与该弧有相同弧尾的弧结点
            pArcBox->tlink = pOlGraph->vertex[begin].firstout;  //下一条与该弧有相同弧头的弧结点
            pArcBox->info = data;                               //权值
 pOlGraph->vertex[begin].firstout = pOlGraph->vertex[end].firstin = pArcBox; } //for
 } //__try
 __except(1) { cerr << endl<<"有异常发生"<<endl; } return pOlGraph; }

 

 

运行情况：

 

 

 

 

出度和入度 

//求图的出度 //先根据输入的顶点的值，求得该点所在的顶点向量的分量 //然后得到该点的firstout，然后再得到所有与该弧有相同弧尾 //结点的弧(的条数)
int OutDegree(POLGraph& pOLGraph, Data data) { int nCount = 0; //根据结点的值定位该点在图的顶点向量中的位置（下标）
    int nIndex = LocateNode(pOLGraph, data); if(-1 == nIndex) {cerr << "该点不在图中，所以没有出度!\n"<<endl; return -1;} //得到该结点指针
    ArcNode* pArcNode = &(pOLGraph->vertex[nIndex]); if(NULL == pArcNode) {cerr << "在图中查找该顶点出错!\n"<<endl; return -1;} //第一条该顶点为弧尾的弧(该顶点结点的第一条出边)
    ArcBox* pArcBox = pArcNode->firstout; //查找所有以该【顶点结点】为【弧尾】的【弧结点】
    while(NULL != pArcBox) { ++ nCount; pArcBox = pArcBox->tlink; } return nCount; } //定点的入度
int InDegree(POLGraph& pOLGraph, Data data) { int nCount = 0; //定位该顶点结点在顶点向量中的位置（下标）
    int nIndex = LocateNode(pOLGraph, data); if(-1 == nIndex){cerr << "该点不在图中，所以没有入度!\n"<<endl; return -1;} //得到该顶点结点的指针
    ArcNode* pArcNode = &(pOLGraph->vertex[nIndex]); if(NULL == pArcNode) {cerr << "在图中查找该点出错!"<<endl; return -1;} //第一条以该顶点结点为弧头的弧(该顶点结点的第一条入边)
    ArcBox* pArcBox = pArcNode->firstin; //查找所有以该【顶点结点】为【弧头】的【弧结点】
    while(NULL != pArcBox) { ++nCount; pArcBox = pArcBox->hlink; } return nCount; }

 

 

 查找出度 / 入度

    POLGraph pGraph = CreateOLGraph(); int num = 0; for(int i = 0; i < pGraph->vexnum + 3; ++ i) { cout << "请输入带查的顶点的值:"; cin >> num; cout<<"结点 "<< num << " 的出度OutDegree为:"<<OutDegree(pGraph, num); cout<<endl; cout<<"结点 "<< num << " 的入度InDegree为:"<<InDegree(pGraph, num); cout<<endl<<endl; }

 

 

 

 

 

 

 

 深度优先遍历(DFS)  

/************************************************************************ 深度优先遍历 从某顶点出发，访问之，然后获得该顶点的第一条出边(firstout)，如果该出边 不为空，则获得该条出边的【弧头】结点在图中的位置(下标)，查看此下标的结点 是否被访问过，如果没有则根据此下标获取该结点，然后递归访问之；如果此结点 被访问过了，则说明出现回路，及此条弧指向了之前访问过的结点，需要跳出循环, 否则出现死循环。 ************************************************************************/

//顶点结点是否遍历过标志数组
bool* pVisited = NULL; void DFS(POLGraph& pOLGraph, ArcNode* pArcNode) { int nIndex = LocateNode(pOLGraph, pArcNode->data); pVisited[nIndex] = true; cout << "the node is "<<pArcNode->data<<endl; ArcBox* pArcBox = pArcNode->firstout; while(NULL != pArcBox) { //该弧的弧头在图中的位置
        int nHeadVex = pArcBox->headvex; if (pVisited[nHeadVex] == false) { ArcNode* pHeadNode = &(pOLGraph->vertex[nHeadVex]); DFS(pOLGraph, pHeadNode); } //如果某条弧的弧头结点已经被访问过时，则说明已经有了回路，此时要跳出循环 //否则会在while中死循环
        else { break; } } } //有向图的深度优先遍历
void DFSTraverse(POLGraph& pOLGraph) { if(NULL == pOLGraph) {cerr << "该图为空!"; return;} pVisited = new bool[pOLGraph->vexnum](); for (int i = 0; i < pOLGraph->vexnum; ++ i) pVisited[i] = false; for (int i = 0; i < pOLGraph->vexnum; ++ i) { if (! pVisited[i]) { DFS(pOLGraph, &pOLGraph->vertex[i]); } } }

 

 

深度优先遍历结果 

 

 

 

 

 

 

 

 

广度优先遍历(BFS)

 关于广度优先遍历，我见到两种写法

这两种写法大致如下

 

方式1

for(int i = 0; i < 图中点的数量; ++ i) { if(结点 i 没有被访问过) { 访问之 入队 while(队不空) { 出队 访问队头结点所有邻接点，将访问过的邻接点的访问标志数组的分量 置为true; } 将该结点 i 置为邻接点访问过 } } 

 

 

 

 

方式2

int nStart = 0;  //从图中位置为nStart的结点开始遍历
将该结点入队 访问该nStart结点 if(nStart结点的邻接点没有被访问) { while(队不空) { 队头元素出队 while(队头元素仍然有出边) { 访问队头元素的所有出边的弧头结点，并置访问过的结点的 访问标志置为true } } //while
 将该点的 邻接点访问标志 置为true } //if
 

 

 

 

 

 

 下面是这两种方式的代码实现，图的存储结构是十字链表（有向图的存储结构）

 

//----------------------------方式1------------------------------------ //有向图的广度优先遍历 
 
void BFS(POLGraph& pOLGraph) { if(NULL == pOLGraph) return; bool *pVisitedLinjie = new bool[pOLGraph->vexnum]; pVisited = new bool[pOLGraph->vexnum]; for(int i = 0; i < pOLGraph->vexnum; ++ i){pVisited[i] = false; pVisitedLinjie[i] = false;} queue<ArcNode*> quArcNode; for (int i = 0; i < pOLGraph->vexnum; ++ i) { if (pVisited[i] == false) { cout << "data of node is "<<pOLGraph->vertex[i].data<<endl; quArcNode.push(&(pOLGraph->vertex[i])); while(! quArcNode.empty()) { //取队头元素， 并出队
                ArcNode* pArcNode = quArcNode.front(); quArcNode.pop(); //定位该队头元素在图中的位置
                int nIndex = LocateNode(pOLGraph, pArcNode->data); if(-1 == nIndex) return; //如果该结点的【邻接点】【未被访问】
                if (pVisitedLinjie[nIndex] == false) { //访问其所有邻接点 //找队头元素的第一条【出边】
                    ArcBox* pArcBox = pArcNode->firstout; while(NULL != pArcBox) { //定位该弧的【弧头结点】在图中的位置
                        int nHead = pArcBox->headvex; //如果该弧头节点【未被访问】，则访问之，如果已被访问则说明出现了环
                        if (false == pVisited[nHead]) { cout << "data of node is "<<pOLGraph->vertex[nHead].data<<endl; //将该弧头节点置为【访问过】
                            pVisited[nHead] = true; //将该结点 入队
                            quArcNode.push(&(pOLGraph->vertex[nHead])); //下一条与该弧有相同【弧尾】的弧
                            pArcBox = pArcBox->tlink; } else { //出现了环，退出
                            break; } } //到这，该节点的所有邻接点都访问过了 //将其邻接点访问标记 标为【访问过】 
                    pVisitedLinjie[nIndex] = true; } //if 
 } //while
 } } }

 

 

 

 

 

 

//------------------------------方式2------------------------------------ //nStart为从图中位置为nStart的结点开始遍历
void BFS(POLGraph& pOLGraph, int nStart) { if(NULL == pOLGraph) return; bool *pVisitedLinjie = new bool[pOLGraph->vexnum]; pVisited = new bool[pOLGraph->vexnum]; for(int i = 0; i < pOLGraph->vexnum; ++ i){pVisited[i] = false; pVisitedLinjie[i] = false;} cout << "data of node is "<<pOLGraph->vertex[nStart].data<<endl; pVisited[nStart] = true; queue<ArcNode*> quArcNode; quArcNode.push(&(pOLGraph->vertex[nStart])); if (pVisited[nStart] == false) { cout << "data of node is "<<pOLGraph->vertex[i].data<<endl; quArcNode.push(&(pOLGraph->vertex[i])); while(! quArcNode.empty()) { //取队头元素， 并出队
            ArcNode* pArcNode = quArcNode.front(); quArcNode.pop(); //定位该队头元素在图中的位置
            int nIndex = LocateNode(pOLGraph, pArcNode->data); if(-1 == nIndex) return; //如果该结点的【邻接点】【未被访问】
            if (pVisitedLinjie[nIndex] == false) { //访问其所有邻接点 //找队头元素的第一条【出边】
                ArcBox* pArcBox = pArcNode->firstout; while(NULL != pArcBox) { //定位该弧的【弧头结点】在图中的位置
                    int nHead = pArcBox->headvex; //如果该弧头节点【未被访问】，则访问之，如果已被访问则说明出现了环
                    if (false == pVisited[nHead]) { cout << "data of node is "<<pOLGraph->vertex[nHead].data<<endl; //将该弧头节点置为【访问过】
                        pVisited[nHead] = true; //将该结点 入队
                        quArcNode.push(&(pOLGraph->vertex[nHead])); //下一条与该弧有相同【弧尾】的弧
                        pArcBox = pArcBox->tlink; } else { //出现了环，退出
                        break; } } //到这，该节点的所有邻接点都访问过了 //将其邻接点访问标记 标为【访问过】 
                pVisitedLinjie[nIndex] = true; } //if 
 } //while
    } //if
 }