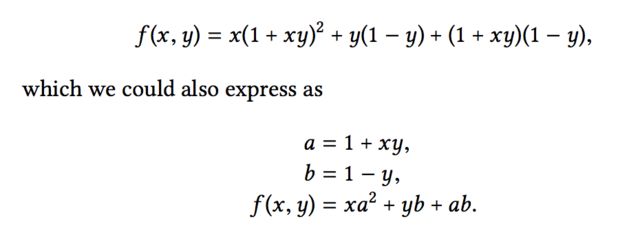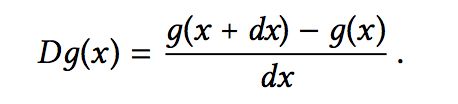SICP:Building Abstractions with Procedures
1.1 The Elements of Programming
1.1.1 Expressions
advantage of prefix notation:
1. take an arbitrary number of argument
> (+ 21 34 12 7) 742. it extends in a straight forward way to allow combinations to be nested
> (+ (* 3 5) (- 10 6)) 19
1.1.2 Naming and the Environment
we use define to name things:
> (define radius 10) > (* pi (* radius radius)) 314.1592653589793 > (define circumference (* 2 pi radius)) > circumference 62.83185307179586
1.1.3 Evaluating Combinations
evaluating combinations by two steps:
1. Evaluate the subexpressions of the combination.
2. Apply the procedure that is the value of the leftmost subexpression(the operator) to the arguments that the values of the other subexpressions(the operands)
1.1.4 Compound Procedures
powerful elements:
1. Numbers and arithmetic operations are primitive data and procedures.
2. Nesting of combinations provides a means of combining operations.
3. Definitions that associate names with values provide a limited means of abstraction.
The general form of a procedure definition is:
(define (<name> <formal parameters>) <body>)the good example is:
(define (square x) (* x x)) (define (sum-of-squares x y) (+ (square x) (square y))) ;25 (sum-of-squares 3 4)
1.1.5 The Substitution Model for Procedure Application
The application process is as follows:
To apply a compound procedure to arguments, evaluate the body of the procedure with each formal parameter replaced by the corresponding argument.
so, (sum-of-squares 3 4) first to be:
(sum-of-squares 3 4) -> (+ (square 3) (square 4)) -> (+ (* 3 3) (* 4 4)) -> (+ 9 16) -> 25The process we have just described is called the substitution model, also called applicative-order evaluation.
but there has another evaluation: normal-order evaluation.
(define (square x) (* x x)) (define (sum-of-squares x y) (+ (square x) (square y))) (define (f a) (sum-of-squares (+ a 1) (* a 2))) ;normal-order evaluation (sum-of-squares (+ 5 1) (* 5 2)) -> (+ (square (+ 5 1)) (square (* 5 2))) -> (+ (* (+ 5 1) (+ 5 1)) (* (* 5 2) (* 5 2))) -> (+ (* 6 6) (* 10 10)) -> (+ 36 100) -> 136 ;applicative-order evaluation (sum-of-squares (+ 5 1) (* 5 2)) -> (+ (square 6) (square 10)) -> (+ (* 6 6) (* 10 10)) -> (+ 36 100) -> 136LISP use applicative-order evaluation.
1.1.6 Conditional Expressions and Predicates
conditional expression is:
(cond (<p1> <e1>)
(<p2> <e2>)
...
(<pn> <en>))
(cond (<p1> <e1>
(<p2> <e2>)
...
(<pn> <en>)
(else <e>)))
(if <predicate> <consequent> <alternative>) if we want to accumulate the abs,we could write:
(define (abs x)
(cond ((> x 0) x)
((= x 0) 0)
((< x 0) (- x))))
;better use else
(define (abs x)
(cond ((< x 0) (- x))
(else
x)))
;also use if
(define (abs x)
(if (< x 0)
(- x)
x)) we could use “and”, “or”, “not” to judge the condition.
1.1.7 Example:Square Roots by Newton’s Method
how could we accumulate the square-root:
we could use Newton’s method of successive approximations, which says that whenever we have a guess y for the value of the square root of a number x, we can perform a simple manipulation to get a better guess(one closer to the actual square root) by averaging y with x/y. For example:
we could write LISP code:
(define (sqrt-iter guess x)
(if (good-enough? guess x)
guess
(sqrt-iter (improve guess x) x)))
(define (improve guess x)
(average guess (/ x guess)))
(define (average x y)
(/ (+ x y) 2))
(define (good-enough? guess x)
(< (abs (- (square guess) x)) 0.001))
(define (square x) (* x x))
(define (new-sqrt x)
(sqrt-iter 1.0 x))
;3.00009155413138
(new-sqrt 9)
;11.704699917758145
(new-sqrt 137)
1.1.8 Procedures as Black-Box Abstractions
Local names:
A formal parameter of a procedure has a very special role in the procedure definition, in that it doesn’t matter what name the formal parameter has. Such a name in called a bound variable, and we say that the procedure definition binds its formal parameters. The meaning of a procedure definition is unchanged if a bound variable is consistently renamed throughout the definition. If a variable is not bound, we say that it is free. The set of expressions for which a binding defines a name is called the scope of that name. In a procedure definition, the bound variables declared as the formal parameters of the procedure have the body of the procedure as their scope.
Internal definitions and block structure:
the sqrt function has a problem that: like good-enough?, improve and sqrt-iter function, it only be using for sqrt, not for others. so we could define them in internal:
(define (new-sqrt x)
(define (square x) (* x x))
(define (good-enough? guess x)
(< (abs (- (square guess) x)) 0.001))
(define (average x y)
(/ (+ x y) 2))
(define (improve guess x)
(average guess (/ x guess)))
(define (sqrt-iter guess x)
(if (good-enough? guess x)
guess
(sqrt-iter (improve guess x) x)))
(sqrt-iter 1.0 x))
;3.00009155413138
(new-sqrt 9)
;11.704699917758145
(new-sqrt 137)
this call block structure.
because the x will not be changed, we also write like that:
(define (new-sqrt x)
(define (square x) (* x x))
(define (good-enough? guess)
(< (abs (- (square guess) x)) 0.001))
(define (average x y)
(/ (+ x y) 2))
(define (improve guess)
(average guess (/ x guess)))
(define (sqrt-iter guess)
(if (good-enough? guess)
guess
(sqrt-iter (improve guess))))
(sqrt-iter 1.0))
;3.00009155413138
(new-sqrt 9)
;11.704699917758145
(new-sqrt 137)
1.2 Procedures and the Processes They Generate
1.2.1 Linear Recursion and Iteration
when we considering the factorial function:
n! = n · (n − 1) · (n − 2) · · · 3 · 2 · 1.we have two method. one is recursion, we could write like that:
n! = n · [(n − 1) · (n − 2) · · · 3 · 2 · 1] = n · (n − 1)!so the lisp code like that:
(define (factorial n)
(if (= n 1)
1
(* n (factorial (- n 1)))))
;120
(factorial 5) and we could use
iteration.
(define (factorial n)
(define (iter-factorial product counter)
(if (> counter n)
product
(iter-factorial (* product counter)
(+ counter 1))))
(iter-factorial 1 1))
;120
(factorial 5)
now we discuss the two process.the first process using deferred operations:
recursive process.
Carrying out this process requires that the interpreter keep track of the operations to be performed later on. because it keep n track, so we called the process a linear recursive process.
but the second process doesn’t keep track,
every step accumulate the result, so we called this an
iterative process.In general, an iterative process is one whose state can be summarized by a fixed number of state variables, together with a fixed rule that describes
how the state variables should be updated as the process moves from state to state and an (optional) end test that specifies conditions under which the process should terminate.
1.2.2 Tree Recursion
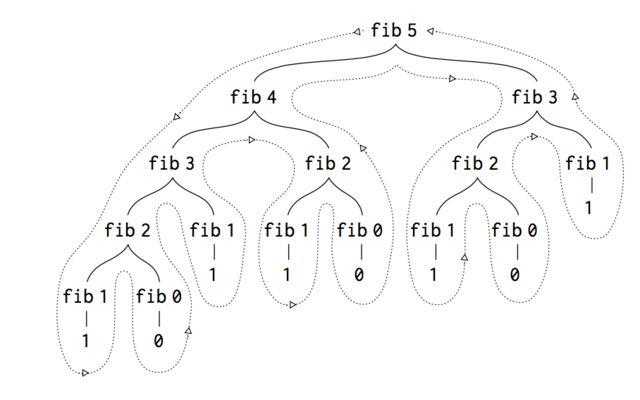
we could write the Fibonacci:
then we write the lisp code:
(define (fib n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 1))
(fib (- n 2))))))
;55
(fib 10)
it’s a tree recursion, like that:
we could also write it in iteration:
(define (fib-recursive n)
(define (iter-fib a b count)
(if (= count n)
a
(iter-fib b (+ a b) (+ count 1))))
(iter-fib 0 1 0))
;55
(fib-recursive 10)
Example: Counting change
just think we have $1.00, how many method could we have to make $1.00 into 50, 25, 10, 5, 1 pennies?
The number of ways to change amount a($1.00) using n(5 : 50, 4 : 25, 3 : 10, 2 : 5, 1 : 1) kinds of coins equals:
1. the number of ways to change amount
a but the first kind of coin, plus
2. the number of ways to change amount a - d using all n kinds of coins, where d is the denomination of the first kind of coin.
the code:
(define (count-change amount) (cc amount 5))
(define (cc amount kinds-of-coins)
(cond
;amount == 0,1 method
((= amount 0) 1)
((or (< amount 0) (= kinds-of-coins 0)) 0)
(else (+
;the number of ways to change amount using all but the
;first kind of coin(kinds-of-coins - 1)
(cc amount (- kinds-of-coins 1))
;the number of ways to change amount - the value of kinds-of-coins
(cc (- amount (first-denomination kinds-of-coins)) kinds-of-coins)))))
(define (first-denomination kinds-of-coins)
(cond ((= kinds-of-coins 1) 1)
((= kinds-of-coins 2) 5)
((= kinds-of-coins 3) 10)
((= kinds-of-coins 4) 25)
((= kinds-of-coins 5) 50)))
;292
(count-change 100)
1.2.3 Orders of Growth
we use the
R(n) = Θ(f (n))
to indicate the orders of growth, when the:
k1 f (n) ≤ R(n) ≤ k2 f (n)
we also know that n^2 == 1000n^2 == 3n^2 + 10n + 17 for the R(n).
the solution for 1.15:
the question is: when x is small, sin x == x. so we accumulate the sin x = 3sin(x / 3) - 4sin^3(x / 3):
(define (cube x) (* x x x))
(define (p x) (- (* 3 x) (* 4 (cube x))))
(define (sine angle)
(if (not (> (abs angle) 0.1))
angle
(p (sine (/ angle 3.0)))))
(sine 12.15)
-> (p (sine 405 / 100))
-> (p (p (sine 135 / 100)))
-> (p (p (p (sine 45 / 100))))
-> (p (p (p (p (sine 15 / 100)))))
-> (p (p (p (p (p (sine 5 / 100))))))
-> (p (p (p (p (p 0.05)))))
so we accumulate five times.
we find the (p (p (p (p (p 0.05))))) is a tree, so the R(n) = log(n).
1.2.4 Exponentiation
when we accumulate the b^n, we have two method: the recursive and the iteration:(define (expt-recursive b n)
(if (= n 0)
1
(* b (expt-recursive b (- n 1)))))
(define (expt-iteractive b n)
(define (iter-expt index product)
(if (= index n)
product
(iter-expt (+ index 1) (* product b))))
(iter-expt 1 b))
;1024
(expt-recursive 2 10)
;1024
(expt-iteractive 2 10)
but there have a good method like that:
bn = (b^n/2)2 if n is even,
bn =b·b^(n−1) if n is odd.
so we could write the code:
(define (square x) (* x x))
(define (fast-expt b n)
(cond ((= n 0) 1)
((even? n) (square (fast-expt b (/ n 2))))
(else
(* b (fast-expt b (- n 1))))))
;1024
(fast-expt 2 10)
1.2.5 Greatest Common Divisors
when we accumulate the greatest common divisor of two integers a and b, we have one method:
GCD(a, b) = GCD(b, r), r = a % b. so the code like that:
(define (gcd-recursive a b)
(if (= b 0)
a
(gcd-recursive b (remainder a b))))
;4
(gcd-recursive 204 40)
1.2.6 Example: Testing for Primality
Searching for divisors
we could use the stupid method to find the prime:
(define (smallest-divisor n) (find-divisor n 2))
(define (find-divisor n test-divisor)
(cond ((> (square test-divisor) n) n)
((divides? test-divisor n) test-divisor)
(else
(find-divisor n (+ test-divisor 1)))))
(define (divides? a b) (= (remainder b a) 0))
(define (square x) (* x x))
(define (prime? n)
(= n (smallest-divisor n)))
;#t
(prime? 101)
;#f
(prime? 99)
The Fermat test
Fermat’s Little Theorem: If n is a prime number and a is any positive integer less than n, then a raised to the nth power is congruent to a modulo n.
if n is not prime, then most of the numbers a < n will not satisfy the above relation. so if a satisfy the
Fermat’s Little Theorem, that n is could be a prime, then we choose another value a to check, this call
the Fermat test.
(define (square x) (* x x))
(define (expmod base exp m)
(cond ((= exp 0) 1)
((even? exp)
(remainder
(square (expmod base (/ exp 2) m))
m))
(else
(remainder
(* base (expmod base (- exp 1) m))
m))))
(define (fermat-test n)
(define (try-it a)
(= (expmod a n n) a))
(try-it (+ 1 (random (- n 1)))))
(define (fast-prime? n times)
(cond ((= times 0) true)
((fermat-test n) (fast-prime? n (- times 1)))
(else false)))
;#t
(fast-prime? 101 3)
;#f
(fast-prime? 99 3)
1.3 Formulating Abstractions with Higher-Order Procedures
1.3.1 Procedures as Arguments
consider the following three procedures:
(define (sum-integers a b)
(if (> a b)
0
(+ a (sum-integers (+ a 1) b))))
(define (sum-cubes a b)
(if (> a b)
0
(+ (cube a)
(sum-cubes (+ a 1) b))))
(define (pi-sum a b)
(if (> a b)
0
(+ (/ 1.0 (* a (+ a 2)))
(pi-sum (+ a 4) b)))) the three procedures have the same template:
(define (<name> a b)
(if (> a b)
0
(+ (<term> a)
(<name> (<next> a) b)))) there has a math concept:
so we now could write our code:
(define (sum term a next b)
(if (> a b)
0
(+ (term a)
(sum term (next a) next b))))
(define (inc n) (+ n 1))
(define (cube x) (* x x x))
(define (sum-cubes a b)
(sum cube a inc b))
;3025
(sum-cubes 1 10)
(define (sum-integers a b)
(sum identity a inc b))
;55
(sum-integers 1 10)
(define (pi-sum a b)
(define (pi-term x)
(/ 1.0 (* x (+ x 2))))
(define (pi-next x)
(+ x 4))
(sum pi-term a pi-next b))
;3.141392653591793
(* 8 (pi-sum 1 10000)) we could also write below method:
the code is:
(define (sum term a next b)
(if (> a b)
0
(+ (term a)
(sum term (next a) next b))))
(define (integral f a b dx)
(define (add-dx x)
(+ x dx))
(* (sum f (+ a (/ dx 2.0)) add-dx b) dx))
(define (cube x) (* x x x))
;0.24998750000000042
(integral cube 0 1 0.01)
;0.249999875000001
(integral cube 0 1 0.001)
1.3.2 Constructing Procedures Using lambda
lambda define that:
(lambda (<formal-paramters>) <body>)so:
(define (plus4 x) (+ x 4)) -> (define plus4 (lambda (x) (+ x 4)))Using let to create local variables
if we accumulate:
so we first must write like that:
(define (f x y)
(define (f-helper a b)
(+ (* x (square a b))
(* y b)
(* a b)))
(f-helper (+ 1 (* x y))
(- 1 y))) but we learn the lambda, we could write like that:
(define (f x y)
((lambda (a b)
(+ (* (square a))
(* y b)
(* a b)))
(+ 1 (* x y))
(- 1 y))) but the best method is to use let:
(define (f x y)
(let ((a (+ 1 (* x y)))
(b (- 1 y)))
(+ (* x (square a))
(* y b)
(* a b)))) let define that:
and it is a syntactic sugar for the lambda:
there has two way to notice the let:
1. let allows one to bind variables as locally as possible to where they are to be used. For example, if the value of x is 5, the value of the expression:
(+ (let ((x 3))
(+ x (* x 10)))
x)
is 38. the x in the body is 3, and out of the body is 5.
2. The variables’s values are computed outside the let. so if the value of x is 2, the expression:
(let ((x 3)
(y (+ x 2)))
(* x y)) will have the value 12 because, inside the body of the let, x will be 3, and y will be 4 = 2 + 2.
1.3.3 Procedures as General Methods
Finding roots of equations by the half-interval methodthe half-interval method use to find roots make f(x) = 0.
f(a) < 0 < f(b), that we make mid = (a + b) / 2.
if f(mid) > 0, we use f(a) < 0 < f(mid);
if f(mid) < 0, we use f(mid) < 0 < f(b).
if a and b is close enough or f(mid) = 0, we find the answer.
the LISP code is:
(define (average x y) (/ (+ x y) 2.0))
(define (search f neg-point pos-point)
(let ((midpoint (average neg-point pos-point)))
(if (close-enough? neg-point pos-point)
midpoint
(let ((test-value (f midpoint)))
(cond ((positive? test-value)
(search f neg-point midpoint))
((negative? test-value)
(search f midpoint pos-point))
(else midpoint))))))
(define (close-enough? x y) (< (abs (- x y)) 0.01))
(define (half-interval-method f a b)
(let ((a-value (f a))
(b-value (f b)))
(cond ((and (negative? a-value) (positive? b-value))
(search f a b))
((and (negative? b-value) (positive? a-value))
(search f b a))
(else
(error "Values are not of opposite sign" a b)))))
;3.14453125
(half-interval-method sin 2.0 4.0)
Finding fixed points of functions
A number x is called a
fixed point of a function f if x satisfies the equation f(x) = x. so we could: f(x), f(f(x)), f(f(f(x))), ...
until the value does not change very much.
(define tolerance 0.00001)
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs (- v1 v2))
tolerance))
(define (try guess)
(let ((next (f guess)))
(if (close-enough? guess next)
next
(try next))))
(try first-guess))
;0.7390822985224023
(fixed-point cos 1.0) when we accumulate y^2 = x, we could use y = x / y, and define the function:
(define (sqrt x)
(fixed-point (lambda (y) (/ x y))
1.0))
but it will be infinite loop. consider an initial guess y1, the next guess is y2 = x / y1, and the y3 = x / y2 = x / (x / y1) = y1, so the guess between y1 and y2.we should change like that:
y = 1/2(y + x / y). and the code like that:
(define tolerance 0.00001)
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs (- v1 v2))
tolerance))
(define (try guess)
(let ((next (f guess)))
(if (close-enough? guess next)
next
(try next))))
(try first-guess))
(define (average x y) (/ (+ x y) 2))
(define (sqrt-new x)
(fixed-point (lambda (y) (average y (/ x y)))
1.0))
;3.3166247903554
(sqrt-new 11)
1.3.4 Procedures as Returned Values
we use the average to accumulate the y = x ^ 2, we could also use:
(define (average-damp f) (lambda (x) (average x (f x))))
to accumulate too:
(define (sqrt x)
(fixed-point (average-damp (lambda (y) (/ x y)))
1.0))
Newton’s method
for the method:
when g(x) = 0, x->f(x). so that is why when g(x) = y^2 - x = 0, we could accumulate sqrt x.
but we first accumulate the Dg(x):
we could write the code:
(define (deriv g) (lambda (x) (/ (- (g (+ x dx)) (g x)) dx))) (define dx 0.00001)
(define (deriv g)
(lambda (x) (/ (- (g (+ x dx)) (g x)) dx)))
(define dx 0.00001)
(define (newton-transform g)
(lambda (x) (- x (/ (g x) ((deriv g) x)))))
(define (newtons-method g guess)
(fixed-point (newton-transform g) guess))
(define (square x) (* x x))
(define (sqrt-new x)
(newtons-method
(lambda (y) (- (square y) x)) 1.0))
(define tolerance 0.00001)
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs (- v1 v2))
tolerance))
(define (try guess)
(let ((next (f guess)))
(if (close-enough? guess next)
next
(try next))))
(try first-guess))
;3.316624790355423
(sqrt-new 11)