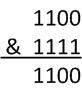Map实现之HashMap(性能及算法)
转载:http://286.iteye.com/blog/2189266
上一篇重点介绍的是HashMap的实现原理、设计思想与相关具体操作,本篇就深入HashMap实现中进一步了解其内部的一些算法及相关性能指标。
HashMap实例中table的length是在初始化时就被指定的,无论采用默认值还是其他指定值,table数组的大小就已经确定,随着添加元素的增多在一定时机下下会对table数组进行扩容呢。
HashMap实例通过put方法设置元素,HashMap实例首先会计算该key所对应的下标位置,然后遍历寻找该key,如果找到则直接更新,当该 key为原实例中不存在时则会调用addEntry方法添加新的元素,此时Map实例的size属性就会+1,并且进行扩容判断:
Java代码 ![]()
void addEntry(int hash, K key, V value, int bucketIndex) {
Entry<K, V> e = table[bucketIndex];
table[bucketIndex] = new Entry<K, V>(hash, key, value, e);
//进行判断,是否扩容
if (size++ >= threshold)
resize(2 * table.length);
}
其中 threshold=(int)(capacity * loadFactor);(数组长度*负载因子),当table默认长度为16时,threshold就为12,所以当size达到或超过12时就会调用 resize方法进行扩容。扩容后table长度变为原来的两倍。
以下是resize方法的源代码:
Java代码 ![]()
void resize(int newCapacity) {
Entry[] oldTable = table;
int oldCapacity = oldTable.length;
if (oldCapacity == MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return;
}
Entry[] newTable = new Entry[newCapacity];
transfer(newTable);
table = newTable;
threshold = (int) (newCapacity * loadFactor);
}
resize方法核心就是创建一个新的数组newTable,该数组大小为newCapacity(newCapacity=2 * table.length),也就是两倍于原数组大小。然后调用transfer(newTable)方法进行重新指向,通俗一点讲就是把table里面 的东西倒腾到newTable里。
transfer将原table中的Entry元素重新分配至新的newTable数组中,并且原table数组中的元素所在下标顺序可能发生变化,以下为transfer源代码:
Java代码 ![]()
/**
* 将table中所有Entry元素转移至newTable
*/
void transfer(Entry[] newTable) {
Entry[] src = table;
int newCapacity = newTable.length;
for (int j = 0; j < src.length; j++) {
Entry<K, V> e = src[j];
if (e != null) {
src[j] = null;
do {
Entry<K, V> next = e.next;
int i = indexFor(e.hash, newCapacity);
e.next = newTable[i];
newTable[i] = e;
e = next;
} while (e != null);
}
}
}
从源代码int i = indexFor(e.hash, newCapacity);可以看出,这里根据新数组长度重新计算了Entry元素插入的下标位置,所以在进行resize之后Entry所在下标位置可能发生变化,如图所示:

图示中Entry下标经过方法indexFor(int h, int length)进行了重新计算,所以结果下标是有可能变化的。
最后将table的引用指向了newTable,所以原table的数组实例就变为了垃圾,等待GC进行处理
总结:避免频繁出现这种操作是有必要的,这样既有利于合理利用内存空间,避免不必要的垃圾产生,又可以提高HashMap实例的性能,那么又该如何提高HashMap实例的性能呢?
HashMap实例性能
HashMap 实例有两个参数(上一篇的属性中介绍过)影响其性能:“初始容量”和“负载因子”。
容量(capacity):哈希表中容器的数量,初始容量只是哈希表在创建时的容量。
负载因子(load factor):哈希表在其容量自动增加之前可以达到多满的一种尺度。当哈希表中的条目数超出了负载因子与当前容量的乘积时,则要对该哈希表进行 rehash 操作(即重建内部数据结构),从而哈希表将具有大约两倍的容器数量。
可以说容量与负载因子的合理设置与否直接影响着HashMap的性能指标,我们在初始化时可以指定这两个参数:
Java代码 ![]()
//capacity=32,load factor=0.75
Map map=new HashMap<String,String>(32,0.75f);
此时HashMap会调用重载构造方法进行初始化,重载构造函数源代码如下:
Java代码 ![]()
/**
* 使用指定容量和负载因子构建一个空的HashMap实例
*/
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " + loadFactor);
// Find a power of 2 >= initialCapacity
int capacity = 1;
while (capacity < initialCapacity)
capacity <<= 1;
this.loadFactor = loadFactor;
threshold = (int) (capacity * loadFactor);
table = new Entry[capacity];
init();
}
重载构造方法会根据我们指定的容量与负载因子进行了初始化操作。
我们通过以下几个实验来探究下容量与负载因子对HashMap实例性能的影响:
1)实验一
实验原理:创建几个HashMap实例,初始化时指定不同的容量大小,并且它们采用默认相同的负载因子,向每个HashMap实例中添加1000000个元素,计算总用时,每个实验进行一定次数,得出对比分析图。
实验结果:
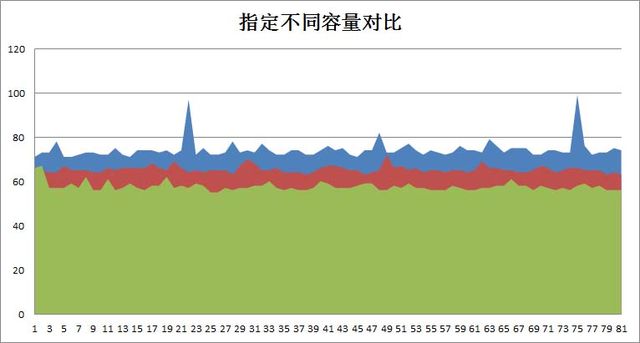 图中蓝色部分代表指定较小容量值;图中红色部分代表指定中等容量值;图中绿色部分代表指定合理容量值;
图中蓝色部分代表指定较小容量值;图中红色部分代表指定中等容量值;图中绿色部分代表指定合理容量值;
实验局限性:实验过程中会与使用机器硬件及相关参数设置是否合理有关,而且实验过程中可能会出现垃圾收集导致返回时间较长的情况,所以需要更大范围与更多次数的对比分析。但实验的结果方向性是正确的,可以作为参考。
实验结论:从实验结果可以很直观的看出,当我们指定的HashMap实例大小越接近实际使用大小,HashMap的性能越好。所以在加载因子不变的情况下,指定更合理的大小值可以有效的提高HashMap实例的性能。
2)实验二
实验原理:创建几个HashMap实例,初始化时指定相同的容量大小,不同的负载因子,向每个HashMap实例中添加1000000个元素,计算总用时,每个实验进行一定次数,得出对比分析图。
实验过程:
(1)默认长度为16,创建4个HashMap实例,它们的负载因子分别为0.25,0.5,0.75和1,代码如下:
Java代码 ![]()
Map map1 = new HashMap<String, String>(16,0.25f);
Map map2 = new HashMap<String, String>(16,0.5f);
Map map3 = new HashMap<String, String>(16,0.75f);
Map map4 = new HashMap<String, String>(16,1f);
(2)不断向几个实例中填充元素,得到实验结果:
图中几条曲线是指定初始化容量较小时,不同负载因子对实例性能的影响,从中可以看出负载因子为0.5时这个HashMap的实例性能最好。负载因子为1时性能最差。
(3)指定HashMap实例初始容量为1232896,创建4个HashMap实例,它们的负载因子分别为0.25,0.5,0.75和1,代码如下:
Java代码 ![]()
Map map1 = new HashMap<String, String>(1232896,0.25f);
Map map2 = new HashMap<String, String>(1232896,0.5f);
Map map3 = new HashMap<String, String>(1232896,0.75f);
Map map4 = new HashMap<String, String>(1232896,1f);
(4)不断向几个实例中填充元素,得到实验结果:
图中几条曲线是指定初始化容量较大时,不同负载因子对实例性能的影响,从中可以看出负载因子为0.25时这个HashMap的实例性能最差,其他负载因子的性能差不多。
实验结果:当添加元素较少时可以使用默认负载因子,此时性能差异并不明显;当添加元素较多时,可以通过测试或估算取得较佳的负载因子值。
实验局限性:实验过程中受添加元素数量的影响较大,元素数量级越大加载因子影响越大。
实验结论: 测试受多方面因素影响,添加不同数量元素的情况下相同的负载因子在性能影响上并不一致,只有根据实际运用情况来合理配置容量与负载因子的乘积才会使HashMap实例的性能更优,无法判断的情况下以默认值为最佳。
综合结论:为了提高HashMap实例的性能,我们可以在初始化时估算出要添加元素的数量,从 而指定足以容纳这些元素的HashMap容量数值,负载因子在元素个数不同的情况下对HashMap实例的影响较大,再未通过测试的情况下可以采用默认值 (未必是最优值),否则将降低实例的性能。
HashMap中的相关计算方法
在HashMap实现中有一些特定的方法,诸如计算下标,计算hash值等,这些方法被用于特定的场合,虽算不上比较复杂的算法,但重要性不可小看。
1.indexFor方法
indexFor(int h, int length)方法根据指定hash值和数组长度计算出该hash值所对应数组下标。indexFor在获取、添加元素等方法中担任重要角色。
以下是indexFor方法的源代码:
Java代码 ![]()
/**
* 根据hash值h与数组长度length计算下标位置
*/
static int indexFor(int h, int length) {
return h & (length - 1);
}
核心代码只有一行,但是却不要小看它。indexFor采用的是“按位与”的方式来计算出下标位置,“&”的操作其实就是将十进制的数转换成二进制后两个二进制数按相同位进行“与”计算,相同值“与”计算后结果不变,不同值“与”计算后结果为0.
注意:因为下标是从0开始的,以长度16为例,下标范围为0-15,所以代码中使用的是length-1
以length=16为例,计算hash值为12,15,46,90的index值
几个hash值对应二进制表示为:
| 十进制hash值 | 二进制值 |
| 12 | 1100 |
| 15 | 1111 |
| 90 | 1011010 |
| 234 | 11101010 |
此时h & (length - 1)结果即为(以hash为12为例):
12 & 15:
类似的其他结果如下:
| 十进制hash值 | 二进制值 | 计算结果 |
| 12 | 1100 | 12 |
| 15 | 1111 | 15 |
| 90 | 1011010 | 10 |
| 234 | 11101010 | 10 |
总结:indexFor方法采用“&”操作最大的优点就是在计算出下标位置的同时又注重了高效率。
2.hash方法
HashMap为什么要单独提供一个hash方法?这个hash方法又有什么不同?
以下是hash方法的源代码:
Java代码 ![]()
static int hash(int h) {
h ^= (h >>> 20) ^ (h >>> 12);
return h ^ (h >>> 7) ^ (h >>> 4);
}
hash方法是对已给出hashCode值的补充,用于防止那些质量较差的hash函数。并且将此hash函数作为已给定的hashCode的一个补充,可以提高hash值的质量。hash质量的好坏是非常重要,
HashMap用2的次幂作为表的hash长度,这就容易产生冲突。注意:Null 的key的hash值总是0,即他在
table的索引值永远为0。
hash方法如何提高hash值的质量,通过以下实例就会很好的了解。
1)初始化一个HashMap实例,指定容量为16:
Java代码 ![]()
Map map=HashMap(16);
2)向此实例中添加几个元素,它们key的hashcode分别为12,28,44和92。
3)通过indexFor方法可以计算出该key所应存储的下标位置,如果只是通过key的hashcode来计算的话,得出结果为:
| key的hashCode | 二进制值 | length-1二进制值 | 计算后下标位置 |
| 12 | 1100 | 1111 | 12 |
| 28 | 11100 | 1111 | 12 |
| 44 | 101100 | 1111 | 12 |
| 92 | 1011100 | 1111 | 12 |
4)从结果可以看出虽然每个key拥有不同的hashCode,但是通过计算后它们却被分配到了同一下标位置,这显而易见不是我们想要的结果。
原因就在于indexFor方法的设计思路是“按位与”,这样计算过程中无论是0&1还是1&0结果都是0.所以几个key的二进制值与 15的二进制值(1111)进行“与”操作时,实际就相当于只计算了最后四位有效位(红色部分),最终出现了上述结果。
hash函数正是为了避免这一点:
| key的hashCode | 二进制值 | hash计算后 | length-1二进制值 | 计算后下标位置 |
| 12 | 1100 | 1100 | 1111 | 12 |
| 28 | 11100 | 11101 | 1111 | 13 |
| 44 | 101100 | 101110 | 1111 | 14 |
| 92 | 1011100 | 1011001 | 1111 | 9 |
这样就可以很好避免了冲突,以致于所添加的元素能够均匀的分布在整个table数组里,从而提高了HashMap的性能。
至此两篇关于HashMap的文章均已结束,希望能给朋友们带来一些帮助,如文章中出现那些错误还请雅正。