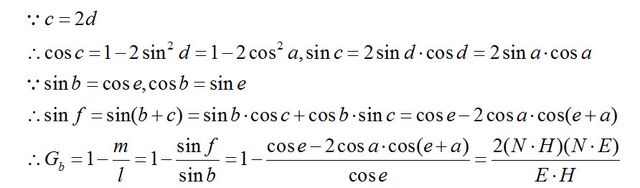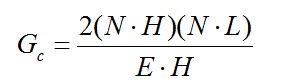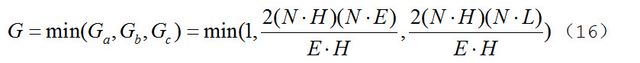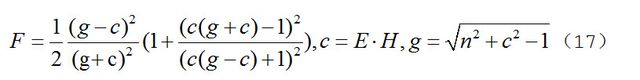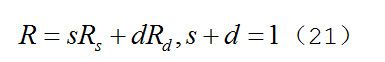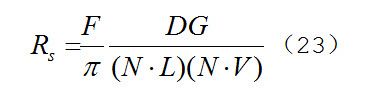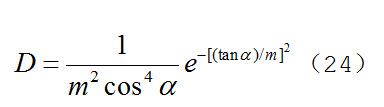cook torrance
http://www.twinklingstar.cn/2013/213/torrance-sparrow-and-cook-torrance-light-model/
一.Torrance-Sparrow光照模型
L,指向光源的单位向量;
N,平面的单位法向量;
E,指向观察者的单位向量;
H,指向V与L的角平分线方向,单位长度,H=(L+V)/|L+V|;
假设平面是由一批像镜子一样的微平面构成的,设想反射光中的镜面分量来自于那些朝向是H的微平面,漫反射分量来自于微平面间的多次反射和内部散射,镜面反射分量是四个因子的组合,如等式(14)所示。
D是平面上各个微平面方向的分布函数。镜面反射光主要来自局部法向量指向H的微平面,Torrance-Sparrow采用的分布函数是一个高斯函数,如等式(15)所示。C1是分布函数的标准差,直接影响平面的属性,它的值越大,平面越粗糙,值越小,平面越平滑。这里α=cos-1(N•H):
图12 凹槽模型
镜面反射光的强度与指向H的微平面量成正比,如果平面被倾斜,则观察者可能看到更多的平面面积。提高的观察面积与倾斜角的cos值成反比,这里说的倾斜角是指平面法向量N与眼睛方向E之间的夹角。这就说明了等式(14)中除以因子N•E。
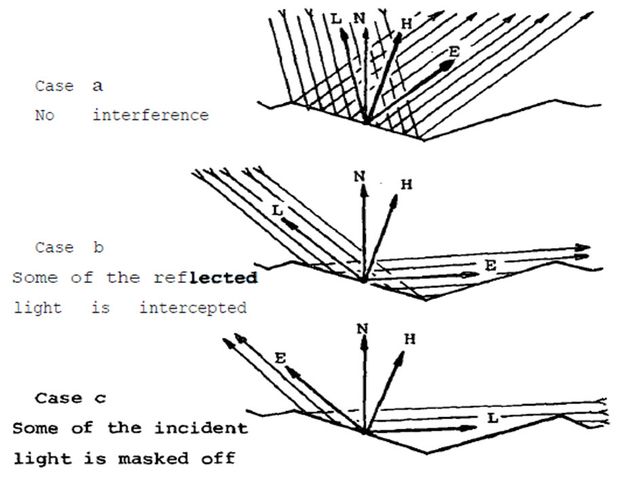
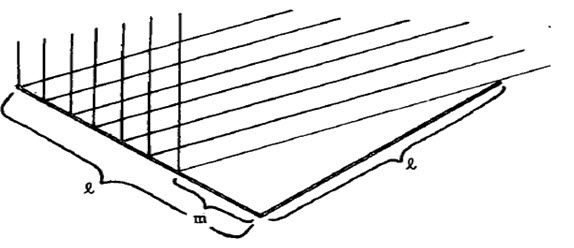
各个微平面之间,可能发生光线的互相阻挡,这里再引入一个几何衰减因子(Geometrical Attenuation Factor),G。它的取值范围是[0,1],表示发生阻挡后剩下的反射光。假设存在两条边相等的凹槽,如图12所示。
图13 m/l比例的光线被阻挡
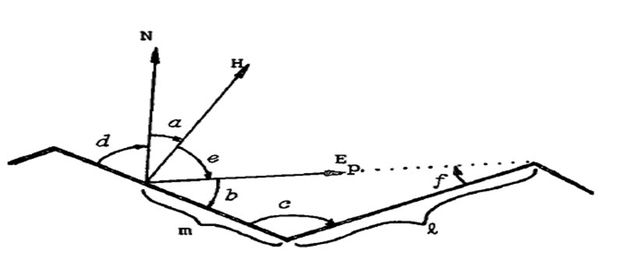
图14 计算m/l的值
图12中的第一种情况,未发生阻挡,所以Ga的值为1.0。对于第二种情况,可以用图13表示,其中m/l比例的光线被阻挡,实际反射出去的光线占比为1-m/l。计算m/l的值,如图14所示,推导过程如下所示:
对于第三种情况,同理可得到
G取Ga,Gb,Gc三个中的最小值,即
最后一个因子是菲涅耳系数(Fresenl Coefficient),如等式(17)所示,其中n表示平面的折射率:
论文【1】中,实验给出了Phong模型和Torrance-Sparrow模型实验结果的结比,如图15所示,具体的参数,参考具体的论文。Phong光照模型的叙述,详细见文章《Phong光照模型》。
图15 Phong模型和Torrance-Sparrow模型对比
二.Cook-Torrance光照模型
图16 反身的几何模型
图17 立体角
参考论文【2】,图16表示反射的几何模型。入射光线的能量可以用等式(18)表示,其中Ei表示入射光线的能量,N平面的法向量且是单位长度,dwi一束入射光线的立体角,Ii表示入射光线的平均强度。立体角的解释参见【4】所示,这里引用书【5】中关于立体角的解释,参见图17,为了简化,该参数一般用一个较小的常量来表示。
在反射方向上的反射光强度与入射方向上的入射光强度成一度比例,(Bidirectional Reflectance Distribution Function,BRDF),参见【3】,可以表达成等式(19),其中Ir表示反射光的强度,R表示双向反射分布函数。因此观察者观察到的反射强度如等式(20)所示:
双向反射分布函数可以分解成镜面反射分量和漫反射分量,因此双向反射分布函数可以表示成等式(21)所示:
除了光源直接的光照外,一个对象还可能接收背景或者环境光的光照,加上环境光的影响,论文【2】中提出的模型用等式(22)来表示:
其中,镜面反射分量Rs表示如等式(23)所示:
对于因子D,Cook-Torrance采用了Beckmann分布函数,如等式 (24)所示,它的功能与Torrance-Sparrow模型中采用的高斯函数类似,它的优点是未引入随机常量,但是运算量更大,m值越大表示表面越光 滑,反之表示表面越粗糙。其它几个因子可以参见第三节的叙述。
为了简化模型,把Rd当作垂直于反射平面的发光双向分布函数,例如Rd=F0/PI(PI=3.141592…) ,即F0即指等式(17)中的c=1的情况,Ra=PI•Rd。s,d,m的取值依赖于反射平面的材质,dwi通常取一个较小的值,比如0.0001。
三.参考
【1】 Paper(James F. Blinn)“Models of Light Reflection For Computer Synthesized Pictures”
【2】 Paper(Robert L.Cook,Kenneth E.Torrance)“A Reflectance Model For Computer Graphics”
【3】 http://en.wikipedia.org/wiki/Bidirectional_reflectance_distribution_function
【4】 http://en.wikipedia.org/wiki/Solid_angle
【5】 《Computer Graphics Using OpenGL,Second Edition》