Decision Trees 笔记

Decision Tree(决策树)属于监督学习算法, 训练过程根据训练集各个属性的不同取值进行逐层划分, 每一层都是对一个属性的划分, 直至节点中的所有样本都为同一个标签(label), 从而构建出决策树; 决策时从树的根节点往下遍历, 直至叶子节点, 当前节点的标签(labe)属性就是测试样本的标签(label).

优点	计算复杂度不高, 输出结果易于理解, 对中间值缺失不敏感; 建树过程无需参数设置及领域知识
缺点	可能会产生过度匹配的问题
适用数据类型	数值型, 标称型

基础概念
1. 熵(Entropy) : 信息的期望值, 用于描述系统的混乱程度(越大越混乱) 
2. 每次划分应当取得最大信息增益, 即使系统以最快速度趋于稳定
3. 熵的计算公式: (对于一个集合, 它的第i个可能取值为 Xi, 取第i个值的概率为 p(i))

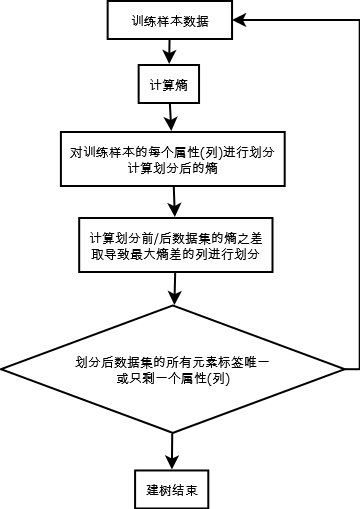
算法描述(本文使用 ID3 算法 )
1. 计算当前集合的熵
2. 对集合的每一个属性(列), 计算按此属性划分后的新集合的熵
3. 对信息增益最大的划分作为当前划分(信息增益越大, 表示新集合越趋向有序)
4. 对一个属性(列)进行划分: 这个属性的每一个取值都是一个新的节点
5. 至一个节点中的所有样本都为同一个分类, 或只剩下一个属性(列)时停止划分.
6. 可以看到 Decision Trees 是有训练阶段的, 所以需要能把建好的树保存到磁盘, 并能重新载入, 以避免每次都要重新计算
7. (补充, 书本 P160) ID3每次选取当前最佳的特征来分割数据, 并按照该特征的所有可能取值来切分. 也就是说, 如果一个特征有 4 种取值, 那么数据被切成 4 份. 一旦按某特征切分后, 该特征之后的算法执行过程中将不会再起作用.

算法流程图(建树)

代码

# -*- coding: utf-8 -* 
from math import log
import operator
import copy

# 数据集
# 第一列表示"不浮出水面是否可以生存"
# 第二列表示"是否有脚蹼"
# 第三列表示"是否属于鱼类"
def createDataSet():
    dataSet = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no' ],
               [0, 1, 'no' ],
               [0, 1, 'no' ]]
    labels = ['no surfacing','flippers']
    return dataSet, labels


# 计算一个数据集的'香农熵'
def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    # 统计各个属性出现次数
    for featVec in dataSet: 
        currentLabel = featVec[-1]      # -1 表示最后一列
        if currentLabel not in labelCounts.keys(): 
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1

    # 出现次数/总行数 即为频率 prob
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2) # 以 2 为底计算对数
    return shannonEnt
 

# 按照给定特征划分数据集, 即把 dataSet 中第 axis 列值为 value 的行取出来作为一个新集合
# 新取出的行不包括第 axis 列 
def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]   # reducedFeatVec 不包含第 alis 列
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet
    

# 选择最好的数据集划分方式, 即划分后的信息增益值最大, 即熵最大; 返回符合划分的列下标
def chooseBestFeatureToSplit(dataSet):
    # numFeatures 为 dataSet 总列数-1, 最后一列是标签(label), 不参与划分
    numFeatures = len(dataSet[0]) - 1  

    baseEntropy = calcShannonEnt(dataSet)  # 原始熵
    bestInfoGain = 0.0; 
    bestFeature = -1

    # 对每一列计算按其划分后的熵, 取熵最大时的列
    for i in range(numFeatures):       
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)       
        newEntropy = 0.0
        # uniqueVals 为第 i 列的所有可能取值
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)     
        
        # 计算划分后的信息增益, 确保划分后增益最大
        infoGain = baseEntropy - newEntropy    
        if (infoGain > bestInfoGain):       
            bestInfoGain = infoGain         
            bestFeature = i
    return bestFeature                     


# 将 list 中的每个元素及出现次数映射成 map
# 返回出现次数最多的元素
def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(), 
                              key=operator.itemgetter(1), 
                              reverse=True)
    return sortedClassCount[0][0]


# 递归创建决策树, 停止条件: 类别完全相同
def createTree(dataSet,labels):
    # 最后一列是类别, 当类别完全相同时, 停止建树
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList): 
        return classList[0]

    # 如果数据集只有一列, 则这一列中出现最多的标签(label) 就是此节点的 label
    if len(dataSet[0]) == 1: 
        return majorityCnt(classList)

    # 找出最适合拆分的属性下标
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])       # 每个 label 只会被用来划分一次

    # 根据此属性的不同值, 划分成不同节点, 再对每个节点递归建树
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]       
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, 
                                                               bestFeat, 
                                                               value),
                                                  subLabels)
    return myTree                            
    

# 判断某个 testVec 属于哪个 label, 递归遍历树
def classify(inputTree,featLabels,testVec):
    firstStr = inputTree.keys()[0]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)
    key = testVec[featIndex]
    valueOfFeat = secondDict[key]

    # 如果是字典, 表示可以递归, 否则就是到叶子节点了, 返回当前节点的 label 即可
    if isinstance(valueOfFeat, dict): 
        classLabel = classify(valueOfFeat, featLabels, testVec)
    else: classLabel = valueOfFeat

    return classLabel


# 保存决策树到文件中
def storeTree(inputTree,filename):
    import pickle
    fw = open(filename,'w')
    pickle.dump(inputTree,fw)
    fw.close()
    

# 从文件读取决策树
def grabTree(filename):
    import pickle
    fr = open(filename)
    return pickle.load(fr)
    

    
if __name__ == "__main__":
    myDat, labels = createDataSet()
    tree =  createTree(myDat, copy.copy(labels))  # 复制 labels 后才作为参数
    print tree
    print classify(tree, labels, [1, 1])
#    print calcShannonEnt(myDat)

说明
本文为《Machine Leaning in Action》第三章(Splitting datasets one feature at a time: decision trees)读书笔记, 代码稍作修改及注释.

好文参考
1.《算法杂货铺——分类算法之决策树(Decision tree)》