HDU1025 Constructing Roads In JGShining's Kingdom

                             Constructing Roads In JGShining's Kingdom

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 11914    Accepted Submission(s): 3393

Problem Description

JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.

Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.

With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.

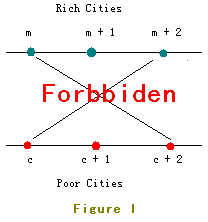
Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.

The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.

But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.

For example, the roads in Figure I are forbidden.



In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^

 

Input

Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to the end of file.

 

Output

For each test case, output the result in the form of sample.
You should tell JGShining what's the maximal number of road(s) can be built.

 

Sample Input

   
   
   
   

    
    
    
    2 1 2 2 1 3 1 2 2 3 3 1
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    Case 1: My king, at most 1 road can be built.  Case 2: My king, at most 2 roads can be built.  
    
    
    
    
 
     
 
      Hint 
     
 Huge input, scanf is recommended. 
    
    
    
    
     
   
   
   
   

 

Author

JGShining（极光炫影）


解题思路：一看就知道是求最长子序列有木有，动归有木有。好吧，我承认我超时过，题目数据量比较大an integer n(1 ≤ n ≤ 500,000).如果用经典的最长子序列求法，会超时。
            对于题意，处理时可以化简，每对城市（x即缺资源的，y即自愿丰富的）输入后可以直接处理到数值ct[]中，ct[x]=y.这样就把问题转变成求序列ct[]的最长递增子序列。
           用LIS算法求最长子序列，不用历遍前面各子序列的最长子序列，节约时间。直接用栈存储当前最长子序列的值，最后最长子序列的长度为栈的长度。这里我用数组模拟栈。对于每个元素Y（x已经递增），检索它与数组中已存储的最长子序列的元素的关系（数组最后元素road[max1-1]）：（1）若ct[x]>road[max1-1],则直接将ct[x]存储到数组后面即可(入“栈”)，这里不用解释啦，可以直接增长最长子序列的长度。（2）若（1）不成立，则查找road中第一个（从“头”开始）比ct[x]大的元素（二分法），并替换它即可（置换），可增加后面元素的“可入栈性”。这个不好直接讲清楚，我们上案例：
ct[x ]
x    1    2    3    4    5    6    7    8
y    2    5    1    3    4    6    8    7

则对于栈的模拟数组road[ max1 ]：  



最后，最长子序列为max1-1（每存入一个元素都max++）。                           

#include<stdio.h> int ct[500005]; int road[500005]; int lown(int i,int x)   //二分查找第一个比x大的元素在road中的下标位置 {     int j=0;     while(j<=i)     {         int m=(i+j)>>1;         if(x<road[m])             i=m-1;         else if(x>road[m])             j=m+1;         else             return m;     }     return j; } int main() {     int t=1;     int n;     int i,j;     int max1;     while(scanf("%d",&n)!=EOF)     {         max1=0;         int x,y;         for(i=0;i<n;i++)         scanf("%d%d",&x,&y),ct[x]=y;   //转化为求ct的最长递增子序列         road[max1++]=ct[1];         for(i=2;i<=n;i++)         {             if(ct[i]>road[max1-1])    //入“栈”                 road[max1++]=ct[i];             else                 road[lown(max1-1,ct[i])]=ct[i];     //置换         }         printf("Case %d:\n",t++);         printf("My king, at most %d road",max1);         if(max1!=1)         printf("s");    //最长子序列长度大于1时，要用复数形式（加‘s’）         printf(" can be built.\n\n");     }     return 0; }