从有限状态机（FSM）到行为树（Behavior Tree）（1）

转自http://www.aisharing.com/archives/439

选这次主题，要感谢一位网友的来信，他询问了一些如何将有限状态机转成行为树的问题，当时，我回信给了一些建议，但后来我仔细想了一下，觉得可能说得还不够全面，所以我就想通过这篇文章，来整理出一些比较典型的转化“模板”，给有这方面疑惑的朋友一些帮助，如果有朋友有一些自己的见解的，可以在后面留言，我们一起讨论。

有限状态机维护了一张图，图的节点是一个个的状态，节点和节点的连线是状态间根据一定的规则做的状态转换，每一个状态内的逻辑都可以简要描述为：

如果满足条件1，则跳转到状态1
如果满足条件2，则跳转到状态2
…
否则，不做跳转，维持当前状态

稍作整理的话，我们可以对状态机的几种跳转的情况一一描述出来，然后看看如果将这些情况用行为树来表示的话，可以怎么做。这就是我前面说的“转化模板”，当然我不能保证我下面列出的是状态机的所有可能情况，如果大家在实践中发现还有其他的情况，欢迎留言，我随时更新。

在这之前，我们可以先回忆一些关于行为树的一些概念（可以参考1，2）

• 控制节点：选择节点，序列节点，并行节点，等等

• 行为节点：两种运行状态，“运行中”和“完成”

• 前提条件

模式1：当处在任何状态中，一旦某条件满足，即跳转到某个特定的状态。

比如，在状态机中的一些错误处理，经常会用到上面的这种模式，当状态在运行过程中，发生了某些异常，那一般，我们会把状态机跳转到某个异常状态。这种情况，我们可以用到带优先级的选择节点（Priority Selector）方式，如下图，可以看到，我们把状态c作为行为树里的行为节点，跳转条件（Condition1）作为这个节点的前提（Precondition）。

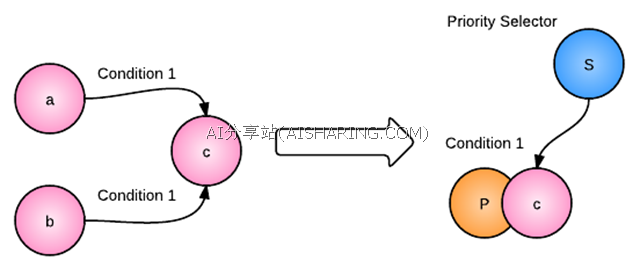
再用上面举到的错误处理的例子，在状态机中，我们一般会这样写：

 1: STATE A::Update()

 2: {

 3:     ...

 4:     if(error)

 5:     {

 6:         return TO_ERROR_STATE();

 7:     }

 8:     ...

 9:     return UNCHANGED_STATE();

 10: }

转换到行为树中，我们会通过外部的黑板来做通信（可以参考这里），在行为节点a中，我们会这样写

 1: EXECUTE_STATE A::Execute(BlackBoard& out)

 2: {

 3:     ...

 4:     if(error)

 5:     {

 6:         out.error = error;

 7:         return EXECUTE_STATE_FINISH;

 8:     }

 9:     ...

 10:     return EXECUTE_STATE_RUNNING;

 11: }

然后对于节点c的前提里，我们来读取黑板里的error值

 1: bool Condition1::IsTrue(const BlackBoard& in) const

 2: {

 3:     return in.error == true;

 4: }

模式2：对于同一个跳转条件，处在不同的状态会有不同的跳转

比如，我们有两个状态，a和b，他们都对同一个跳转条件作出响应，但和模式1不同的是，a对跳转到状态c，而b会跳转到状态d，换句话说，这是一种带有上下文的状态跳转方式。对于这种情况，可以用到序列节点的相关特性，如下图

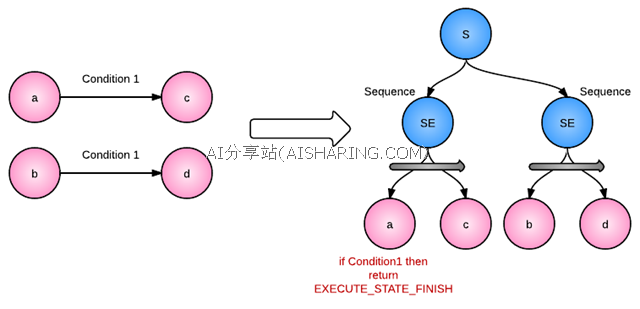
序列节点中，当前一个节点运行完成后，会执行下一个节点，利用此特性，在上图中可以看到，我们在a中，当满足条件Condition1的时候，则返回“完成”，那行为树就会自动跳转到c节点中，参考代码如下：

 1: EXECUTE_STATE A::Execute(BlackBoard& out)

 2: {

 3:     ...

 4:     if(condition1 == true)

 5:     {

 6:         return EXECUTE_STATE_FINISH;

 7:     }

 8:     ...

 9:     return EXECUTE_STATE_RUNNING;

 10: }

对于这种模式的另一种转化，可以不用序列节点，还是用到选择和前提的组合，但我们在前提中加上一个当前状态的附加条件，如下图

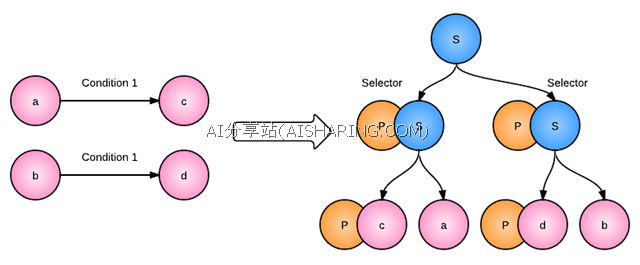
在第二层的前提中，我们可以这样写

 1: bool InACState::IsTrue(const BlackBoard& in)

 2: {

 3:     return in.current_running_node = A::GetID() ||

 4:            in.current_running_node = C::GetID();

 5: }

 6: bool InBDState::IsTrue(const BlackBoard& in)

 7: {

 8:     return in.current_running_node = B::GetID() ||

 9:            in.current_running_node = D::GetID();

 10: }

这样对于c的前提就是Condition1和InACState的“与”（回想一下前提的相关内容）。由于我们保留了上下文的信息，所以通过对于前提的组合，我们就转化了这种模式的状态机。

（待续…）