cocos2dx 中各种运动和速度

猴子原创，欢迎转载。转载请注明出处，谢谢！

原文地址：http://blog.csdn.net/yanghuiliu/article/details/7261808

在实现运动中，我们常常需要实现一些加速度或者减速度的效果，cocos2d-x引擎为我们提供了相应的实现接口，这样我们就不用再用原来的公式计算方法来实现加减速度的效果

Ease系列的方法改变了运动的速度，但是并没有改变总体时间，如果整个的action持续5秒钟，那么整个的时间仍然会持续5秒钟。

这些action可以被分成3类：

In actions: action开始的时候加速

Out actions: action结束的时候加速

InOut actions: action开始，结束的时候加速

第一个参数为要加减速度的动作，第二个为加减的速率

还有一些特殊的缓冲公式继承了进来

1.指数缓冲

 

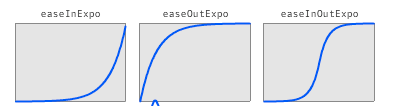
EaseExponentialIn

EaseExponentialOut

EaseExponentialInOut

2.赛因缓冲

 

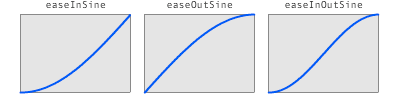
EaseSineIn

EaseSineOut

EaseSineInOut

 

3.弹性缓冲

 

EaseElasticIn

EaseElasticOut

EaseElasticInOut

4.跳跃缓冲

 

EaseBounceIn

EaseBounceOut

EaseBounceInOut

5.回震缓冲

 

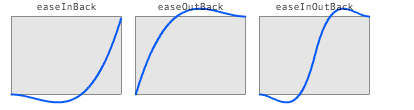
EaseBackIn

EaseBackOut

EaseBackInOut

另外还可以设置速度的倍数

通过把动作定义为CCSpeed并改变速度，使用setSpeed将速度按参数的倍数变大或者缩小,这样可以手动实现加减速度

尊重作者劳动，转载时请标明文章出处。
作者：Bugs Bunny
地址：http://www.cnblogs.com/cocos2d-x/archive/2012/03/13/2393898.html

本文函数图像使用GeoGebra绘制，感谢它才华横溢的作者。

为了方便用户灵活地控制精灵运动，cocos2d-x提供了CCActionEase类系的动作。它们拥有相似的名字――CCEaseXxxxIn、CCEaseXxxxOut、CCEaseXxxxInOut，同时也拥有相似的行为――速度由慢至快、速度由快至慢、速度先由慢至快再由快至慢。但是除了这些，我们对CCActionEase一无所知。就算查阅参考手册，我们能得到的信息也不过是类似Ease Sine In的简短说明。它们究竟是什么模样，我们该如何选择？

今天我们就来解决这个问题。鉴于CCActionEase类系的庞大，文章可能会分成两到三篇。

1)CCEaseSineIn

在《cocos2d-x动作系统浅析》一文中提到：
update函数接受一个百分比参数，它表示动作的完成进度。update根据这个百分比将目标对象做出相应的调整。
可以说这个update函数就是CCActionEase的灵魂。

  CCEaseSineIn::update(ccTime time)
 {
     m_pOther->update(- * cosf(time * ()M_PI_2) + );
 }

之前我们已经知道CCActionEase类系的动作就是调整其他动作的速度，变换出新的效果。这里的m_pOther就是那个被影响的动作，而一切魔力的源头就在它接受的参数上。CCEaseSineIn将传入的百分比参数进行了一系列变换，然后传给了m_pOther。

我们将这个变换公式提取出来，记作：
f(x)=1-cos(π/2*x) x∈[0,1]
这个就是已用时间百分比与实际完成进度的关系。在匀速运动中，它们应该是相等的，但是在变速运动中，它们的关系就会变幻莫测。

上图中的黑色曲线就是f(x)的函数图像。它的定义域从0开始，到1结束，值域也是这样。根据这条线的走势，可以粗略看出速度是越变越快的，但还是不够形象。
在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。如果我们能得到这条瞬时速度的曲线，那就直观多了。上面的函数f(x)是已用时间百分比与实际完成进度的关系，这里可以近似地理解为时间与路程的关系。
所以我们对f(x)求导，得出：
f'(x)=π/2*sin(π/2*x) x∈[0,1]
它对应图中那条红色曲线。可以很明显地看出，速度越变越快，在C点达到了最高。
正如它名字说的那样，它的速度由慢至快，呈正弦变化。

2)CCEaseSineOut

我们再来看下CCEaseSineOut类。

  CCEaseSineOut::update(ccTime time)
 {
     m_pOther->update(sinf(time * ()M_PI_2));
 }

同理得出：
f(x)=sin(π/2*x) x∈[0,1]
f'(x)=π/2*cos(π/2*x)

同样我们更关注那条红色曲线，它从最高点C出发，一路下降到达A点。这表明在CCEaseSineOut动作中，速度是越来越慢的，它的图像也呈正弦变化。

3)CCEaseSineInOut

我们知道CCEaseXxxxInOut的速度变化是先由慢至快，再由快至慢。如果我们将上面两个图像拼在一起，然后在将横轴比例缩小一倍，那结果就是这条曲线的模样了。
一般情况下，我们需要将函数分成两段，第一段在0到0.5之间，第二段在0.5到1之间。我们来看看CCEaseSineInOut是如何实现的。

  CCEaseSineInOut::update(ccTime time)
 {
     m_pOther->update(- * (cosf(()M_PI * time) - ));
 }

f(x)=-0.5*(cos(π*x)-1) x∈[0,1]
f'(x)=π/2*sin(π*x)

在CCEaseSineInOut中，这两段曲线正好是同一个函数（非分段函数）的图像。很巧妙是不是？
图中红色曲线从原点O出发，一路上升到达最高点C，然后又一路下滑降至D点。它同样也是一条正弦变化的曲线。动作的速度看起来就是由慢至快，再由快至慢的。

小结

CCEaseSineIn、CCEaseSineOut、CCEaseSineInOut这三个动作同属速度正弦变化，变化的范围是[0,π/2]。

4)CCEaseExponentialIn

有了前面的经验，后面就容易多了，先来看一下CCEaseExponentialIn的update函数。

  CCEaseExponentialIn::update(ccTime time)
 {
     m_pOther->update(time ==  ?  : powf(,  * (time/ - )) -  * );
 }

大家可能已经注意到，这里使用了一个条件运算符，于是表达式变作了分段函数。
当x=0时，f(x)=0
当x∈(0,1]时，f(x)=2^(10*(x-1))-0.001

注意这条不是速度的曲线。
上面副绘图区中的图像就是这个函数的整体走势，我们在主绘图区给原点附近的曲线一个特写。可以看到，除了x=0的情况，曲线与x轴还有一个交点。
对2^(10*(x-1))-0.001=0求解，得出：
x=1-ln(1000)/(10*ln(2))=0.00342

现在我们开始在脑中想象一下精灵按照CCEaseExponentialIn动作移动的详细步骤。
首先，时间从零开始，精灵被设置到起始位置。这一步是正常的没有问题。
接下来，精灵猛地朝着反方向跳动了很小的一段距离。这个距离是非常非常小的，也就是图上的B点附近，大约只占整个移动距离的0.00234%
然后，精灵开始以变化的速度朝着目标点移动。经过点A时精灵回到初始位置。这时，我们设计的运动才刚刚开始。
如果我们将x=1代入公式，可以推算出：
f(x)=1-0.001=0.999
也就是说，图像最终没有到达终点，而是差了一小段距离。

简单来说，总时间的前0.342%部分以及最终的那一瞬间的运动是不太正常的。
如果你设计了一个超过1000秒的运动，那么前3秒内，精灵的准确位置不会在你设计的轨迹上。
当然如果想观察到这个问题，运动的距离也是一个关键。
假设你疯狂地设计了一个运动10万像素的精灵，并且运动时间超过1000秒，那你就能观察到这一现象了。3秒钟，反向2个像素。

但是为什么会这样呢？是引擎的bug吗？
确切来说，这应该算不上是bug，这只是精度引起的问题。

下面这段都是我自己的推测，也就是猜到，大家看看就好了。
我猜测这个公式的最初原型应该是：
f(x)=2^(10*(x-1)) x∈[0,1]
但是它有一个问题，那就是当x=0的时候，f(0)=1/1024
时间为零的时候，精灵大约就已经有了千分之一的位移，而且是在一个物体运动刚开始的时候，猛然地跳动是非常明显的。所以设计者将千分之一的误差移动到了末尾，也就是运动要结束的时候。
那公式现在的样子就是：
f(x)=2^(10*(x-1))-1/1024 x∈[0,1]

大家都知道cocos2d-x多使用单精度浮点型数字，以及写0.0009765625f比较麻烦等诸多因素，最后这个公式就简化成了现在的模样。

我的猜想说完了，我们接着来求导：
f'(x)=10*2^(10*(x-1))*ln(2) x∈[0,1]

按照最理想的那个公式绘制出图像，这里我们只看那条红色的曲线。这条曲线从D点开始一路上升，迅速到达C点。如果你对它再次求导，就能得出其加速度的变化规律。从DC曲线上应该可以看出其加速度也是越来越大的。
额，说得有点儿远了。我们把注意力先集中起来，计算出速度的最小值和最大值。
f'(0)=10*2^(-10)*ln(2)=0.006769
f'(1)=10*2^0*ln(2)=6.931472

CCEaseExponentialIn的速度由慢至快，从0.006769上升至6.931472，呈指数级变化。

5)CCEaseExponentialOut

  CCEaseExponentialOut::update(ccTime time)
 {
     m_pOther->update(time ==  ?  : (-powf(, - * time / ) + ));
 }

CCEaseExponentialOut与CCEaseExponentialIn的实现是相似的，唯一的不同是CCEaseExponentialOut在最后一瞬间会有短距离的跳跃（千分之一的误差），而CCEaseExponentialIn是舍弃部分。个人认为CCEaseExponentialOut的处理方式更合理些。
好了直接上图

这里没有难点，我直接让工具生成的导函数图像。
我们关心的是A点(0,6.93147)和D点(1,0.00677)，与CCEaseExponentialIn的速度范围是一样的。从6.93147下降至0.00677，速度为由快至慢的指数变化。

6)CCEaseExponentialInOut

在《知易游戏开发教程cocos2d-x移植版003》中有一段CCEaseExponentialInOut的演示代码，测试运行时会发现精灵最后以极快的速度飞出了屏幕，是笔者使用不当，还是别的什么原因？当时由于时间、精力的问题没有深入研究，今天借此机会将问题分析一下。

  CCEaseExponentialInOut::update(ccTime time)
 {
     time /= ;
      (time < )
     {
         time =  * powf(,  * (time - ));
     }
     
     {
         time =  * (-powf(,  * (time - )) + );
     }
 
     m_pOther->update(time);
 }

呵呵，典型的分段函数。绘制函数图像如下：

图中这条蓝色的曲线就是CCEaseExponentialInOut使用的分段函数。很明显可以看到在A点处，曲线走向发生了90°的变化，向着点(1,-511)延伸。它没有像前面说过的函数那样逼近点C(1,1)，这就解释了为什么精灵莫名其妙地飞出了屏幕。

这是一个bug，我们希望曲线的后半段能像那条绿色的曲线AC那样。（我只在Win32平台上测试的，不知其他平台上是否也存在这个问题，有兴趣的朋友可以测试下。）

我的修改如下：

  CCEaseExponentialInOut::update(ccTime time)
 {
     time /= ;
      (time < )
     {
         time =  * powf(,  * (time - ));
     }
     
     {
                  time =  * (-powf(,  * ( - time)) + );
     }
 
     m_pOther->update(time);
 }

修正后，动作的行为正常了。
对新的函数求导，得出图中的红色曲线。其中点D、点E、点F的坐标分别为(0.5,6.93147)、(0,0.00677)、(1,0.00677)。
细心的朋友可能已经发现了点C没有到达(1,1)。是的，这里存在0.000488的误差，曲线的起始点也一样。即原来1/1024的误差被平分到了开头和末尾。

小结

CCEaseExponentialIn、CCEaseExponentialOut、CCEaseExponentialInOut这三个动作同属速度指数级变化，变化的范围是[0.00677,6.93147]。