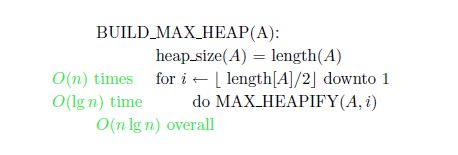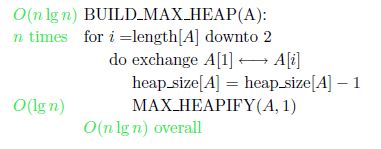MIT Introduction to Algorithms 学习笔记(五)

Lecture 4: Heaps and heap sort

1.堆(Heap)

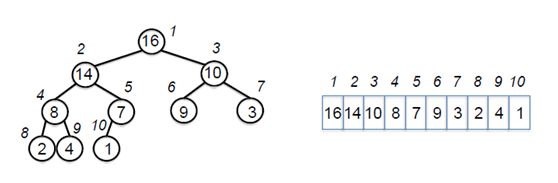
堆是一个数组对象，可以看作是一个类完全二叉树(nearly complete binary tree)。

堆的一些操作:

root of tree: first element in the array, corresponding to i = 1

parent(i) =i/2: returns index of node's parent

left(i)=2i: returns index of node's left child

right(i)=2i+1: returns index of node's right child

 

python代码：

def parent(i):
    return i // 2


def left(i):
    return 2*i


def right(i):
    return 2*i + 1

#A的第一元素不算在总长度内，相当于A的index从1开始
def heap_size(A):
    return len(A) - 1

 

最大堆(Max-Heaps):

对于每个节点i都有A[PARENT(i)] ≥ A[i].

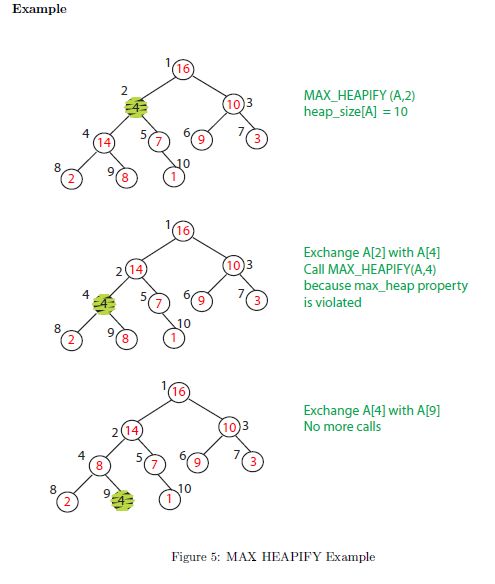
MAX HEAPIFY: O(lg n) maintains max-heap property

 

python代码：

#O(lg n) maintains max-heap property    
def Max_Heapify(A,i):
    l = left(i)
    r = right(i)
    
    if(l <= heap_size(A) and A[l] > A[i]):
        largest = l
    else:
        largest = i
        
    if(r <= heap_size(A) and A[r] > A[largest]):
        largest = r
    
    if(largest != i):
        tmp = A[i]
        A[i] = A[largest]
        A[largest] = tmp
        Max_Heapify(A, largest)
        
    return

 

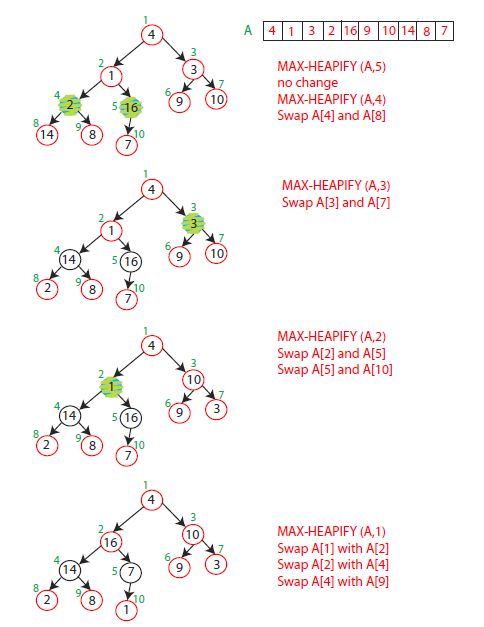
BUILD MAX HEAP: O(n) produces max-heap from unordered input array

为什么从n/2开始?

Elements A[n/2 ……n] are all leaves of the tree and can’t have children.

python代码：

def Build_Max_Heap(A):
    for i in range(heap_size(A) // 2,0,-1):
        Max_Heapify(A, i)
    return

 

 

 

2.堆排序(Heap-Sort)

排序过程:

• Build max heap from unordered array

• Find maximum element (A[1])

• Put it in correct position A[n],A[n] goes to A[1] New root could violate max heap property but children remain max heaps.

• Discard node n from heap (decrement heapsize)

 

Heap Sort Algorithm

python代码：

def Heap_Sort(A):
    L = []  
    Build_Max_Heap(A)
    iSize = heap_size(A)
    for i in range(iSize,1,-1):
        tmp = A[i]
        A[i] = A[1]
        A[1] = tmp
        L.insert(0, A.pop())
        Max_Heapify(A, 1)
        
    return L