leetcode十一题----Container With Most Water

         leetcode第11题，个人觉得还是蛮有意思的。

         首先是英文题目：Given n non-negative integers a1, a2, ..., an, where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water。

        翻译一下就是：有n个点在横坐标上，分别对应n个数:a1,a2...an每个数都有自己的值，这个值对应这个点的纵坐标高度（也就是说在这个点上的线的高度），任意两个点和横坐标组成一个桶，编一个程序出来，求给出n个大小来，求出容量最大的桶的盛水量。

       画一下图就是这样：（比如给出的3个数，分别为2，4，5）（图有点丑。。。）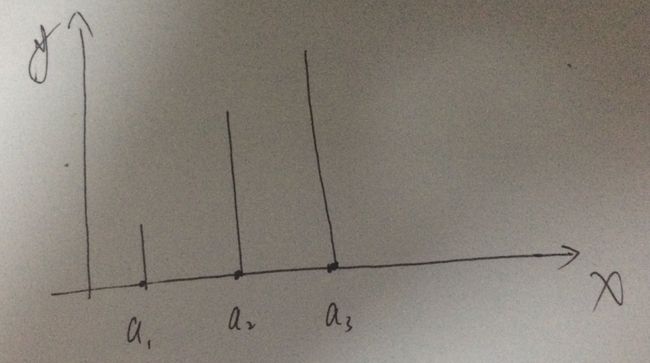


 
可以很容易看到，a1-a2的桶容量是2，a2-a3容量是4，a1-a3容量也是4。

     这种题目用程序怎么做？ 首先肯定是找规律。桶的大小由谁判断？  横坐标差和两个坐标中较小的纵坐标。既然是找最大容量的，那么就应该从两头开始往中间找（因为两头的横坐标差最大，所以只需要比较纵坐标即可），怎么找？ 记得以前学算法的时候经常用到的一个两头指针，在这里也用到了。既然是找最大容量了，而现在横坐标差已经是最大了，那么就应该找纵坐标的麻烦了。。  因为容量是由两个坐标中较小的纵坐标决定的，那么只比较较小的纵坐标即可了。

         程序的算法是这样的：

          1，第一步，先假设桶的最大容量就是横坐标差最大的那两个坐标围成的桶（上例中的a1和a3）（这个桶暂叫原桶）

         2，让两个指针中较小的向中间移动（为什么移动较小的，这是因为容量由较小的纵坐标和横坐标决定，如果移动较大的纵坐标，那么无论新点的纵坐标是多少，横坐标差变小了，那么新桶都不可能比现有的桶容量更大）。

        比较两个桶大小，以较大的桶作为原桶，继续2，3，直到两个点相遇.

         这里有一点比较容易想不通：两个点做桶边，应该有n*n-1/2种情况，那么为什么移动n次就决定了最大的桶的容量。

         这里有一点比较关键。 因为我们刚开始取的是最靠边的点，那么这时候横坐标差最大，桶的容量由较小的点的纵坐标决定，假设a1<an，那么桶大小应该为：a1*(n-1)，这时候，只要左边这个点在a1这里，无论右边的点在什么地方，组成的桶都不可能比a1和an组成的桶大（纵坐标小的点决定高度），这就是短板原理。。。

        所以，我们可以这样假设，容易理解一点：点ax和ay组成的桶现在最大，然后Hx<Hy，那么我们移动y点，因为y点右边的点已经都比较过了，所以不用向后移动，我们假设将y点向左移动到x点了，但是桶的容量全都没有xy大（其实不用移动，上面那段话已经说明不管怎么移动都没用，不过这样想的话容易理解一点），那么接下来移动x，向y点移动，每移动一步就比较一次桶的大小，直到找到一个比xy大的桶，组成一个新的xy，然后继续这样。。。

      上一下代码：

/**
 * Test11 :水桶程序
 * 
 * @author xuejupo jpxue@travelsky.com
 * 
 *         create in 2016-1-6 下午7:05:40
 */

public class Test11 {

	/**
	 * main:
	 * 
	 * @param args
	 *            void 返回类型
	 */
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int[] height = {1,2,3,4,5,1};
		System.out.println(maxArea(height));
	}

	/**  
	* maxArea: 求出木桶最大水量
	* 基本思想是这样的：先算出最左边和最右边的木板形成的木桶的水量，然后让较短的木板向中间靠拢
	* 因为：确定较短的木板，那么无论较长木板如何向中间靠拢，都不可能比现在的水量更大
	* @param height
	* @return 
	* int  返回类型   
	*/
	public static int maxArea(int[] height) {
		if(height == null || height.length < 2){
			return 0;
		}
		int left = 0;
		int right = height.length - 1;
		//木桶容量
		int size = Math.min(height[left], height[right]) * (right - left);
		while(left < right){
			int tempSize = Math.min(height[left], height[right]) * (right - left);
			if(tempSize > size){
				size = tempSize;
			}
			if(height[left] < height[right]){
				left ++;
			}else{
				right--;
			}
		}
		return size;
	}
}

 结果：6