L-System之学习总结

 

           鸣谢

 

感谢陆亮同学，是他制作的java程序演示出的多姿多彩的分形才震撼了我，从而让我踏上了学习分形的道路；感谢胡zong，正是他为我们展示了陆亮同学的程序，并以奖励“机器人”为诱惑鼓励我们去研究分形，才使我在研究L-System的过程中享受了一场视觉盛宴。

附陆亮同学研究分形的一篇博客：http://luliangy.iteye.com/blog/1266548

 

         前言

 

         一、海岸线到底有多长？

         最早提出这个问题的好像是Mandelbrot，由于这个问题比较有趣，而且和分形有着比较密切的关联，不妨就放在前言部分来一起聊一聊。如果这时你问我分形是什么，我可以如实回答你——我也不知道，但我可以尽力去描述哪些东西算是分形。不过话说会来，分形是什么有必要知道么？当然没必要，就像筷子，你从来不必研究它到底应该严格定义成什么，只要能用就足够了。

你也许会像我一开始一样持有一种看法（如果你没有这种想法，也不妨看看我当时是怎么想的^_^），中国的海岸线应该是一个有限的长度，其中支持这个结论的我的一个观点就是——中国不就960万平方公里么，再大能大到哪去呢？难道它的周长还能是无限的不成？

于是这样一个看法就抽象成了这样一个命题——对于一个面积有限的平面闭合图形，它的周长应该是有限的，然而真的是这样的么？

后来我用一个数学模型推翻了这个命题。我们不妨用y=sin(wx)(0<x<2*pi)这一部分的正弦曲线与x轴所围成的面积看做我们的国土面积，用微积分公式去推导的话容易得知，如果w取正整数的话，这一面积恒等于2，然而这个曲线的周长呢？会随着w的增加而不断的增加，我们可以直观的认为，w越大这条曲线的局部结构就会越趋于精细。

因此，即便我们的国土面积是有限的，其边缘也必然或多或少具有类似这样的精细的结构，如果我们把这些精细结构边缘的长度都算进去的话，那么很显然，我们的海岸线是无限长的。

那教科书上所谓的中国海岸线的长度是怎么来的呢？自然是在一定的精细程度上用直线拟合了曲线，而忽略掉了一些更为精细的结构，这也便是所谓的“线的长度取决于你用多精细的尺子去量”。

        后来在人们研究类似这样问题的过程中就诞生了分形几何学，分形正是这样一种无穷精细的机构，也是自然界中普遍存在的结构。在现有条件下，我们可以用分形理论在二维空间上模拟出树，在三维空间上模拟出更为复杂的树以及山峦、河流等。

 

        二、一个有趣的序列

       之所以聊一聊下面这个有趣的序列，正是想借此来一起初步感性地感受一下所谓的分形的其中一个特征——自相似。

       这个序列一开始只有一个0，每次我们把这个序列中所有的元素复制一份补到序列的后面，再把复制的元素都增加1，就像这样：

        序列1：0

        序列2：0 1

        序列3：0 1 1 2

        序列4：0 1 1 2 1 2 2 3

        序列5：0 1 1 2 1 2 2 3 1 2 2 3 2 3 3 4

        ……

        这样得到的序列神奇在哪里呢？如果你把这个序列的偶数项都删去的话，你会发现，剩下的序列和没删之前的序列是一模一样的！当然，我们假想这个序列是按这个规则生成的无限长的序列。

        这个序列为我们带来了一个直观的自相似的感性上的感受，再加上前面提到的无穷精细，这样我所认为的分形所具备的两个基本的特征就都介绍给大家了，下面就来聊一聊我们要如何画出二维的分形呢？

  

        正文

 

        一、分形直观的震撼美

既然是美，自然要贴几幅图了，用语言是没办法描述的，正所谓只可意会，不可言传。以下几幅即是我编写的java程序所生成的几幅分形图。

 

 

        二、用L-System的规则生成分形

        L-System分形只是分形中的一小部分，就我目前的研究看来，它只能生成直线段构成的分形，然而真正的分形还包括其他很多的东西，如果有兴趣的话不妨了解一下，这里有个贴图比较多的网站，可以直观的感受一下分形之美。

        http://paulbourke.net/fractals/

        下面为了讨论的方便，我使用了很多诸如“某某规则”一类的语言，然而实际上这些规则都是我自己命名的，因为网上对L-System的介绍的资料很少，所以一些东西就只好由我自己去“下定义”了。

        1．AB规则生成L-System分形

就像前面提到的序列那样，如果我们定义了一个序列的初始长度以及序列的演变规则，那么就可以生成一个具有自相似特征的序列。

比如我们现在有一个母序列只有一个字符A，然后我们分别定义字符A与字符B的演变规则，A->AABA，B->BABA，这样按照这个规则不停地演变，我们就会得到很长的一个具有自相似特征的序列，就像下面这样：

A  ->  AABA  ->  AABAAABABABAAABA  ->  AABAAABABABA……

然而这只是字符串呀，怎么让它变成图形呢？其实只要我们对A、B赋予一定的意义即可。假设我们现在有一个专管画图的小机器人，我们发给它一长串由上面的规则演变成序列，并且告诉它：“如果你遇到一个A，就左转60度，然后往前走一个单位长度，如果你遇到一个B，就右转120度，然后往前走一个单位长度。”这样等小机器人把这个序列读完之后，它的足迹不就是一个图形了么？你不妨在纸上画一画，看看这样会形成一个生么样的图形，当然，在画之前你要明确一点，就是演变的深度你要确定好，比如如果演变深度为0的话，你只需要画一个字符A所产生的图像，如果演变深度为1的话，你就应该画AABA所产生的图像，等等。

当然，其实你可以在我做的My L-System里面选My_AB_L-System，并将上面叙述的参数输进去，计算机就会自动帮你生成图形的。如果你暂时还不清楚要输进去哪些参数，没关系，我在本文的后面还会解释一下，哪些位置应该输入哪些参数并代表了何种意义。

我们再回到这个AB规则的讨论上，你可能会问：“为什么这些演变规则、参数一定要是你说的这个样子呢？”当然，完全可以不是我说的这个样子，你完全可以自己去定义母序列以及演变规则，也可以自己去定义A和B所代表的旋转的角度，只不过如果按我上面的参数去画图的话，会生成比较有名的科赫曲线。

 

         2．F规则生成L-System分形

         前面所说的AB规则固然能生成比较多的L-System的分形，比如还能够生成科赫雪花，对应的母序列是BBB，A的演变规则为AABA，B的演变规则为BABA，但其结构一般都比较简单，尽管有的时候看起来并不简单。

比如下图所示这个L-System分形，用AB规则就无能为力了，这时我们引入L-System的比较标准的一套规则，即我所谓的F规则。F规则将AB规则中的“旋转”操作和“向前画”的操作分离开来，改用3个符号F、+、-来表示一个序列。其中F就代表了“向前画”一个单位长度，+代表“向右旋转”一个角度，-代表“向左旋转”一个角度。

这样我们只要定义了母序列，以及F的演变规则，就可以像AB规则那样生成一长串的有意义的序列了。

比如前面所说的科赫曲线，实际上也可以用F规则来描述，其母序列只有一个字符F，F的演变规则为F-F+F-F，其中-代表左旋60度，+代表右旋120。其实，这只是依我的理解写出的演变规则，如果更“规矩”一点地用F规则描述的话，在序列中应该只有一个角度变量，比如为60度，那么上面F的演变规则就应该写成F-F++F-F了，其中+就变成了右旋60度。当然，如果再“规矩”一点的话，实际上+应该代表左旋，-应该代表右旋，那么上面F规则中的+和-的位置就应该互换一下。

说道这里，其实我们完全没有必要管这么多规矩，只要我们领悟到了L-System里面序列是如何变换的并且代表何种含义就够了。这里提出这些规矩，只是想使大家以后阅读相关资料时会更清晰一些，我在后文的叙述中还是会使用基于我自己的理解的描述规则。

        有了F规则之后，我们就能生成更多更有趣的L-System分形了。比如如果母序列是F+F+F+F，F的变换规则是F->F+F-F-FFF+F+F-F，我们就会得到如下图所示的叫做科赫岛(Koch Island)的一个L-System分形。可以在My L-System里面选My_F_L-System并输入相关的参数，即可看到生成的L-System分形图。

 

        但有些时候，我们貌似用现在的F规则并不能画出一些不连续的东西，比如一棵如下图所示的L-System树。原因很简单，因为按照我们上面的描述规则，“小机器人”一直是边走边画图的，而且走过的路必然是连续的，那像下图这样的不连续的树形图要怎么去画呢？难道再定义一种操作叫做“后退”？

 

这时我们可以引入F规则中的另外两个符号’[’和’]’，其中[代表把当前的状态比如现在的位置以及所处的角度都“存”起来，什么时候再“取”出来呢？遇到]的时候就把前面保存的各种状态“取”出来，相当于恢复到了遇到[之前的状态。至于如何实现“存”和“取”的操作，我们要用栈来实现。

有了[、]这两个操作就相当于实现了“后退”的操作，这样我们就可以去画不连续的分形图了，只要在走“岔路”之前把当前的各个状态保存起来，等需要的时候再恢复就好了，恢复之后就相当于又回到了“岔路口”，这样再走另一个“岔路”即可。

比如上面那幅图所示的树，其母序列可以看做只有一个字符F，而F的演变规则为F->F[-F][+F]，其中-代表左旋45度，+代表右旋30度。同时，为了保证图像的美观程度，我们在画这幅分形图的时候需要改变每步所走的长度d的大小，具体的规则就是依“深度”来定，每增加一个“深度”，d就变为原来的60%，这一点从图形上可以直观的看出来。

        3．XYF规则生成L-System分形

有些更为复杂的L-System分形单用F规则也是没有办法构造出来的，就好比自然界中的植物一样，如果只按一个规则去生长的话，是没有办法长出那么千奇百怪的形状的。而之所以植物会这样形态各异，一定离不开一个重要的因素——变异。

借用变异的思想，我们在F表达式演变的过程中，不妨引入辅助的演变的参数及对应的规则，这样就形成了XYF规则。当然，XYF规则并不代表辅助的参数只有X、Y，实际上也可以只有他们其中之一，也可以有更多的参数，比如W、V、U、Z等等。

举个例子，比如现在只有X一个辅助参数，我们定义母序列为X，F的演变规则为F->FF，X的演变规则为X->F[[X]+X]+F[+FX]-X，其中-代表左旋23度，+代表右旋23度，这样我们就可以得到下面这样一棵树。可以在My L-System里选My_XYL_L-System并输出相关参数后，即可看到生成的L-System分形图。

 

 三、用代码实现L-System规则并画出分形

其实有了前面的理论基础之后，我们编写代码的思路就变的很清晰了。我们只要根据当前用户选定的参数计算出在当前精细程度下的表示分形的序列，并且将序列翻译成实际的意义以恰当的画线长度在恰当的地方将分形图一条线一条线地画出来即可。那么对于画出分形而言要解决的问题总的来说也就下面几点：

        1．根据母序列及演变规则，生成指定精细程度下的序列。

        2．确定画图的起始角度。

        3．确定画图的起始位置。

        4．确定画图线段的单位长度。

        至于生成序列，我们只要不停地扫描当前序列，并把特定的字符按规则演变成字符串后，添加到新序列的后面即可，这样反复操作直到达到了指定深度。值得一提的是，我一开始是用String来实现序列的生成工作的，后来发现其效率实在太低了，于是就改用了int数组来实现，这时只要将不同的字符赋予一定的整数值即可。

        至于画图的起始角度，对于大多数分形图来讲是无关紧要的，因为只不过是图进行了一定程度上的旋转而已。但对于具有特定意义的图，我们还是要按需进行设定，比如如果你要画一棵树，至少得让它往上长吧？

        至于画图的起始位置以及起始的画线的单位长度，我们可以根据生成好的序列，先假定一个步长，且假定在(0，0)这个位置出发，然后模拟一遍画图的过程（但并不进行画线的操作），观察生成的图所占的矩阵的大小，并以此为依据，来计算缩放比例以使分形图能以恰当的大小显示在恰当的位置。与此同时，我们便可以计算出起始位置以及起始的画线的单位长度了。具体的计算公式还是留给大家来思考吧，在此就不贴代码了。

 

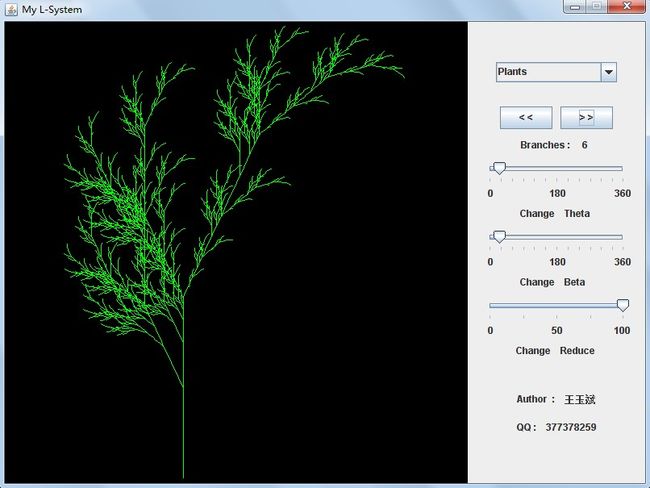
        四、My L-System的一些使用贴士

My L-System的主体由两部分组成，一部分负责显示L-System分形图，另一部分负责控制分形图的一些参数。

在下图所示的右边的控制面板上，第一行的位置可以选择L-System分形图的种类，第二行的两个按钮可以调节分形图的精细成图。在画块区域，Change Theta代表改变左旋角度的度数，也就是上文提到的-所代表的旋转角度，Change Beta代表改变右旋角度，也就是上文提到的+所代表的旋转角度，Change Reduce代表分形图没递增一个深度，画线长度变为原来的百分之多少。

 

 

        在可以自定义的L-System中，比如我们以My_XYF_L-System为例，弹出的窗体如下图所示。

 

 

我们只要依次填入代表前面所说的各个参数的值即可，值得一提的是，如果当前没有X的演变规则，或者演变的序列中根本没有X，我们在X的演变规则一栏可以直接填X，对于F和Y也是如此，直接填其本身即可。

另外附上继续附上前面提过的那个网站，在这个网站上，当你点开L-System可以表示的分形时，都会附带其演变的规则，你可以将这些演变规则填入到指定的选项里，并观察生成的图形是否和其实例的图形保持一致。

http://paulbourke.net/fractals/

当然，你也可以借助这个软件，充分发挥自己的想象，指定演变规则，并观察生成的L-System分形的具体形状，看看你创造出来的分形是不是颇富魅力呢？

P.S. 由于分形有烦有简，如果自定义的分形过于复杂，则在其生成过程中有可能出现数组越界的情况。同时，如果用户输入的表达式不合法，也可能出现未知的错误。