算法学习记录-排序——快速排序
快速排序
快速排序由图灵奖获得者Tony Hoare26岁设计出来,这个大牛有兴趣的可以google下。
前面讲过 直接插入排序、简单选择排序、冒泡排序 这几个我们能够最直接想出来的排序方法。(时间复杂度都是 O(N2))
后来人们一直寻找能够打破时间复杂度O(N2)的限制。
先后有 希尔排序,它是直接插入排序的升级。(每趟插入的步长从大到小)
堆排序,它是简单选择排序的升级。(应用堆这个结构来存储数据的大小关系)
而快速排序则是冒泡排序的升级。(冒泡排序是比较两个相邻的数大小,交换)
快速排序:
基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,
其中一部分的所有数据都比另外一部分的所有数据都要小,
然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
看完了有没有看懂?或者有没感觉到它确实比其他算法快?
1.通过一趟排序,将待排的数据分成两个部分。保证前一部分比后一部分都要小。
2.然后对这分出来的 两部分 进行同样的操作。(这里就有一个递归额思想)
严蔚敏书上对一次快速排序定义
假设待排的序列{r1,r2,r3,rn},首先任意选取一个记录(通常可选择第一个记录r1)作为枢轴(pivot),
然后按下述原则重新排列其余记录:
将所有关键字较pivot的记录小的安置在它的前面,
将所有关键字教pivot的记录大的安置在它的后面。之后,可以将该piovt记录最后的位置i作为分界线,
最后这个序列就变成了 {{r1,r2...ri-1}{ri}{ri+1,ri+2...rn}};
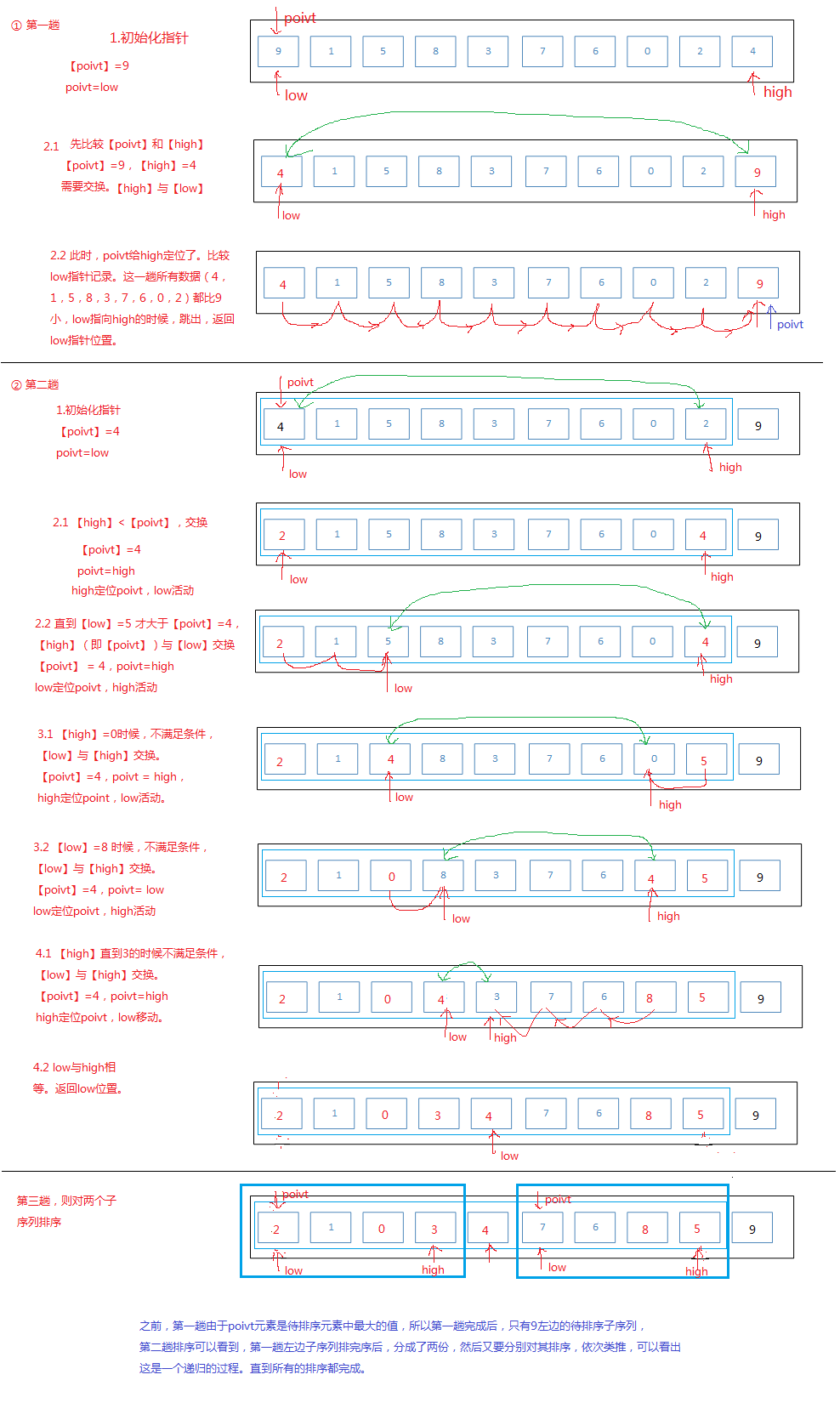
具体piovt是怎么操作的,我们看下面的图:
算法:
1.初始化的时候,pivot和low指向同一个记录。low定位了poivt,high指针活动。
2.high初试指向最末尾一个记录,比较high指针的记录是否不小于poivt记录,若不小于,则high指针就减少一个,指向前一个记录,再次与poivt比较,直到有一个记录小于poivt的记录,这个时候就交换low和high的记录数。(也是poivt与high交换),同时high就定位poivt,low开始活动。
3.同理,low与poivt(也就是high指向的记录)比较,若low不大于poivt记录,则low就指向后一个元素,直到有一个记录大于poivt,则交换low和high(poivt)的记录,同时poivt又由low定位了。
4.依次类推,直到low不小于high,返回low的值,这个就是我们划分的位置
程序:
1 //***********************quickSort*******************************// 2 3 int getpiovtPos(myDataType *ary,int low,int high) 4 { 5 int poivtVal = ary[low]; 6 myDataType temp; 7 8 while(low < high) 9 { 10 while(low < high && ary[high] >= poivtVal) 11 { 12 high--; 13 } 14 //交换 15 temp = ary[low]; 16 ary[low] = ary[high]; 17 ary[high]=temp; 18 19 while(low < high && ary[low] <= poivtVal) 20 { 21 low++; 22 } 23 //交换 24 temp = ary[low]; 25 ary[low] = ary[high]; 26 ary[high]=temp; 27 } 28 return low; 29 } 30 void QSort(myDataType *ary,int low,int high) 31 { 32 int poivt; 33 if (low < high) 34 { 35 poivt = getpiovtPos(ary,low,high); 36 37 QSort(ary,low,poivt-1); 38 QSort(ary,poivt+1,high); 39 } 40 } 41 void quickSort(myDataType *ary,int len) 42 { 43 QSort(ary,0,len-1); 44 }
完整代码:
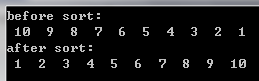
1 typedef int myDataType; 2 //myDataType src_ary[10] = {9,1,5,8,3,7,6,0,2,4}; 3 //myDataType src_ary[10] = {1,2,3,4,5,6,7,8,9,10}; 4 myDataType src_ary[10] = {10,9,8,7,6,5,4,3,2,1}; 5 void prt_ary(myDataType *ary,int len) 6 { 7 int i=0; 8 while(i < len) 9 { 10 printf(" %d ",ary[i++]); 11 } 12 printf("\n"); 13 } 14 //***********************quickSort*******************************// 15 16 int getpiovtPos(myDataType *ary,int low,int high) 17 { 18 int poivtVal = ary[low]; 19 myDataType temp; 20 21 while(low < high) 22 { 23 while(low < high && ary[high] >= poivtVal) 24 { 25 high--; 26 } 27 //交换 28 temp = ary[low]; 29 ary[low] = ary[high]; 30 ary[high]=temp; 31 32 while(low < high && ary[low] <= poivtVal) 33 { 34 low++; 35 } 36 //交换 37 temp = ary[low]; 38 ary[low] = ary[high]; 39 ary[high]=temp; 40 } 41 return low; 42 } 43 void QSort(myDataType *ary,int low,int high) 44 { 45 int poivt; 46 if (low < high) 47 { 48 poivt = getpiovtPos(ary,low,high); 49 50 QSort(ary,low,poivt-1); 51 QSort(ary,poivt+1,high); 52 } 53 } 54 void quickSort(myDataType *ary,int len) 55 { 56 QSort(ary,0,len-1); 57 } 58 int _tmain(int argc, _TCHAR* argv[]) 59 { 60 printf("before sort:\n"); 61 prt_ary(src_ary,10); 62 63 quickSort(src_ary,10); 64 65 printf("after sort:\n"); 66 prt_ary(src_ary,10); 67 68 69 70 getchar(); 71 return 0; 72 }
测试结果:
冒泡排序中,优化其算法的时候,只有有一次没有元素移动,就可以判断排序完成,减少了不必要的比较,提高了时间效率。
快速排序的优化可以从这些方面入手,
在getpiovtPos函数中,可以不需要交换,直接将最后的结果赋给最后的需要交换的那个元素就可以了。比如上图中,第二趟poivt元素4,经过了
多次交换位置(绿色的箭头),最后到达它应该的位置。
1 int getpiovtPos_opt(myDataType *ary,int low,int high) 2 { 3 int poivtVal = ary[low]; 4 while(low < high) 5 { 6 while(low < high && ary[high] >= poivtVal) 7 { 8 high--; 9 } 10 //覆盖 11 ary[low] = ary[high]; 12 13 while(low < high && ary[low] <= poivtVal) 14 { 15 low++; 16 } 17 //覆盖 18 ary[high] = ary[low]; 19 } 20 ary[low] = poivtVal; 21 return low; 22 }
补充:
假设,每次取poivt元素都是待排元素最大的元素,那么这就是该排序最差的效率。
能不能通过改进,通过一种方法,能够避免这样的情况?
比如掷硬币,得到正面的概率永远是1/2,那么我们也能够增加一个随机数,能够使得poivt的值都是随机的,这样就能够避免人为的取得较差的效率。