尼姆博弈(Nimm's Game)
尼姆博弈(Nimm's Game)
题型
尼姆博弈模型,大致上是这样的:
有3堆各若干个物品,两个人轮流从某一堆取任意多的物品,规定每次至少取1个,多者不限,最后取光者得胜。
分析
1、首先自己想一下,就会发现只要最后剩两堆物品一样多(不为零),第三堆为零,那面对这种局势的一方就必败
那我们用(a,b,c)表示某种局势,首先(0,0,0)显然是必败态,无论谁面对(0,0,0) ,都必然失败;第二种必败态是(0,n,n),自己在某一堆拿走k(k ≤ n)个物品,不论k为多少,对方只要在另一堆拿走k个物品,最后自己都将面临(0,0,0)的局势,必败。仔细分析一下,(1,2,3)也是必败态,无论自己如何拿,接下来对手都可以把局势变为(0,n,n)的情形
那这种奇异局势有什么特点呢?
也不知谁这么牛逼,竟然能把这种局势和二进制联系在一起
这里说一种运算符号,
异或'^',a^b=a'b+ab'(a'为非a)
我们用符号XOR表示这种运算,这种运算和一般加法不同的一点是1 XOR 1 = 0。先看(1,2,3)的按位模2加的结果:
1 = 二进制01
2 = 二进制10
3 = 二进制11 XOR
———————
0 = 二进制00 (注意不进位)
对于奇异局势(0,n,n)也一样,结果也是0
任何奇异局势(a,b,c)都有a XOR b XOR c = 0
如果我们面对的是一个非必败态(a,b,c),要如何变为必败态呢?
假设 a < b < c,我们只要将 c 变为a XOR b,即可。因为有如下的运算结果:
a XOR b XOR (a XOR b)=(a XOR a) XOR (b XOR b) = 0 XOR 0 = 0
要将c 变为a XOR b,只要对 c进行 c-(a XOR b)这样的运算即可
2、尼姆博弈模型可以推广到:有n堆若干个物品,两个人轮流从某一堆取任意多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
这个游戏中的变量是堆数k和各堆的物品数N1,N2,……,Nk。
对应的组合问题是,确定先手获胜还是后手获胜以及两个游戏人应该如何取物品才能保证自己获胜
3、为了进一步理解Nim取物品游戏,我们看看特殊情况。
如果游戏开始时只有一堆物品,先手则通过取走所有的物品而获胜。现在设有2堆物品,且物品数量分别为N1和N2。游戏者取得胜利并不在于N1和N2的值具体是多少,而是取决于它们是否相等。
也就说两堆的策略我们有了,现在我们如何从两堆的取子策略扩展到任意堆数中呢?
首先回忆一下,每个正整数都有对应的一个二进制数,例如:57(10) = 111001(2) ,即:57(10)=25+24+23+20。于是,我们可以认为每一堆物品数由2的幂数的子堆组成。这样,含有57枚物品大堆就能看成是分别由数量为25、24、23、20的各个子堆组成
现在考虑各大堆大小分别为N1,N2,……Nk的一般的Nim博弈。将每一个数Ni表示为其二进制数(数的位数相等,不等时在前面补0):
N1 = as…a1a0
N2 = bs…b1b0
……
Nk = ms…m1m0
如果每一种大小的子堆的个数都是偶数,我们就称Nim博弈是平衡的,而对应位相加是偶数的称为平衡位,否则称为非平衡位。因此,Nim博弈是平衡的,当且仅当:
as +bs + … + ms 是偶数,即as XOR bs XOR … XOR ms = 0
……
a1 +b1 + … + m1 是偶数,即a1 XOR b1 XOR … XOR m1 = 0
a0 +b0 + … + m0是偶数,即a0 XOR b0 XOR … XOR m0 = 0
于是,我们就能得出尼姆博弈中先手获胜策略:
Bouton
定理:
先手能够在非平衡尼姆博弈中取胜,而后手能够在平衡的尼姆博弈中取胜。即状态(x1, x2, x3, …, xn)为P状态当且仅当x1 xor x2 xor x3 xor … xor xn =0。这样的操作也称为Nim和(Nim Sum)
我们以一个两堆物品的尼姆博弈作为试验。设游戏开始时游戏处于非平衡状态。这样,先手就能通过一种取子方式使得他取子后留给后手的是一个平衡状态下的游戏,接着无论后手如何取子,再留给先手的一定是一个非平衡状态游戏,如此反复进行,当后手在最后一次平衡状态下取子后,先手便能一次性取走所有的物品而获胜。而如果游戏开始时游戏牌平衡状态,那根据上述方式取子,最终后手能获
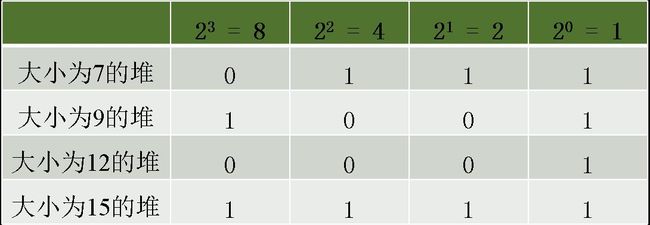
下面应用此获胜策略来考虑4堆的Nim博弈。其中各堆的大小分别为7,9,12,15枚硬币。用二进制表示各数分别为:0111,1001,1100和1111
于是可得到如下一表:
由Nim博弈的平衡条件可知,此游戏是一个非平衡状态的Nim博弈,因此,先手在按获胜策略一定能够取得最终的胜利。具体做法有多种,先手可以从大小为12的堆中取走11枚硬币,使得游戏达到平衡(如下表)
之后,无论后手如何取子,先手在取子后仍使得游戏达到平衡
同样的道理,先手也可以选择大小为9的堆并取走5枚硬币而剩下4枚,或者,先手从大小为15的堆中取走13枚而留下2枚
归根结底, Nim博弈的关键在于游戏开始时游戏处于何种状态(平衡或非平衡)和先手是否能够按照取子游戏的获胜策略来进行游戏
当堆数大于2时,我们看出Bouton定理依旧适用,下面用数学归纳法证明
证明:如果每堆都为0,显然是P状态(必败)。下面验证P状态和N状态的后两个递推关系:
一、每个N状态都可以一步到达P状态。
证明是构造性的。检查Nim和X的二进制表示中最左边一个1,则随便挑一个该位为1的物品堆Y,根据Nim和进行调整(0变1,1变0)即可。例如Nim和为100101011,而其中有一堆为101110001。为了让Nim和变为0,只需要让操作的物品数取操作前的物品数和Nim的异或即可
显然操作后物品数变小,因此和合法的。设操作前其他堆的Nim和为Z,则有Y xor Z = X。操作后的Nim和为X xor Y xor Z = X xor X = 0,是一个P状态
二、每个P状态(必胜态)都不可以一步到达P状态
由于只能改变一堆的物品,不管修改它的哪一位,Nim的对应位一定不为0,不可能是P状态。
这样就证明了Bouton定理
实际解决
Nim博弈中如果规定最后取光者输,情况是怎样的?
初看起来问题要复杂很多(因为不能主动拿了,而要“躲着”拿,以免拿到最后一个物品),但对于Nim游戏来说,几乎是一样的:
首先按照普通规则一样的策略进行,直到恰好有一个物品数大于1的堆x。在这样的情况下,只需要把堆x中的物品拿得只剩1个物品或者拿完,让对手面临奇数堆物品,这奇数堆物品每堆恰好1个物品。这样的状态显然是必败的。由于你每次操作后需要保证Nim和为0,因此不可能在你操作后首次出现“恰好有一个物品数大于1的堆”。新游戏得到了完美解决
Being a Good Boy in Spring Festival
Problem Description
一年在外 父母时刻牵挂
春节回家 你能做几天好孩子吗
寒假里尝试做做下面的事情吧
陪妈妈逛一次菜场
悄悄给爸爸买个小礼物
主动地 强烈地 要求洗一次碗
某一天早起 给爸妈用心地做回早餐
如果愿意 你还可以和爸妈说
咱们玩个小游戏吧 ACM课上学的呢~
下面是一个二人小游戏:桌子上有M堆扑克牌;每堆牌的数量分别为Ni(i=1…M);两人轮流进行;每走一步可以任意选择一堆并取走其中的任意张牌;桌子上的扑克全部取光,则游戏结束;最后一次取牌的人为胜者。
现在我们不想研究到底先手为胜还是为负,我只想问大家:
——“先手的人如果想赢,第一步有几种选择呢?”
春节回家 你能做几天好孩子吗
寒假里尝试做做下面的事情吧
陪妈妈逛一次菜场
悄悄给爸爸买个小礼物
主动地 强烈地 要求洗一次碗
某一天早起 给爸妈用心地做回早餐
如果愿意 你还可以和爸妈说
咱们玩个小游戏吧 ACM课上学的呢~
下面是一个二人小游戏:桌子上有M堆扑克牌;每堆牌的数量分别为Ni(i=1…M);两人轮流进行;每走一步可以任意选择一堆并取走其中的任意张牌;桌子上的扑克全部取光,则游戏结束;最后一次取牌的人为胜者。
现在我们不想研究到底先手为胜还是为负,我只想问大家:
——“先手的人如果想赢,第一步有几种选择呢?”
Input
输入数据包含多个测试用例,每个测试用例占2行,首先一行包含一个整数M(1<M<=100),表示扑克牌的堆数,紧接着一行包含M个整数Ni(1<=Ni<=1000000,i=1…M),分别表示M堆扑克的数量。M为0则表示输入数据的结束。
Output
如果先手的人能赢,请输出他第一步可行的方案数,否则请输出0,每个实例的输出占一行。
Sample Input
3
5 7 9
0
Sample Output
1
分析:由上分析第1点可知,只要对 c进行 c-(a XOR b)这样的运算即可
代码如下:
# include<stdio.h> int main() { int nPile,i,sum,cnt; int p[105]; while(scanf("%d",&nPile)&&nPile) { cnt=0; sum=0; for(i=0;i<nPile;i++) { scanf("%d",&p[i]); sum^= p[i]; } for(i=0;i<nPile;i++) { if(p[i]>(sum^p[i]))//注意'^'的优先级小于'>' cnt++; } printf("%d\n",cnt); } return 0; }