概率图模型（PGM）学习笔记（三）模式判断与概率图流

我们依旧使用“学生网络”作为样例，如图1。

 

图1

首先给出因果判断（Causal Reasoning）的直觉解释。

能够算出来

即学生获得好的推荐信的概率大约是0.5.

但假设我们知道了学生的智商比較低，那么拿到好推荐信的概率就下降了：

进一步，假设又同一时候知道了考试的难度非常低，那么他拿到好的推荐信得概率又上升了，甚至还能超过最初的概率：

上述这个过程就是因果判断，你看它是顺着箭头的方向进行判断。

 

其次给出信度判断（Evidential Reasoning）的直觉解释。如图2.

图2

本来已知考试难度高和学生非常聪明的概率分别为0.4和0.3

如今我们忽然知道这个悲剧的同学考试里得了C等。

那么如今考试难度高的概率就上升了，学生非常聪明的概率就下降了：

上述这个过程就是信度判断，你看它是逆着箭头方向进行判断的。

 

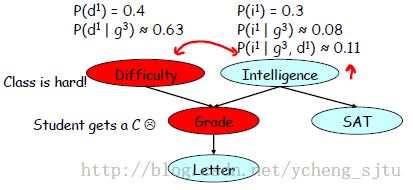
再次给出交叉因果判断（Intercausal Reasoning）的直觉解释，如图3.

图3

信度判断指出，在已知该同学考了C等之后，他非常聪明的概率下降到0.08了，

假设此时我们又知道这次考试非常难，那么他非常聪明的概率会有一个轻微的上升，到0.11：

交叉因果判断的特点是Difficulty顺着箭头到了Grade，又逆着箭头影响到了Intelligence.

 

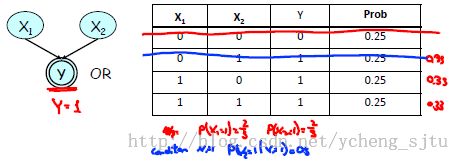
为什么会这样？我们考虑一个最简单的情况，如图4.

图4

一開始能够看到，X1和X2是全然独立的，同一时候有若已知Y=1

然而，当我们已知X1=1之后，X2=1的概率下降了：

 

再来看看这个同学考了B是什么效果，如图5.

图5

本来学生非常聪明的概率是0.3，后来知道了他考了B，那么他非常聪明的概率下降到了0.175.

如今又知道了，这门考试事实上蛮难的。那么他非常聪明的概率又上升到了0.34，竟然超过了原始的0.3.

 

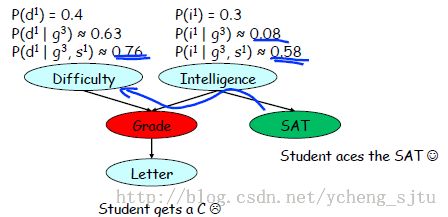
如今再考虑一个情况：这个同学在SAT測验中得了A，如图6.

图6

这对考试非常难以及学生非常聪明的概率有什么影响吗？回到那位考了C的悲剧同学。

这个同学考了C，所以考试非常难的概率为0.63，学生非常聪明的概率降到0.08

如今，忽然又知道了这个同学蛮厉害的，在SAT中考了A

于是，考试非常难的概率达到了0.76，学生非常聪明的概率达到了0.58，两者都大大超过了他们本来的概率。这是由于，同学的SAT成绩为A改变了我们对其智商的认识，从而影响到了在他考了C时，对其考试难度的认识。

 

通过上述直观分析，我们发现概率图中的节点是可以相互影响的，以下做详细分析。如图7.

图7

设随机变量X和Y，在什么情况下是能够相互影响的呢？

1.X与Y直接相连时他们能够相互影响。

比方告诉你考试非常easy，那么你得分高的概率自然上升。告诉你得了C，那么考试非常easy的概率就会下降。

 

2.X与Y中间隔了一个W，在连接箭头方向不变的情况下，X与Y可以相互影响。

比方告诉你这个同学得到了一封不错的推荐信，那么考试简单的概率就上升了。告诉你考试难度非常大，那么他能得到好推荐信的概率就下降了。

 

3.X与Y之间隔了一个W，假设当中箭头是指向外的方向，X与Y可以相互影响。

比方同学的SAT成绩显然和他的Grade是相互影响的。这就像一个人每次模拟考试都能拿高分，我们自然有理由相信他能力非常强，足以在高考中获得好成绩。

 

4.X与Y之间隔了一个W，假设当中箭头是指向内的方向，那么X与Y就不能相互影响了。

比方告诉你考试非常难，但这跟同学的智商有什么关系呢？反之亦然。

 

总之，假设一条关系链中没有形如的结构，那么这条关系链就能把影响传递下去。

 

以上讨论的都是我们对中间环节W一无所知的情况。

假设我们知道关于中间环节W的信息呢，X与Y之间的相互影响是否会因此而发生改变呢？我们用Z集合表示我们知道相关信息的意思。如图8.

图8

分栏左側就是我们上面讨论的情况：我们对W一无所知。

右边栏是指我们已经知道W的概率了。再来观測X与Y之间的影响。

 

奇妙的事情出现了：假设我们知道了W的概率，会把之前通畅的关系链给打断了；而把之前阻塞的关系链打通了。

详细地：同学SAT得了A，可是我们已知这个同学智商事实上超级笨，那么他考试拿高分的概率会由于他SAT的狗屎运而增多吗？不会的，依据定义，考试成绩仅仅与他的智商和考试难度有关，跟他碰巧考好的SAT没有不论什么关系。由于我们已经知道他实际上非常笨了，SAT只是是个意外。

而之前阻塞的链接如今却通了。比方说考试非常难，这和同学智商没有不论什么关系，可是假设我知道了考试非常难，同学考了A，那么我们非常有理由相信，同学应该非常聪明啦。

 

这张图中，S-I-G-D这条路径在I不知道、G知道的情况下才干通畅无阻。

 

Tips：事实上这个结论还应该扩展一下。

已知试卷非常难，不知道考了多少分，可是我们知道这个同学利用这个分数拿到了一封非常好的推荐信，我们就有理由相信，他应该考得不错，进而相信他应该是个挺聪明的童鞋。

 

总之。假设一条关系链中在每一个形如的结构里，我们知道Xi或者至少知道他的某一个子节点的概率（就像我们尽管不知道Grade，可是我们知道了Letter的概率），那么这条关系链就能把影响传递下去。

 

独立性

独立性的定义能够有下面3种描写叙述：

 

类似地，条件独立也能够这么写

 

以下直观感受一下条件独立性，如图9

图9

有2枚硬币，一仅仅均匀，还有一仅仅不均匀并且又90%的概率能正面朝上。当然，两枚硬币外观是全然一样的。

 

如今让你抽出一枚，准备扔2次。

你先扔了第一次，发现正面朝上，那么能够相信，第二次还是正面朝上的概率肯定添加了，这样第二次投硬币的结果受到了第一次投硬币的影响。

而我如今告诉你事实上你刚刚投的是均匀硬币（或者不均匀，无所谓的），那么你第二次投硬币的概率和第一次投出来的结果就失去了联系。

这就说明了条件有时会使变量之间的相关性丧失。

欢迎參与讨论并关注本博客和微博以及知乎个人主页，兴许内容继续更新哦~

转载请您尊重作者的劳动，完整保留上述文字以及本文链接，谢谢您的支持！