yaoqiang2011

NLP系列(5)_从朴素贝叶斯到N-gram语言模型

作者：龙心尘 && 寒小阳
时间：2016年2月。
出处：http://blog.csdn.net/longxinchen_ml/article/details/50646528
http://blog.csdn.net/han_xiaoyang/article/details/50646667
声明：版权所有，转载请联系作者并注明出处

1. 引言：朴素贝叶斯的局限性

我们在之前文章《NLP系列(2)_用朴素贝叶斯进行文本分类(上)》探讨过，朴素贝叶斯的局限性来源于其条件独立假设，它将文本看成是词袋子模型，不考虑词语之间的顺序信息，就会把“武松打死了老虎”与“老虎打死了武松”认作是一个意思。那么有没有一种方法提高其对词语顺序的识别能力呢？有，就是本节要接到的N-gram语言模型。

2. N-gram语言模型是啥？

2.1从假设性独立到联合概率链规则

照抄我们前文垃圾邮件识别中的条件独立假设，长这个样子：

P(（“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)|S)
=P(“我”|S)×P(“司”|S)×P(“可”|S)×P(“办理”|S)×P(“正规发票”|S)
×P(“保真”|S)×P(“增值税”|S)×P(“发票”|S)×P(“点数”|S)×P(“优惠”|S)

为了简化起见，我们以字母 xi 表示每一个词语，并且先不考虑条件“S”。于是上式就变成了下面的独立性公式。

P(x1,x2,x3,x4,x5,x6,x7,x8,x9,x10)
=P(x1)P(x2)P(x3)P(x4)P(x5)P(x6)P(x7)P(x8)P(x9)P(x10)
=P(“我”)P(“司”)P(“可”)P(“办理”)...P(“优惠”)

如果不满足独立性假设，上面的等号就不成立。 那么有没有一个不依赖于任何其他的假设，而能够原原本本地把所有的语序信息都考虑进来的恒等式呢？有，它就是联合概率链规则(chain rule) ：

P(x1,x2,x3,x4,x5,…,xn)
=P(x1)P(x2|x1)P(x3|x1,x2)...P(xn|x1,x2,...,xn−1)

2.2 从联合概率链规则到n-gram语言模型

上面的联合概率链规则公式虽然考虑到了所有的词和词之间的依赖关系，但是非常复杂，在实际生活中几乎没办法使用，于是我们就想了很多办法去近似这个公式，效果又要求比独立性假设好。比如我们要讲到的语言模型n-gram就是一个这样的简化。

如果我们考虑一个词语对上一个词语的依赖关系，公式就简化成了如下形式，我们把它叫做二元语法（bigram，2-gram）:

P(x1,x2,x3,x4,x5,x6,x7,x8,x9,x10)
=P(x1)P(x2|x1)P(x3|x2)P(x4|x3)..P(x10|x9)
=P(“我”)P(“司”|“我”)P(“可”|“司”)P(“办理”|“可”)...P(“优惠”|“点数”)

如果把依赖词长度再拉长一点，考虑一个词对前两个词的依赖关系，就叫做三元语法（trigram，3-gram），公式如下:

P(x1,x2,x3,x4,x5,x6,x7,x8,x9,x10)
=P(x1)P(x2|x1)P(x3|x1,x2)P(x4|x2,x3)×...×P(x10|x8,x9)
=P(“我”)P(“司”|“我”)P(“可”|“我”,“司”)P(“办理”|“司”,“可”)...P(“优惠”|“发票”,“点数”)

如果我们再考虑长一点，考虑n个词语之间的关系，恩恩，这就是n-gram的由来。歪果仁果然取名字简单粗暴又好记…

其实以上几个简化后的公式，就是著名的马尔科夫假设（Markov Assumption）：下一个词的出现仅依赖于它前面的一个或几个词。这相对于联合概率链规则，其实是一个有点粗糙的简化，不过很好地体现了就近思路，离得较远和关系比较弱的词语就被简化和省略了。实际应用中，这些简化后的n-gram语法比独立性假设还是强很多的。其实可以把独立性假设理解成为1-gram。

2.3 怎样选择依赖词的个数“n”？

选择依赖词的个数“n”主要与计算条件概率有关。理论上，只要有足够大的语料，n越大越好，毕竟这样考虑的信息更多嘛。条件概率很好算，统计一下各个元组出现的次数就可以，比如:

P(“优惠”|“发票”,“点数”)=(“发票”,“点数”，“优惠”)出现的次数(“发票”,“点数”)出现的次数

但我们实际情况往往是训练语料很有限，很容易产生数据稀疏，不满足大数定律，算出来的概率失真。比如(“发票”,“点数”，“优惠”)在训练集中竟没有出现，就会导致零概率问题。

又比如在英文语料库IBM, Brown中，三四百兆的语料，其测试语料14.7%的trigram和2.2%的bigram在训练语料中竟未出现！

另一方面，如果n很大，参数空间过大，产生维数灾难，也无法实用。假设词表的大小为 100,000 ，那么n-gram模型的参数数量为 100,000n 。这么多的参数，估计内存就不够放了。

那么，如何选择依赖词的个数n呢？从前人的经验来看：

经验上，trigram用的最多。尽管如此，原则上，能用bigram解决，绝不使用trigram。n取≥4的情况较少。
当ｎ更大时：对下一个词出现的约束信息更多，具有更大的辨别力；
当ｎ更小时：在训练语料库中出现的次数更多，具有更可靠的统计信息，具有更高的可靠性、实用性。

3. N-gram实际应用举例

说了这么N-gram语言模型的背景知识，咱们再来看看N-gram语言模型在自然语言处理中有哪些常见应用。

PS：此部分以原理介绍为多，具体的技术实现细节请参考文中链接或者google。

3.1 词性标注

词性标注是一个典型的多分类问题。常见的词性包括名词、动词、形容词、副词等。而一个词可能属于多种词性。如“爱”，可能是动词，可能是形容词，也可能是名词。但是一般来说，“爱”作为动词还是比较常见的。所以可以统一给“爱”分配为“动词”。这种最简单粗暴的思想非常好实现，如果准确率要求不高则也比较常用。它只需要基于词性标注语料库做一个统计就够了，连贝叶斯方法、最大似然法都不要用。词性标注语料库一般是由专业人员搜集好了的，长下面这个样子。其中斜线后面的字母表示一种词性，词性越多说明语料库分得越细：

需要比较以下各概率的大小，选择概率最大的词性即可：

P(词性i|“爱")=“爱"作为“词性i”的次数“爱"出现的次数；i=1,2,3...

但这种方法没有考虑上下文的信息。而一般来说，形容词后面接名词居多，而不接动词，副词后面才接动词，而不接名词。 考虑到词性会受前面一两个词的词性的影响，可以引入2-gram模型提升匹配的精确度。 我们匹配以下这句话（已被空格分好词）中“爱”的词性：

“闷骚的李雷很爱韩梅梅”

将公式进行以下改造，比较各概率的大小，选择概率最大的词性：

P(词性i|“很”的词性（副词），“爱")=前面被“副词”修饰的“爱"作为“词性i”的次数前面被“副词”修饰的“爱"出现的次数；i=1,2,3...

计算这个概率需要对语料库进行统计。但前提是你得先判断好“很”的词性，因为采用2-gram模型，进而就需要提前判断“李雷”的词性，需要判断“闷骚的”词性。但是“闷骚的”作为第一个词语，已经找不比它更靠前的词语了。这时就可以考虑用之前最简单粗暴的方法判断“闷骚的”的词性，统一判断为形容词即可。

PS:词性标注是自然语言处理中的一项基础性工作，有其细节实现远比我们介绍地更加丰富。感兴趣的同学可以看看这篇文章《NLTK读书笔记 — 分类与标注》

3.2 垃圾邮件识别

是的，亲，你！没！看！错！可以用N-gram进行垃圾邮件识别，而且是朴素贝叶斯方法的进化版。下面我们用直观的例子探讨一下其在分类问题上是怎么发挥作用的。一个可行的思路如下：

先对邮件文本进行断句，以句尾标点符号（“。” “!” “？”等）为分隔符将邮件内容拆分成不同的句子。
用N-gram分类器(马上提到)判断每个句子是否为垃圾邮件中的敏感句子。
当被判断为敏感句子的数量超过一定数量（比如3个）的时候，认为整个邮件就是垃圾邮件。

咳咳，有同学问N-gram分类器是什么鬼，这个分类器靠谱么。N-gram分类器是结合贝叶斯方法和语言模型的分类器。这里用 Y1,Y2 分别表示这垃圾邮件和正常邮件，用 X 表示被判断的邮件的句子。根据贝叶斯公式有：

P(Yi|X)∝P(X|Yi)P(Yi)；i=1,2

比较i=1和2时两个概率值的大小即可得到 X 所属的分类。对于句子（“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)用字母 X 代表，每一个词语用字母 xi 表示。 X 就可以写成一个 xi 组成的向量， xi 就是这向量中某个维度的特征。对 P(X|Yi) 套用2-gram模型。 则上式化简为：

P(Yi|X)∝P(X|Yi)P(Yi)；i=1,2
∝P(x1|Yi)P(x2|x1，Yi)P(x3|x2，Yi)...P(x10|x9，Yi)P(Yi)
∝P(“我”|Yi)P(“司”|“我”，Yi)P(“可”|“司”，Yi)...P(“优惠”|“点数”，Yi)P(Yi)

公式中的条件概率也比较好求，举个例子：

P(“优惠”|“点数”，Yi)=在类别Yi中，(“点数”，“优惠”)出现的次数在类别Yi中，“点数”出现的次数

剩下的就需要在语料库中间做一个的统计就是了。因为这种方法考虑到了词语前面的一个词语的信息，同时也考虑到了部分语序信息，因此区分效果会比单纯用朴素贝叶斯方法更好。

多提几句，N-gram方法在实际应用中有一些tricks需要注意：

3-gram方法的公式与上面类似。此处省略。从区分度来看，3-gram方法更好些。
句子开头的词，比如本例中的“我”，因为要考虑其本身作为开头的特征，可以考虑在其前面再添加一个句子起始符号如 “<s>” ，这样我们就不必单独计算 P(“我”|Yi) ，而是替换为计算 P(“我”|“<s>”,Yi) 。形式上与2-gram统一。这样统计和预测起来都比较方便。
一般地，如果采用N-gram模型，可以在文本开头加入n-1个虚拟的开始符号，这样在所有情况下预测下一个词的可依赖词数都是一致的。
与朴素贝叶斯方法一样，N-gram模型也会发生零概率问题，也需要平滑技术。 别着急，下面马上讨论到。

3.3 中文分词

之前说过，中文分词技术是“中文NLP中，最最最重要的技术之一”，重要到某搜索引擎厂有专门的team在集中精力优化这一项工作，重要到能影响双语翻译10%的准确度，能影响某些query下搜索引擎几分之一的广告收入。不过简单的分词实现方式中，包含的原理其实也非常易懂。

说起来，中文分词也可以理解成一个多分类的问题。 这里用 X 表示被分词的句子“我司可办理正规发票”， 用 Yi 表示该句子的一个分词方案。 咱们继续套用贝叶斯公式：

P(Yi|X)∝P(X|Yi)P(Yi)；i=1,2,3...

比较这些概率的大小，找出使得 P(Yi|X) 最大的 Yi 即可得到 X 所属的分类(分词方案)了。

Yi 作为分词方案，其实就是个词串，比如（“我司”，“可”，“办理”，“正规发票”）或者（“我”，“司可办”，“理正规”，“发票”），也就是一个向量了。

而上面贝叶斯公式中 P(X|Yi) 项的意思就是在分类方案 Yi 的前提下，其对应句子为 X 的概率。而无论分词方案是（“我司”，“可”，“办理”，“正规发票”）还是（“我”，“司可办”，“理正规”，“发票”），或者其他什么方案，其对应的句子都是“我司可办理正规发票”。也就是说任意假想的一种分词方式之下生成的句子总是唯一的（只需把分词之间的分界符号扔掉剩下的内容都一样）。于是可以将 P(X|Yi) 看作是恒等于1的。这样贝叶斯公式又进一步化简成为：

P(Yi|X)∝P(Yi)；i=1,2,3...

也就是说我们只要取最大化的 P(Yi) 就成了。而 Yi 就是一个词串，也就是一个向量，可以直接套用我们上面的N-gram语言模型。这里采用2-gram。于是有：

P(Y1)=P(“我司”，“可”，“办理”，“正规发票”)
=P(“我司”)P(“可”|“我司”)P(“办理”|“可”)P(“正规发票”|“办理”）

第二种分词方案的概率为：

P(Y2)=P(“我”，“司可办”，“理正规”，“发票”)
=P(“我”)P(“司可办”|“我”)P(“理正规”|“司可办”)P(“发票”|“理正规”）

由于在语料库中“司可办”与“理正规”一起连续出现的概率为0，于是 P(Y2)=0 , P(Y1) 的概率更高，优先选择 Y1 的分词方案。

3.4 机器翻译与语音识别

除了上述说到的应用，N-gram语言模型在机器翻译和语音识别等顶级NLP应用中也有很大的用途。

当然，机器翻译和语音识别是非常复杂的过程，N-gram语言模型只是其中的一部分，但是缺少它整个过程却进行不下去。对于这两个应用我们不打算罗列大量的公式，而只是举些例子，让大家了解一下语言模型是怎么发挥作用的。

对于机器翻译而言，比如中译英，我们对于同一句话『李雷出现在电视上』，得到的三个译文：

LiLei appeared in TV
In LiLei appeared TV
LiLei appeared on TV

其对应短语的翻译概率是一致的，从短语翻译的角度我们无法评定哪句才是正确的翻译结果。这时候，如果我们再使用语言模型(比如机器翻译里面最常见的是3-gram)，我们计算会得到最后一句话的概率：

P(“LiLei”|“<s>”,“<s>”)P(“appeared”|“LiLei”,“<s>”)P(“on”|“LiLei”,“appeared”)P(“TV”|“appeared”,“on”)

它高于第一句和第二句的概率：

P(“LiLei”|“<s>”,“<s>”)P(“appeared”|“LiLei”,“<s>”)P(“in”|“LiLei”,“appeared”)P(“TV”|“appeared”,“in”)
P(“in”|“<s>”,“<s>”)P(“LiLei”|“in”,“<s>”)P(“appeared”|“LiLei”,“in”)P(“TV”|“appeared”,“appeared”)

因此我们选择第三句作为正确的答案。这也表明大量语料上的语言模型能够在一定程度上，体现出我们表达某种语言时候的说话习惯。

对应到语音识别问题中，我们也会遇到相同的问题，对于以下的2个句子：

I went to a party
Eye went two a bar tea

或者对应下述2个句子：

你现在在干什么？
你西安载感什么？

其对应的发音是完全一致的，这时如果我们借助于语言模型，我们会算出这句话的概率：

P(“I”|“<s>”,“<s>”)P(“went”|“I”,“<s>”)P(“to”|“I”,“went”)
×P(“a”|“went”,“to”)P(“party”|“to”,“a”)

它大于:

P(“Eye”|“<s>”,“<s>”)P(“went”|“Eye”,“<s>”)P(“two”|“Eye”,“went”)
×P(“a”|“went”,“two”)P(“bar”|“two”,“a”)P(“tea”|“a”,“bar”) ，

而这句话的概率：

P(“你”|“<s>”,“<s>”)P(“现在”|“你”,“<s>”)P(“在”|“你”,“现在”)P(“干什么”|“在”,“现在”)

它远大于

P(“你”|“<s>”,“<s>”)P(“西安”|“你”,“<s>”)P(“载”|“西安”,“你”)P(“感”|“西安”,“载”)P(“什么”|“感”,“载”)

因此我们会选择I went to a party 和 你现在在干什么作为正确的语音识别结果。

上面只是简单的举例，但是大家应该看出来了，在机器翻译和语音识别中，N-gram语言模型有着至关重要的地位。同样在现在最顶级的计算机视觉任务『图片内容表述』中，语言模型也发挥着至关重要的作用。语言模型的重要性可见一斑。

4. 平滑技术

现在我们可以比较专门探讨平滑技术了。为了解决零概率问题呢，我们需要给 “未出现的n-gram条件概率分布一个非零估计值，相应得需要降低已出现n-gram条件概率分布，且经数据平滑后一定保证概率和为1”。这就是平滑技术的基本思想。

4.1 拉普拉斯平滑

这是最古老的一种平滑方法，又称加一平滑法，其保证每个n-gram在训练语料中至少出现1次。以计算概率 P(“优惠”|“发票”,“点数”) 为例，公式如下：

P(“优惠”|“发票”,“点数”)=(“发票”,“点数”，“优惠”)出现的次数+1(“发票”,“点数”)出现的次数+所有不重复的三元组的个数

在所有不重复的三元组的个数远大于(“发票”,“点数”)出现的次数时，即训练语料库中绝大部分n-gram都是未出现的情况（一般都是如此），拉普拉斯平滑有“喧宾夺主”的现象，效果不佳。

4.2 古德图灵(Good Turing)平滑

通过对语料库的统计，我们能够知道出现 r 次（r>0）的n元组的个数为 Nr 。可以令从未出现的n元组的个数为 N0 。古德图灵平滑的思想是:

出现0次的n元组也不能认为其是0次，应该给它一个比较小的估计值，比如为 d0 次。
为了保证总共的（出现和未出现的）n元组的次数不变，其他所有已出现的n元组的次数r应该打一个折扣，比如为 dr 次。
然后再用新的 dr 去计算各个条件概率。

所以问题的关键是计算 dr 。为了保证平滑前后n元组的总共出现次数不变，有：

$\sum r = 0 \infty d r \times N r = \sum r = 0 \infty (r + 1) \times N r + 1$

所以干脆令：

dr×Nr=(r+1)×Nr+1；r=0,1,2...

这样就可以求出 dr 了。但是，当 Nr>Nr+1 时，使得模型质量变差，如下图所示：

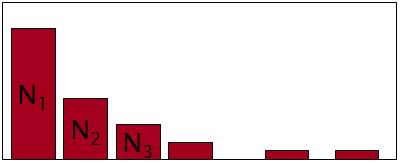
直接的改进策略就是 “对出现次数超过某个阈值的n元组，不进行平滑，阈值一般取8~10”，其他方法请参见 “Simple Good-Turing”。

4.3 组合估计平滑

不管是拉普拉斯平滑，还是古德图灵平滑技术，对于未出现的n元组都一视同仁，而这难免存在不合理。 因为哪怕是未发生的事件，相互之间真实的概率也会存在差别。

另一方面，一个n元组可能未出现，但是其(n-1)元组或者(n-2)元组是出现过的，这些信息如果不利用就直接浪费掉了。在没有足够的数据对高元n-gram模型进行概率估计时，低元n-gram模型通常可以提供有用的信息。 因此可以利用利用低元n-gram模型的信息对高元n-gram模型进行估计：

如果低元n-gram模型的概率本来就很低，那么就给高元n-gram模型一个较低的估计值；
如果低元n-gram模型有一个中等的概率，那么就给高元n-gram模型一个较高的估计值。

常用的组合估计算法有线性差值法和Katz回退法。具体公式比较复杂，这里就不列了。感兴趣的同学可参考 Christopher D. Manning 的《统计自然语言处理基础》

5. 从N-gram谈回贝叶斯方法

聊了这么多N-gram语言模型，我们再回到贝叶斯方法，从实际应用中看看他们的关联。
最原始的用贝叶斯方法进行分类的公式其实非常简单：