NTU-Coursera机器学习:Types of Learning
本节(各种类型的机器学习分类)总体思路:按照输出空间类型分Y,数据标记类型分yn,不同目标函数类型分f和不同的输入空间类型分X .其中按照输出空间类型Y,可以分为二元分类,多元分类,回归分析以及结构化学习等.
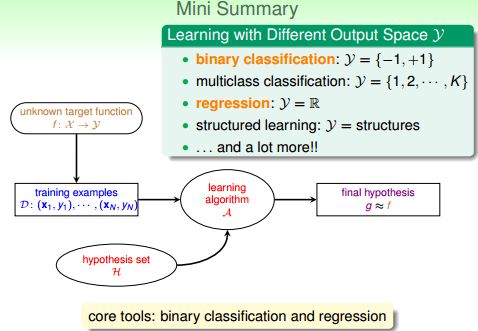
Learning with Different Output Space Y
分类(classification)
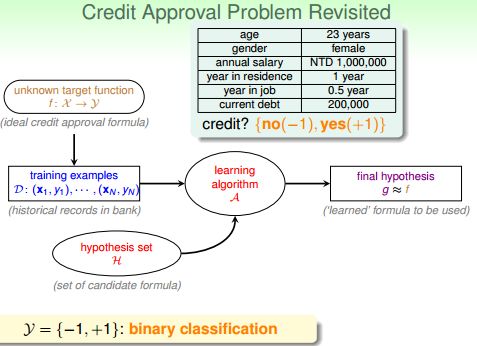
1. 二值分类 (binary classification):输出为 {+1, -1}
那个银行发信用卡的案例中,对于任意用户,输出只可能有两个结果{η}={+1,-1},+1就发卡,-1就不发。这是一个简单的二值分类问题。同样的问题有很多,例如贷款(贷还是不贷)、签证(签还是不签)、答案(对还是不对)、邮件(是不是垃圾邮件)等。
2. 多值分类 (multiclass classification)
而相对二元分类,当然有多元分类问题。例如,美分硬币共有四种(1、5、10、25美分),输入数据为(尺寸,重量),输出集合{η}={1美分,5美分,10美分,25美分}。这是一个4分类问题。
一般的讲,多元分类问题的输出可表示为: {η}={ 1, 2,···,K } (K≥2)
认知行为基本上都是分类问题,比如:
识别数字字符,输出为{η}={1,2,3,4,5,6,7,8,9,0};
通过图像识别水果,输出为{η}={苹果,橘子,香蕉 ··· };
识别垃圾邮件,输出为{η}={垃圾邮件,广告邮件,社交邮件 ··· }。
回归(regression)
regression 中输出空间:实数集 R , 或 区间 [lower, upper]. 想象一下用不同的机器学习方法诊断病人。
- 二分类:病人数据 => { 你有病,你挺好的 };
- 多分类:病人数据 => { 肺炎,感染,禽流感 ··· };
病人数据 => 放心,你有99%的概率在N天后康复........
是不是第三个场景更诱人(Geeky)?这不就是大数据资料挖掘么,当一个机器了解了很多病人的特征、症状和康复数据后,将这些参数作为随机变量,机器能针对特定病人,用统计方法构建这些随机变量的概率密度函数。对于每一个病人,它们的康复就是可预测的了。
类似的问题还有,通过公司数据预测股票价格,通过气象数据预测降水概率等。
====PS:局部加权与线性回归分析python代码====
from numpy import *
def reression(testPoint,trainSet,targetSet):
xMat = mat(trainSet);yMat = mat(targetSet).T;
weight = lineRegression(xMat,yMat);
yHat = xMat*weight;
corrMat = corrcoef(yHat.T,yMat);
'''
|correlationCoefficient| > 0.8时称为高度相关,
当0.5< |correlationCoefficient|<0.8时称为显著相关,
当 0.3<|correlationCoefficient|<0.5时,成为低度相关,
当 |correlationCoefficient| < 0.3时,称为无相关
'''
if corrMat[0,1] < 0.5:
return LWLRegresssion(testPoint,xMat,yMat);
else:
return testPoint*weight;
def lineRegression(xMat,yMat):
'''note:
weight = (X.T*X).I*(X.T*y)
mat.I: 求矩阵的逆
mat.T: 求矩阵的转置
'''
xTx = xMat.T * xMat;
if 0.0 == linalg.det(xTx):
return ridgeRegression(xMat,yMat);
else:
return xTx.I * (xMat.T * yMat);
def LWLRegresssion (testPoint,xMat,yMat,k=1.0):
'''
k: 带宽
weight = (X.T*W*X).I *X.T*W*y
shape(mat): 返回矩阵的行与列,是一个元组结构
eye(m,m) or eye ((m)): 产生m个不同的m维单位向量
'''
r = shape(xMat)[0];
weight = mat(eye((r)));
for j in range(r):
diffMat = testPoint - xMat[j:,];
weight[j,j] = exp(diffMat.T*diffMat/(-2.0*k**2));
xTx = xMat.T*(weight*xMat);
if 0.0 == linalg.det(xTx):
return ridgeRegression(xMat,yMat,True);
else:
return testPoint*(xTx.I*(xMat*(weight*yMat)));
def ridgeRegression(xMat,yMat,q = False,lam=0.2):
xTx = xMat.T;
if q:
w = mat(mat(eye((shape(xMat)[0]))))
xTx *= w*xMat;
else:
xTx *= xMat;
denom = xTx + lam*eye(shape(xMat)[1]);
if 0.0 == linalg.det (demon):
print("matrix is singular, cannot do inverse")
return;
else:
return demon.I*(xMat.T*yMat)
return ===========
结构学习(structured learning)
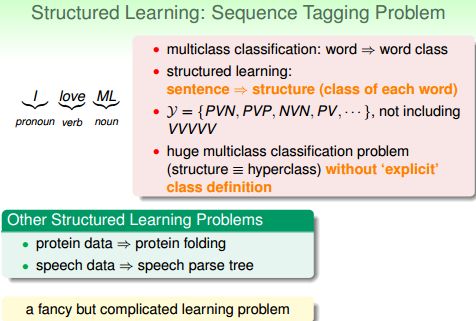
结构学习(structured learning):典型的有序列化标注问题.
这个就高大上了,自然语言处理(NLP)就属于此类问题。比如:这句话中“I”是代词(Pronoun),“Love”是动词(Verb),“ML”是名词(Noun)。它与“PVN”结构匹配。同理,还可以存在“PVP”,"NVN"等很多组合,但一定不包括“VVV”这种不合乎语法的组合。此时,输出集{η}的内容不是显性确定的,而是由一套规则(这里是语法)隐性决定的。所以学习难度增加了。
输出是一个结构(如句子中每个单词的词性), 可以成为 hyperclass, 通常难以显示地定义该类。需要重点研究的是二值分类和回归。
总结
这节主要是讲最基础的算法是二元分类和回归分析,以它们为基础可以构建出更复杂高级的学习算法
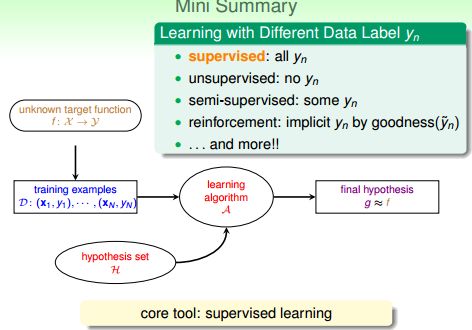
Learning with Different Data Label yn
最常见的对“从例子中学习”的方法的分类是监督学习、非监督学习和强化学习,这是从训练样本的歧义性(ambiguity)来进行分类的。
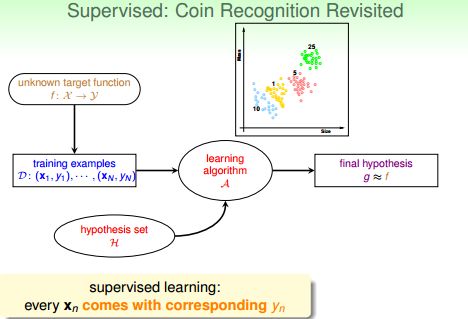
有监督学习(supervised learning)
有监督学习(supervised learning):训练数据中每个xi 对应一个标签yi。它通过对具有概念标记(concept label)的训练例进行学习,以尽可能正确地对训练集之外的示例的概念标记进行预测。这里所有训练例的概念标记都是已知的,因此训练样本的歧义性最低。应用:分类
即每一个有效的输入,都对应一个输出(x(i) -> y(i))。在硬币识别问题中,训练数据集D就是一堆美分硬币的重量与尺寸以及对应的面值。在寻找近似目标函数g的过程中,机器知道在哪些数据上有错误,并能正对错误不断迭代,最终找到犯错最少或不犯错的g函数。
无监督学习(unsupervised learning)
无监督学习(unsupervised learning):没有指明每个xi 对应的是什么,即对x没有label。
即每一个有效的输入都没有对应的输出(没有y(i))。我只给你一堆硬币的重量和尺寸,但我不告诉你对应的面值。所以你能做的只是把它们分成几类,但你并不知道每种类别的意义。
应用:所以无监督学习很适合分群问题,密度估算(density estimation),异常探测等。
分群问题:{x(n)} -> cluster(x)。例如输入文章内容划分文章主题。
密度估算:{x(n)} -> density(x)。例如输入交通数据,确定事故高发区。
异常探测:{x(n)} -> unusual(x)。例如输入网络日志,找到系统异常。
半监督学习(semi-supervised learning)
半监督学习(semi-supervised learning):只有少量标注数据,利用未标注数据。即在训练数据集D中,有一部分x(i)被标注了y(i)。
从训练样本歧义性角度进行的分类体系,在近几年可望有一些扩展,例如多示例学习(multi-instance learning)等从训练样本歧义性方面来看很特殊的新的学习框架有可能会进入该体系。但到目前为止,没有任何新的框架得到了公认的地位。另外,半监督学习(semi-supervised learning)也有一定希望,它的障碍是半监督学习中的歧义性并不是与生俱来的,而是人为的,即用户期望用未标记的样本来辅助对已标记样本的学习。这与监督学习、非监督学习、强化学习等天生的歧义性完全不同。半监督学习中人为的歧义性在解决工程问题上是需要的、有用的(对大量样本进行标记的代价可能是极为昂贵的),但可能不太会导致方法学或对学习问题视点的大的改变。
应用:人脸识别;医药效果检测。
增强学习(reinforcement learning)
增强学习(reinforcement learning):通过隐含信息学习,通常无法直接表示什么是正确的,但是可以通过”惩罚“不好的结果,”奖励“好的结果来优化学习效果。
增强学习的特点是通过与环境的试探性(trial and error)交互来确定和优化动作的选择,以实现所谓的序列决策任务。在这种任务中,学习机制通过选择并执行动作,导致系统状态的变化,并有可能得到某种强化信号(立即回报),从而实现与环境的交互。强化信号就是对系统行为的一种标量化的奖惩。系统学习的目标是寻找一个合适的动作选择策略,即在任一给定的状态下选择哪种动作的方法,使产生的动作序列可获得某种最优的结果(如累计立即回报最大)。在综合分类中,经验归纳学习、遗传算法、联接学习和加强学习均属于归纳学习,其中经验归纳学习采用符号表示方式,而遗传算法、联接学习和加强学习则采用亚符号表示方式;分析学习属于演绎学习。
增强学习学习通常都是顺序进行的。比如用户对垃圾邮件的标注都是一封一封的。实际上,类比策略可看成是归纳和演绎策略的综合。因而最基本的学习策略只有归纳和演绎。应用:广告系统,扑克、棋类游戏。
总结
有监督学习有所有的yi;无监督学习没有yi;半监督学习有少量的yi;增强学习有隐式的yi。
监督和非监督很好理解,半监督和增强其实应用更加普遍,数据的标记大部分时候是需要人来做的,这个条件有时候很难满足(如:经费不足),那么半监督就有比较好的应用了。用人的学习过程来理解,人按照课本去学习,是监督,如果没有课本,按照自己发现的规律去解决问题,则是非监督,因为此,非监督学习的应用相对有限。有时候学习的事物特征到标记结果不是很好描述,例如搜索引擎的广告系统,针对不同用户信息以及query放什么广告,放在什么位置,这需要增强学习去不断的强化,让用户通过点击率反馈机器学习系统使得其不断优化,因为我们自己定义数据标记是很困难的,又例如机器学习开车。因此增强学习的关键在于反馈的存在。
Learning with Different Protocol f (xn, yn)
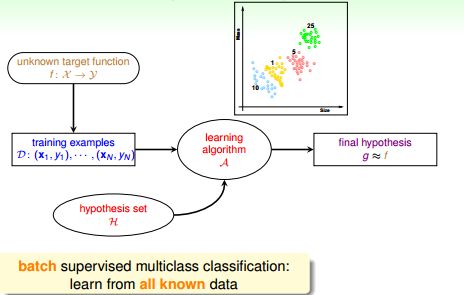
批量学习(Batch learning)
批量学习(Batch learning)利用所有已知训练数据来学习。在线学习 online learning
在线学习online learning通过序列化地接收数据来学习,逐渐提高性能。应用:垃圾邮件, 增强学习。
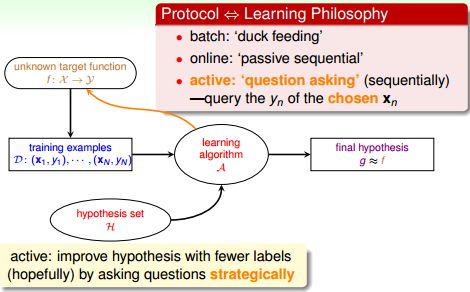
主动学习active learning
通过策略性的提问来改善函数g。例如选择一个x(i),然后问监督者对应的y(i)是什么。
总结
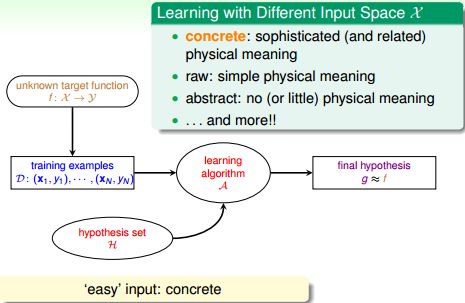
Learning with Different Input Space X
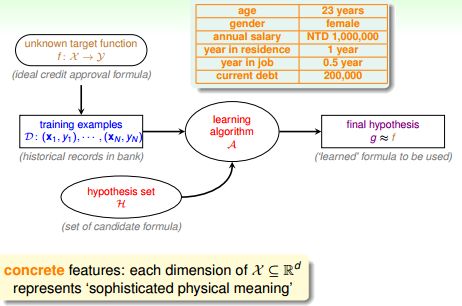
离散特征concrete features
特征中通常包含了人类的智慧。例如对硬币分类需要的特征是(大小,重量);
例如银行客户的数据:年龄、性别、年收入等都是具有社会意义、人类能够识别的数据。对信用分级需要的特征是客户的基本信息。这些特征中已经蕴含了人的思考。
原始特征raw features
以数字识别为例,输入数据是16 x 16像素的黑白数字图片,输出是识别图片中数字的值。对于机器,它只知道像素矩阵中每个像素点的灰度值,这是图像所包含的的最原始的信息。此时,通常需要机器或人类将其转化为具有实质意义的信息。
raw features这些特征对于学习算法来说更加困难,通常需要人或机器(深度学习,deep learning)将这些特征转化为离散(concrete)特征。例如,数字识别中,原始特征是图片的像素矩阵;声音识别中的声波信号;机器翻译中的每个单词。
抽象特征abstract features
抽象特征通常没有任何真实意义,更需要认为地进行特征转化、抽取和再组织。========
PS:
打个比方,我喊一声你好朋友的名字,你在脑海里立刻就能想起他的样子、爱穿什么衣服、爱吃什么菜等信息,就是说输入了一个抽象的名字”李二小“,输出却是关于”李二小“的大量信息。实现的前提是你的数据库里(大脑)已经存储了关于”李二小“的足够数据。
========
例如,预测某用户对电影的评分,原始数据是(userid, itemid, rating), rating 是训练数据的标签,相当于y。这里的(userid, itemid)本身对学习任务是没有任何帮助的,我们必须对数据所进一步处理、提炼、再组织。
总结
离散特征具有丰富的自然含义;原始特征有简单的自然含义;抽象特征没有自然含义。原始特征、抽象特征都需要再处理,此过程成为特征工程(feature engineering),是机器学习、数据挖掘中及其重要的一步。离散特征一般只需要简单选取就够了。
关于Machine Learning更多讨论与交流,敬请关注本博客和新浪微博songzi_tea.