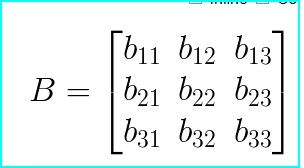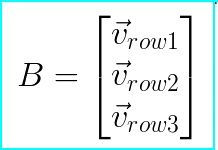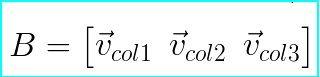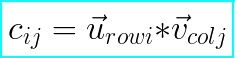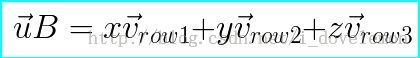DirectX 9.0 (2) 矩阵
引言
在3D图形学中,我们无时无刻不再和矩阵打交道,诸如平移,缩放,旋转等几何变换使用矩阵来进行将会大大的提供效率。所以,有必要对矩阵的相关知识做基本的了解。
矩阵定义
一个m*n的矩阵表示的就是一个拥有m行,n列的矩形数组。在数组中的数,我们称之为元素。对元素进行描述时,我们使用它在这个矩阵中的行数和列数作为它的下标来表示,下图就是一个矩阵:
矩阵可以看做是一些向量的集合。我们既可以把矩阵中的一行做为一个向量,也可以将一列做为一个向量,如下所示:
其中Vrow1 = {b11, b12, b13}, Vrow2 = {b21, b22, b23}, Vrow3 = {b31, b32, b33}
又如下图中的列向量表示法:
其中Vcol1 = {b11, b21, b31}, Vcol2 = {b12, b22, b32}, Vcol3 = {b13, b23, b33}
在DirectX中大部分时候都是采用行向量的表示方法,而在OpenGL中一般采用列向量的表示方法,所以如果您看过不同的书籍,会看到上面介绍的关于旋转,缩放,平移等矩阵有一点点不同,他们可能相互为倒置关系(倒置关系将在下面介绍),这就是因为有的书在讲述的时候使用的是行向量,比如龙书,有的书讲述的时候使用的是列向量,比如Real-time rendering。希望读者仔细区分,我在下面将会一直使用行向量的表示方法来描述问题。
矩阵操作
- 两个矩阵相等,只要他们相对应的元素一一相等就可以。这也就是说两个矩阵相等,他们的列数和行数一定也互相相等,否则没有办法比较。
- 两个矩阵相加,只要将对应的元素一一相加即可。同样的,这两个矩阵的行数和列数也一定要相同
- 一个标量乘以一个矩阵,只要将这个标量乘以矩阵中每一个元素即可
矩阵乘法
矩阵乘法,是矩阵很重要的一个运算,也是矩阵体现高效率的原因所在。两个矩阵要能够进行矩阵乘法,他们需要满足一些条件。
如果A是一个m*n矩阵,B是一个n*p矩阵,那么A*B的结果就是一个m*p矩阵。
从这个例子,我们大概能够猜测到矩阵可以进行乘法的条件就是A的列数一定要等于B的行数,只有这样才能够进行矩阵乘法,乘法的结果是以A的行数和B的列数为行数和列数的矩阵。
进行乘法运算是是使用如下的公式进行:
也就是说C矩阵为A矩阵和B矩阵相乘之后的结果,C矩阵中的第Cij个元素为A矩阵中的i行向量与B矩阵中的j列向量点积之后的结果。
我们需要注意由于矩阵的特殊性,一般情况下,它并不满足乘法交换律,也就是说A* B 不等于B*A。从上面的例子我们就可以看出,B* A要是能够相乘的话,B的列数一定要等于A的行数才可以,但是他们可能并不相等,所以并不满足交换律。
向量-矩阵乘法
学习矩阵的主要目的,就是对向量进行运算。我们知道,在3D模型中,都是使用三角形来表示的,而三角形又是使用3个顶点来表示的,顶点又是使用3D向量来表示的,所以对顶点进行变换,就能够达到对三角形,多边形,乃至整个物体进行变换了。
我们来考虑如下的向量-矩阵乘法:
我们可以将向量u看成是一个1*3的矩阵,这样uB的结果也就是一个1*3的矩阵了。
通过将结果进行推导我们可以得到如下的公式:
读者可能看到上面的公式有点熟悉,是的,这和我们在前一节中讲述向量的坐标变换的公式一样,只要我们将这里的Vrow1,Vrow2,Vrow3变成相对于某个坐标系的本坐标系基坐标的表示,我们就可以得出变换后的结果了。
也就是说,我们可以是用向量-矩阵的方法来对一个向量进行坐标变换,只要我们知道A坐标系中的基坐标(x轴,y轴,z轴)在B坐标系下的表示Vrow1,Vrow2,Vrow3,我们就可以使用矩阵计算出变换后的结果了。很方便是吧。
读者可能会问,你这个是对向量的坐标变换使用矩阵的方法,那么对于点向量又是怎么样了???
正如您想的那样,他们之间很不同,而且大大的不同,需要重新领入一个新的概念,所以将留在下一篇中专门讨论这个问题。
矩阵倒置(Transpose)
矩阵倒置,指的是将矩阵中原来的行向量,和列向量互换,如下图所示:
其中AT就是对矩阵倒置的操作符
矩阵求逆
矩阵求逆的运算比较复杂,但是不难理解,任何一本线性代数的书上都会有这样的运算解释,所以这里就不再赘述。但是需要明白的一点是,矩阵上面没有定义除法运算,所以才定义了一个矩阵求逆的运算。也就是说,通过逆运算,可以将原本变换后的物体,在将相同的矩阵进行求逆之后,在变换,就可以变换会原来的样子。
总结
好了,暂时就讲到这里了!!!欢迎大家指出错误!!!