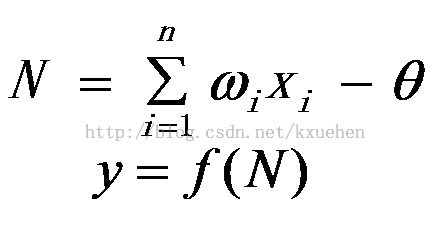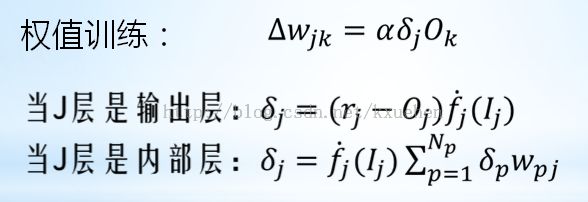神经网络编程及其训练
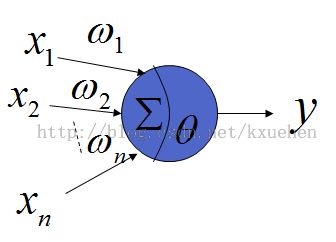
1.神经元结构
每个神经元包含权值、输入值、激活元素,误差项,阀值组成。在这里用一个结构体Nerver来表示,其中Weights_Temp[20],这个数组在批处理训练的时候会用来,保存个样本训练后权值的改变量。
typedef struct
{
float Weights[20]; //权值
float Weights_Temp[20]; //批处理时临时权值
float Activating_Element; //激活元素Iq
float OutPut; //神经元输出
float Error; //误差项
float Threshold; //阀值
}Nerver; //神经元结构体
神经元输出与前一层的输入,本层的权值,阀值之间的关系为:
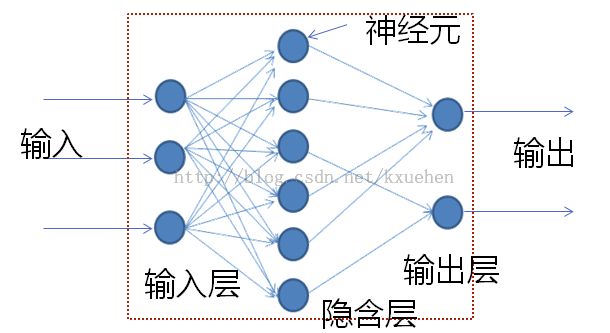
2. 3层的神经网络
for (i=1;i<=Lay_Number;i++) //Lay_Number 是神经网络的层数,本例中取4层
{
for (j=0;j<Lay_Arrangement[i];j++)//Lay_Arrangement是每层中节点个数
{
for (k=0;k<Lay_Arrangement[i-1];k++)
{
Sum+=NetWeb[i-1][k].OutPut*NetWeb[i][j].Weights[k];//NetWeb是Nerver结构体的一个对象
}
NetWeb[i][j].Activating_Element=Sum+NetWeb[i][j].Threshold;
Sum=0;
NetWeb[i][j].OutPut=(a/(1+exp(-NetWeb[i][j].Activating_Element/thta)));//第i层第j个神经元的输出值y
}
} //计算每个神经元的值
在这里神经网络的正向计算已经完成,其中权值、阀值,训练样本的初始化这些工作在后面的完整代码中给出。
3. 权值的训练过程
反向传播模型采用德尔塔原则:
均方误差:
权值训练,相邻两层间误差项的递推关系:
每层每个节点误差项的计算如下:
for(Cal=0;Cal<1;Cal++)
{
NetWeb[Lay_Number][Cal].Error=(Optimal_Value[m]-NetWeb[Lay_Number][Cal].OutPut)*a/thta*NetWeb[Lay_Number][Cal].OutPut*(1-NetWeb[Lay_Number][Cal].OutPut);//输出层误差项的计算
Sum_Error+=abs(Optimal_Value[m]-NetWeb[Lay_Number][Cal].OutPut); //累计误差
} //输出层的各节点误差项
for (i=Lay_Number-1;i>0;i--)
{
for (j=0;j<Lay_Arrangement[i];j++)
{
for (k=0;k<Lay_Arrangement[i+1];k++)
{
Sum+=NetWeb[i+1][k].Error*NetWeb[i+1][k].Weights[j];
}
NetWeb[i][j].Error=Sum*a/thta*NetWeb[i][j].OutPut*(1-NetWeb[i][j].OutPut);
Sum=0;
}
} //利用递推关系计算每层每节点误差项
对一个样本训练后利用每个节点的误差项,得到每层每节点的权值变化量,由于程序中使用批处理的方式,也就是当所有样本全部训练完一次后在改变网络中的权值,所以每个样本训练后,得到的权值改变量会累加到相应的数组NetWeb[i][j].Weights_Temp[k]中:
for (i=1;i<=Lay_Number;i++)
{
for (j=0;j<Lay_Arrangement[i];j++)
{
for (k=0;k<Lay_Arrangement[i-1];k++)
{
NetWeb[i][j].Weights_Temp[k]+=Learn_Coefficient*NetWeb[i][j].Error*NetWeb[i-1][k].OutPut;
}
}
} //计算训练一个样本后得权值改变累计
所用样本都训练完一次后,对网络权值进行更新:
for (i=1;i<=Lay_Number;i++)
{
for (j=0;j<Lay_Arrangement[i];j++)
{
for (k=0;k<Lay_Arrangement[i-1];k++)
{
NetWeb[i][j].Weights[k]+=NetWeb[i][j].Weights_Temp[k];
}
}
} //一个训练批次后,更新权值
4.训练结果
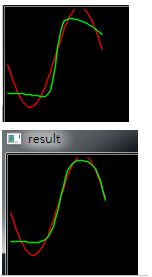
程序中采用了一个输入层,两个隐层和一个输入层的结构。每次训练结果会有所差异。误差总会存在,还存在许多改进的地方,不过作为一个理解神经网络基本运作原理来说已经够了。
目标函数选择 (sin(2*3.1415926*x)+1)/2。训练范围为(0,1)。
对于样本的选取,最好将输入与输出规范化到(0,1)中这样训练效果会比较好。程序中S函数参数选取为a=1.716,thta=1。a的值要比目标函数的最大值要大,这样训练才能成功。
5.源代码
该源代码使用了opencv显示图像,需要包含opencv库,可能由于各个电脑程序库不同,并不一定可以直接运行。但各个功能部分是可以使用的,本程序可以实现任意层数与节点的神经网络。
#include <stdio.h>
#include <tchar.h>
#include "function.h"
#include <math.h>
#include "opencv2/opencv.hpp"
#include <ctime>
#include <cstdlib>
using namespace cv;#define NUM 40
double random(double,double);typedef struct
{
float Weights[20]; //权值
float Weights_Temp[20]; //批处理时临时权值
float Activating_Element; //激活元素Iq
float OutPut; //神经元输出
float Error; //误差项
float Threshold; //阀值
}Nerver; //神经元结构体
int _tmain(int argc, _TCHAR* argv[])
{
unsigned int Lay_Arrangement[10],i,j,k,m,Lay_Number=3,Learn_Num=0,Sample_Num=NUM,Cal=0;
float Sum=0,Optimal_Value[NUM+1],Learn_Coefficient=0.01,x,Sum_Error=100000,a=1.716,thta=1;
Lay_Arrangement[0]=1;
Lay_Arrangement[1]=3;
Lay_Arrangement[2]=2;
Lay_Arrangement[3]=1;
Nerver NetWeb[10][NUM];
srand(unsigned(time(0)));
IplImage *im;
CvPoint PrePoint,Point;
CvScalar m_RGB;
for (i=1;i<=Lay_Number;i++) //i层
{
for (j=0;j<Lay_Arrangement[i];j++) //第j个节点
{
NetWeb[i][j].Threshold=0; //初始化神经元阀值
}
}
for (i=1;i<=Lay_Number;i++) //i层
{
for (j=0;j<Lay_Arrangement[i];j++) //第j个节点
{
for (k=0;k<Lay_Arrangement[i-1];k++) // 第i层第j个节点与前一层第k个节点之间的权值初始值
{
NetWeb[i][j].Weights[k]=random(-0.5,0.5);
//NetWeb[i][j].Weights[k]=0.1;
NetWeb[i][j].Weights_Temp[k]=0;
}
}
}
for(x=0.0;x<PI;x+=PI/Sample_Num)
{
NetWeb[0][Cal].OutPut=x; //神经元输入值
Optimal_Value[Cal]=(sin(2*3.1415926*x)+1)/2; //神经元理想输出值
//Optimal_Value[Cal]=sin(x);
Cal++;
} //初始化神经网络输入层
while ((Sum_Error>0.0001)&&(Learn_Num<40000))
{
Sum_Error=0;
Learn_Num++;
for (i=1;i<=Lay_Number;i++) //i层
{
for (j=0;j<Lay_Arrangement[i];j++) //第j个节点
{
for (k=0;k<Lay_Arrangement[i-1];k++) // 第i层第j个节点与前一层第k个节点之间的权值初始值
{
NetWeb[i][j].Weights_Temp[k]=0;
}
}
}
for(m=0;m<Sample_Num;m++)
{
NetWeb[0][0].OutPut=NetWeb[0][m].OutPut;
for (i=1;i<=Lay_Number;i++)
{
for (j=0;j<Lay_Arrangement[i];j++)
{
for (k=0;k<Lay_Arrangement[i-1];k++)
{
Sum+=NetWeb[i-1][k].OutPut*NetWeb[i][j].Weights[k];
}
NetWeb[i][j].Activating_Element=Sum+NetWeb[i][j].Threshold;
Sum=0;
NetWeb[i][j].OutPut=(a/(1+exp(-NetWeb[i][j].Activating_Element/thta)));
}
} //计算每个神经元的值
for(Cal=0;Cal<1;Cal++)
{
NetWeb[Lay_Number][Cal].Error=(Optimal_Value[m]-NetWeb[Lay_Number][Cal].OutPut)*a/thta*NetWeb[Lay_Number][Cal].OutPut*(1-NetWeb[Lay_Number][Cal].OutPut);
Sum_Error+=abs(Optimal_Value[m]-NetWeb[Lay_Number][Cal].OutPut); //累计误差
} //输出层的各节点误差项
for (i=Lay_Number-1;i>0;i--)
{
for (j=0;j<Lay_Arrangement[i];j++)
{
for (k=0;k<Lay_Arrangement[i+1];k++)
{
Sum+=NetWeb[i+1][k].Error*NetWeb[i+1][k].Weights[j];
}
NetWeb[i][j].Error=Sum*a/thta*NetWeb[i][j].OutPut*(1-NetWeb[i][j].OutPut);
Sum=0;
}
} //计算每层每节点误差项
for (i=1;i<=Lay_Number;i++)
{
for (j=0;j<Lay_Arrangement[i];j++)
{
for (k=0;k<Lay_Arrangement[i-1];k++)
{
NetWeb[i][j].Weights_Temp[k]+=Learn_Coefficient*NetWeb[i][j].Error*NetWeb[i-1][k].OutPut;
}
}
} //计算训练一个样本后得权值改变累计
}
for (i=1;i<=Lay_Number;i++)
{
for (j=0;j<Lay_Arrangement[i];j++)
{
for (k=0;k<Lay_Arrangement[i-1];k++)
{
NetWeb[i][j].Weights[k]+=NetWeb[i][j].Weights_Temp[k];
}
}
} //一个训练批次后,更新权值
}
im=cvCreateImage(cvSize(1400,400),IPL_DEPTH_8U,3);
Mat im_Mat(im);
cvZero(im);
PrePoint=cvPoint(0,100);
m_RGB=CV_RGB(255,0,0);
x=0;
for(Cal=0.0;Cal<Sample_Num;Cal++)
{
Point=cvPoint(int(100*x),int(100*Optimal_Value[Cal]));
cvLine(im, PrePoint, Point,m_RGB,1,CV_AA,0);
PrePoint=Point;
x+=PI/Sample_Num;
}
m_RGB=CV_RGB(0,255,0);
PrePoint=cvPoint(0,int((NetWeb[Lay_Number][Cal].OutPut)*100));
x=0;
for (i=1;i<=Lay_Number;i++)
{
for (j=0;j<Lay_Arrangement[i];j++)
{
for (k=0;k<Lay_Arrangement[i-1];k++)
{
printf("%f1.4 ",NetWeb[i][j].Weights[k]);
}
}
printf("\n");
} //一个训练批次后,更新权值
for(Cal=0.0;Cal<Sample_Num;Cal++)
{
NetWeb[0][0].OutPut=x;
for (i=1;i<=Lay_Number;i++)
{
for (j=0;j<Lay_Arrangement[i];j++)
{
for (k=0;k<Lay_Arrangement[i-1];k++)
{
Sum+=NetWeb[i-1][k].OutPut*NetWeb[i][j].Weights[k];
}
NetWeb[i][j].Activating_Element=Sum+NetWeb[i][j].Threshold;
Sum=0;
NetWeb[i][j].OutPut=(a/(1+exp(-NetWeb[i][j].Activating_Element/thta)));//利用训练后网络实现对目标函数的拟合
}
}
Point=cvPoint(int(100*x),int(100*(NetWeb[Lay_Number][0].OutPut)));
cvLine(im, PrePoint, Point,m_RGB,1,CV_AA,0);
PrePoint=Point;
x+=PI/Sample_Num;
}
imshow("result",im_Mat);
waitKey(0);
return 0;
}
double random(double start, double end)
{
return start+(end-start)*rand()/(RAND_MAX + 1.0);
}