LeetCode 37 Sudoku Solver(求解数独)(*)
翻译
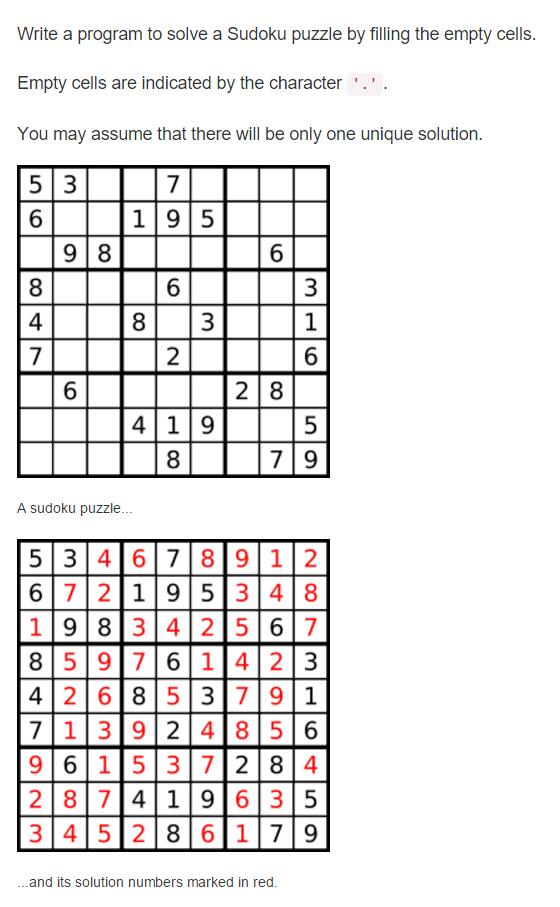
写一个程序来通过填充空格求解数独。
空格用'.'表示。
你可以假定这里只有唯一解。
(示例图片看下文)原文
代码
这道题我没写……不过为了博客的连续性,先凑一篇占个位置,以后再修改。
class Solution {
public:
bool col[10][10],row[10][10],f[10][10];
bool flag = false;
void solveSudoku(vector<vector<char>>& board) {
memset(col,false,sizeof(col));
memset(row,false,sizeof(row));
memset(f,false,sizeof(f));
for(int i = 0; i < 9;i++){
for(int j = 0; j < 9;j++){
if(board[i][j] == '.') continue;
int temp = 3*(i/3)+j/3;
int num = board[i][j]-'0';
col[j][num] = row[i][num] = f[temp][num] = true;
}
}
dfs(board,0,0);
}
void dfs(vector<vector<char>>& board,int i,int j){
if(flag == true) return ;
if(i >= 9){
flag = true;
return ;
}
if(board[i][j] != '.'){
if(j < 8) dfs(board,i,j+1);
else dfs(board,i+1,0);
if(flag) return;
}
else{
int temp = 3*(i/3)+j/3;
for(int n = 1; n <= 9; n++){
if(!col[j][n] && !row[i][n] && !f[temp][n]){
board[i][j] = n + '0';
col[j][n] = row[i][n] = f[temp][n] = true;
if(j < 8) dfs(board,i,j+1);
else dfs(board,i+1,0);
col[j][n] = row[i][n] = f[temp][n] = false;
if(flag) return;
}
}
board[i][j] = '.';
}
}
};class Solution {
// Table which allows compute the value of the cell
// from the unambiguous bit mask as maskToValue[(mask%11)-1]
// uses the fact that (1<<i)%11 is unique for i = [0..8] and never produces 0
const char maskToValue[10] = {'1','2','9','3','5','6','8','4','7','6'};
struct SudokuSolver {
// Using mask for each cell which constraints values which can be in the cell
// Yeap, it is more storage, comparing to rows/cols/sqrs approach
// but it allows to do super-fast reactive constraint propagation
array<array<uint16_t,9>,9> board;
SudokuSolver()
{
// Initializing the board with mask, which permits all numbers
for (int i=0; i<9; i++)
for (int j=0; j<9; j++)
board[i][j] = 0x1ff;
}
// adds value v [1..9] to the board, return false if it violates constraints
bool add(int i, int j, int v)
{
return set(i, j, 1<<(v-1));
}
// set a value mask to the cell (i,j) and reactively updates constraints
bool set(int i, int j, uint16_t mask)
{
int16_t prev = board[i][j];
if (prev == mask) return true;
if (!(prev&mask)) return false;
board[i][j] = mask;
return propagate(i,j,mask);
}
// propagates constraints as a result of setting i,j to mask
bool propagate(int i, int j, uint16_t mask)
{
for (int k=0; k<9; k++) {
if (k!=j && !addConstraint(i, k, mask)) return false;
if (k!=i && !addConstraint(k, j, mask)) return false;
int ii = (i/3)*3 + (k/3);
int jj = (j/3)*3 + (k%3);
if ((i != ii || j != jj) && !addConstraint(ii, jj, mask)) return false;
}
return true;
}
// prohibits putting value in mask to the cell (i,j)
bool addConstraint(int i, int j, uint16_t mask)
{
int16_t newMask = board[i][j] &~ mask;
if (newMask != board[i][j]) {
if (newMask == 0) return false;
board[i][j] = newMask;
if (((newMask-1)&newMask)==0) {
// good news - we have only one possibility for the cell (i,j)
return propagate(i, j, newMask);
}
}
return true;
}
// list of cell coordinates with >1 possibilities for values
vector<pair<int,int>> v;
void solve()
{
// finding all ambiguous cells
for (int i=0; i<9; i++) {
for (int j=0; j<9; j++) {
uint16_t mask = board[i][j];
if (mask&(mask-1)) v.push_back(make_pair(i,j));
}
}
// note: it is also a good idea to sort v by the hamming weight, but
// without sorting it is still super-fast
// running backtracking as is
backtrack(0);
}
// backtracking
bool backtrack(int k) {
if (k == v.size()) return true;
int i = v[k].first;
int j = v[k].second;
uint16_t mask = board[i][j];
if (mask&(mask-1)) {
// the board state is so compact and backtracking depth is so shallow, so
// it is cheaper to make a snapshot of the state vs. doing classical
// undo at each move
auto snapshot = board;
for (uint16_t cand = 1; cand<=0x1ff; cand = cand <<1) {
if (set(i, j, cand) && backtrack(k+1)) return true;
board = snapshot;
}
return false;
}
else {
return backtrack(k + 1);
}
}
};
public:
void solveSudoku(vector<vector<char>>& board) {
SudokuSolver solver;
for (int i=0; i<9; i++) {
for (int j=0; j<9; j++) {
char c = board[i][j];
if (c != '.' && !solver.add(i,j,c-'0')) return;
}
}
// At this point 9 of 10 sudokus published in magazines will be solved by constraint propagation
// only 'hard' sudokus will require some (limited) backtracking
solver.solve();
for (int i=0; i<9; i++)
for (int j=0; j<9; j++)
board[i][j] = maskToValue[(solver.board[i][j]%11)-1];
}
};一定要每天坚持呐……