SciPy教程 - sparse module稀疏矩阵

http://blog.csdn.net/pipisorry/article/details/41762945

sparse matrix稀疏矩阵不同的存储形式在sparse模块中对应如下

bsr_matrix(arg1[, shape, dtype,copy, blocksize]) Block Sparse Row matrix

coo_matrix(arg1[, shape, dtype,copy]) A sparse matrix in COOrdinate format.

csc_matrix(arg1[, shape, dtype,copy]) Compressed Sparse Column matrix

csr_matrix(arg1[, shape, dtype,copy]) Compressed Sparse Row matrix

dia_matrix(arg1[, shape, dtype,copy]) Sparse matrix with DIAgonal storage

dok_matrix(arg1[, shape, dtype,copy]) Dictionary Of Keys based sparse matrix.

lil_matrix(arg1[, shape, dtype,copy]) Row-based linked list sparse matrix
不同稀疏矩阵的介绍和优缺点
scipy.sparse库中提供了多种表示稀疏矩阵的格式，每种格式都有不同的用处。 Sparse matrices can be used in arithmetic operations: they support addition, subtraction, multiplication, division,and matrix power.
bsr_matrix(arg1, shape=None, dtype=None, copy=False, blocksize=None)Block Sparse Row matrix
The Block Compressed Row (BSR) format is very similar to the Compressed Sparse Row (CSR) format. BSR is appropriate for sparse matrices with dense sub matrices. Block matrices often arise in vector-valued finite element discretizations. In such cases, BSR is considerably more efficient than CSR and CSC for many sparse arithmetic operations.
csc_matrix(arg1,shape=None, dtype=None, copy=False)压缩的列稀疏矩阵

Advantages of the CSC format
•efficient arithmetic operations CSC + CSC, CSC * CSC, etc.
•efficient column slicing
•fast matrix vector products (CSR, BSR may be faster!)
Disadvantages of the CSC format
•slow row slicing operations (consider CSR)
•changes to the sparsity structure are expensive (consider LIL or DOK)

csr_matrix(arg1, shape=None, dtype=None, copy=False)Compressed Sparse Row matrix

Advantages of the CSR format
•efficient arithmetic operations CSR + CSR, CSR * CSR, etc.
•efficient row slicing
•fast matrix vector products
Disadvantages of the CSR format
•slow column slicing operations (consider CSC)
•changes to the sparsity structure are expensive (consider LIL or DOK)

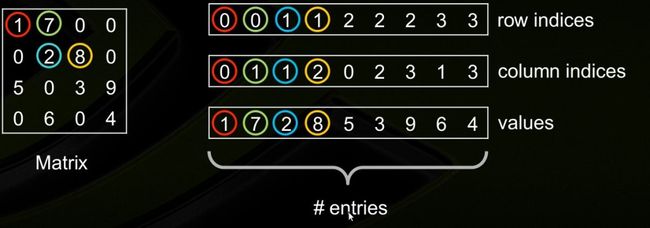
coo_matrix(arg1,shape=None,dtype=None,copy=False):坐标形式的一种稀疏矩阵。采用三个数组row、col和data保存非零元素的信息。这三个数组的长度相同，row保存元素的行，col保存元素的列，data保存元素的值。

coo_matrix不支持元素的存取和增删，一旦创建之后，除了将之转换成其它格式的矩阵，几乎无法对其做任何操作和矩阵运算。

Advantages of the COO format
•facilitates fast conversion among sparse formats
•permits duplicate entries (see example)
•very fast conversion to and from CSR/CSC formats

优点：快速的和CSR/CSC formats转换、允许重复录入. coo_matrix支持重复元素。

Disadvantages of the COO format
•does not directly support:
–arithmetic operations
–slicing

缺点：不能直接进行科学计算和切片操作

最常用的函数：

tocsc()	Return a copy of this matrix in Compressed Sparse Column format
tocsr()	Return a copy of this matrix in Compressed Sparse Row format
todense([order, out])	Return a dense matrix representation of this matrix

ps:许多稀疏矩阵的数据都是采用这种格式保存在文件中的，例如某个CSV文件中可能有这样三列：“用户ID，商品ID，评价值”。采用numpy.loadtxt或pandas.read_csv将数据读入之后，可以通过coo_matrix快速将其转换成稀疏矩阵：矩阵的每行对应一位用户，每列对应一件商品，而元素值为用户对商品的评价。

dia_matrix(arg1, shape=None, dtype=None, copy=False)Sparse matrix with DIAgonal storage

dok_matrix(arg1, shape=None, dtype=None, copy=False)Dictionary Of Keys based sparse matrix.

This is an efficient structure for constructing sparse matrices incrementally.Allows for efficient O(1) access of individual elements. Duplicates are not allowed. Can be efficiently converted to a coo_matrix once constructed.

dok_matrix从dict继承，它采用字典保存矩阵中不为0的元素：字典的键是一个保存元素(行,列)信息的元组，其对应的值为矩阵中位于(行,列)中的元素值。显然字典格式的稀疏矩阵很适合单个元素的添加、删除和存取操作。通常用来逐渐添加非零元素，然后转换成其它支持快速运算的格式。

lil_matrix(arg1, shape=None, dtype=None, copy=False)Row-based linked list sparse matrix
This is an efficient structure for constructing sparse matrices incrementally.

lil_matrix使用两个列表保存非零元素。data保存每行中的非零元素，rows保存非零元素所在的列。这种格式也很适合逐个添加元素，并且能快速获取行相关的数据。

Advantages of the LIL format
•supports flexible slicing
•changes to the matrix sparsity structure are efficient
Disadvantages of the LIL format
•arithmetic operations LIL + LIL are slow (consider CSR or CSC)
•slow column slicing (consider CSC)
•slow matrix vector products (consider CSR or CSC)
Intended Usage
•LIL is a convenient format for constructing sparse matrices
•once a matrix has been constructed, convert to CSR or CSC format for fast arithmetic and matrix vector operations
•consider using the COO format when constructing large matrices

Note:{dok_matrix和lil_matrix适合逐渐添加元素}

[scipy-ref-0.14.0 - Sparse matrices (scipy.sparse)]

[用Python做科学计算-第二版SciPy-数值计算库-稀疏矩阵-sparse]

皮皮blog

Sparse Matrix Storage Formats稀疏矩阵的存储格式

对于很多元素为零的稀疏矩阵，仅存储非零元素可使矩阵操作效率更高。

现有许多种稀疏矩阵的存储方式，但是多数采用相同的基本技术，即存储矩阵所有的非零元素到一个线性数组中，并提供辅助数组来描述原数组中非零元素的位置。

1. Coordinate Format (COO)

这种存储方式的主要优点是灵活、简单。仅存储非零元素以及每个非零元素的坐标。

使用3个数组进行存储：values, rows, andcolumn

values: 实数或复数数据，包括矩阵中的非零元素， 顺序任意。

rows: 数据所处的行。

columns: 数据所处的列.

参数：矩阵中非零元素的数量 nnz，3个数组的长度均为nnz.

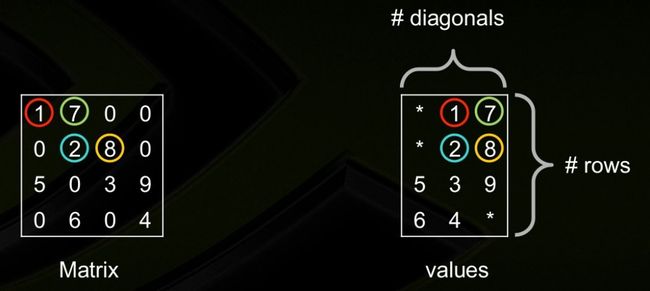
2. Diagonal Storage Format (DIA)

If the sparse matrix has diagonals containing only zero elements, then the diagonal storage format can be used to reduce the amount of information needed to locate the non-zero elements. This storage format is particularly useful in many applications where the matrix arises from a finite element or finite difference discretization.

The Intel MKL diagonal storage format is specified by two arrays:values anddistance, and two parameters:ndiag, which is the number of non-empty diagonals, andlval, which is the declared leading dimension in the calling (sub)programs. 

values

A real or complex two-dimensional array is dimensioned aslval byndiag. Each column of it contains the non-zero elements of certain diagonal ofA. The key point of the storage is that each element invalues retains the row number of the original matrix. To achieve this diagonals in the lower triangular part of the matrix are padded from the top, and those in the upper triangular part are padded from the bottom. Note that the value ofdistance(i) is the number of elements to be padded for diagonali.

distance

An integer array with dimension ndiag. Elementi of the arraydistance is the distance betweeni-diagonal and the main diagonal. The distance is positive if the diagonal is above the main diagonal, and negative if the diagonal is below the main diagonal. The main diagonal has a distance equal to zero.

3. Compressed Sparse Row Format (CSR)

The Intel MKL compressed sparse row (CSR) format is specified by four arrays: thevalues,columns,pointerB, andpointerE. The following table describes the arrays in terms of the values, row, and column positions of the non-zero elements in a sparse matrixA.

values

A real or complex array that contains the non-zero elements ofA. Values of the non-zero elements ofA are mapped into thevalues array using the row-major storage mapping described above.

columns

Element i of the integer array columns is the number of the column inA that contains thei-th value in thevalues array.

pointerB

Element j of this integer array gives the index of the element in thevalues array that is first non-zero element in a rowj ofA. Note that this index is equal topointerB(j) -pointerB(1)+1 .

pointerE

An integer array that contains row indices, such thatpointerE(j)-pointerB(1) is the index of the element in thevalues array that is last non-zero element in a row j of A.

4. Compressed Sparse Column Format (CSC)

The compressed sparse column format (CSC) is similar to the CSR format, but the columns are used instead the rows. In other words, the CSC format is identical to the CSR format for the transposed matrix. The CSR format is specified by four arrays: values, columns, pointerB, and pointerE. The following table describes the arrays in terms of the values, row, and column positions of the non-zero elements in a sparse matrixA.

values

A real or complex array that contains the non-zero elements ofA. Values of the non-zero elements ofA are mapped into thevalues array using the column-major storage mapping.

rows

Element i of the integer array rows is the number of the row inA that contains thei-th value in thevalues array.

pointerB

Element j of this integer array gives the index of the element in thevalues array that is first non-zero element in a columnj ofA. Note that this index is equal topointerB(j) -pointerB(1)+1 .

pointerE

An integer array that contains column indices, such thatpointerE(j)-pointerB(1) is the index of the element in thevalues array that is last non-zero element in a column j ofA.

5. Skyline Storage Format

The skyline storage format is important for the direct sparse solvers, and it is well suited for Cholesky or LU decomposition when no pivoting is required.

The skyline storage format accepted in Intel MKL can store only triangular matrix or triangular part of a matrix. This format is specified by two arrays:values andpointers. The following table describes these arrays:

values

A scalar array. For a lower triangular matrix it contains the set of elements from each row of the matrix starting from the first non-zero element to and including the diagonal element. For an upper triangular matrix it contains the set of elements from each column of the matrix starting with the first non-zero element down to and including the diagonal element. Encountered zero elements are included in the sets.

pointers

An integer array with dimension (m+1), where m is the number of rows for lower triangle (columns for the upper triangle).pointers(i) -pointers(1)+1 gives the index of element invalues that is first non-zero element in row (column)i. The value ofpointers(m+1) is set tonnz+pointers(1), wherennz is the number of elements in the arrayvalues.

6. Block Compressed Sparse Row Format (BSR)

The Intel MKL block compressed sparse row (BSR) format for sparse matrices is specified by four arrays:values,columns,pointerB, andpointerE. The following table describes these arrays.

values

A real array that contains the elements of the non-zero blocks of a sparse matrix. The elements are stored block-by-block in row-major order. A non-zero block is the block that contains at least one non-zero element. All elements of non-zero blocks are stored, even if some of them is equal to zero. Within each non-zero block elements are stored in column-major order in the case of one-based indexing, and in row-major order in the case of the zero-based indexing.

columns

Element i of the integer array columns is the number of the column in the block matrix that contains thei-th non-zero block.

pointerB

Element j of this integer array gives the index of the element in thecolumns array that is first non-zero block in a rowj of the block matrix.

pointerE

Element j of this integer array gives the index of the element in thecolumns array that contains the last non-zero block in a rowj of the block matrix plus 1.

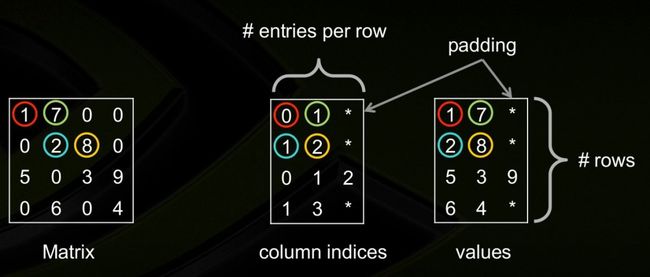
7.  ELLPACK (ELL)

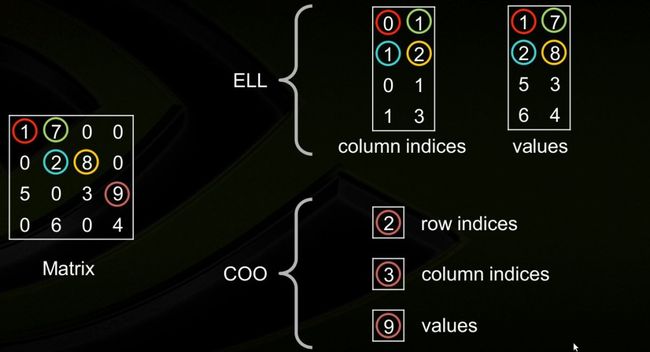
8. Hybrid (HYB)  

由ELL+COO两种格式结合而成。

皮皮blog

选择稀疏矩阵存储格式的一些经验：

1. DIA和ELL格式在进行稀疏矩阵-矢量乘积(sparse matrix-vector products)时效率最高，所以它们是应用迭代法(如共轭梯度法)解稀疏线性系统最快的格式；

2. COO和CSR格式比起DIA和ELL来，更加灵活，易于操作；

3. ELL的优点是快速，而COO优点是灵活，二者结合后的HYB格式是一种不错的稀疏矩阵表示格式；

4. 根据Nathan Bell的工作：

CSR格式在存储稀疏矩阵时非零元素平均使用的字节数(Bytes per Nonzero Entry)最为稳定（float类型约为8.5，double类型约为12.5）

而DIA格式存储数据的非零元素平均使用的字节数与矩阵类型有较大关系，适合于StructuredMesh结构的稀疏矩阵（float类型约为4.05，double类型约为8.10）

对于Unstructured Mesh以及Random Matrix,DIA格式使用的字节数是CSR格式的十几倍；

5. 一些线性代数计算库：COO格式常用于从文件中进行稀疏矩阵的读写，如matrix market即采用COO格式，而CSR格式常用于读入数据后进行稀疏矩阵计算。

[Sparse Matrix Representations & Iterative Solvers, Lesson 1 by Nathan Bell]

[稀疏线性系统 Sparse Linear Systems]

[Intel MKL 库中使用的稀疏矩阵格式]

皮皮blog

sparse matrix稀疏矩阵的相关操作
创建稀疏矩阵
以coo_matrix为例：

1 直接将dense矩阵转换成稀疏矩阵

A =coo_matrix([[1,2],[3,4]])
print(A)
  (0, 0)    1
  (0, 1)    2
  (1, 0)    3
  (1, 1)    4

2 按照相应存储形式的要求构建矩阵：

row  = array([0,0,0,0,1,3,1])
col  = array([0,0,0,2,1,3,1])
data = array([1,1,1,8,1,1,1])
matrix = coo_matrix((data, (row,col)), shape=(4,4))
print(matrix)
print(matrix.todense())
  (0, 0)    1
  (0, 0)    1
  (0, 0)    1
  (0, 2)    8
  (1, 1)    1
  (3, 3)    1
  (1, 1)    1
[[3 0 8 0]
 [0 2 0 0]
 [0 0 0 0]
 [0 0 0 1]]

Note:csr_matrix总是返回稀疏矩阵，而不会返回一维向量。即使csr_matrix([2,3])也返回矩阵。
稀疏矩阵大小

csr = csr_matrix([[1, 5], [4, 0], [1, 3]])
print(csr.todense())    #todense()之后是<class 'numpy.matrixlib.defmatrix.matrix'>
print(csr.shape)
print(csr.shape[1])
[[1 5]
 [4 0]
 [1 3]]
(3, 2)
2

稀疏矩阵下标存取slice

print(csr)
  (0, 0)    1
  (0, 1)    5
  (1, 0)    4
  (2, 0)    1
  (2, 1)    3
print(csr[0]) #<class 'scipy.sparse.csr.csr_matrix'>
  (0, 0)    1
  (0, 1)    5
print(csr[1,1])
1
print(csr[0,0])
0
for c in csr:    #每次读取csr中的一行 type(c) <class 'scipy.sparse.csr.csr_matrix'>
    print(c)
    break
  (0, 0)    1
  (0, 1)    5

csr_mat = csr_matrix([1, 5, 0])
print(csr_mat.todense())
# print(type(csr_mat.nonzero()))  #<class 'tuple'>
for row, col in csr_mat.nonzero():
    print(row, col, csr_mat[row, col])
[[1 5 0]]
0 0 1
0 1 5

将稀疏矩阵横向或者纵向合并

from scipy.sparse import coo_matrix, vstack

csr = csr_matrix([[1, 5, 5], [4, 0, 6], [1, 3, 7]])
print(csr.todense())
[[1 5 5]
 [4 0 6]
 [1 3 7]]
csr2 = csr_matrix([[3, 0, 9]])
print(csr2.todense())
[[3 0 9]]
print(vstack([csr, csr2]).todense())
[[1 5 5]
 [4 0 6]
 [1 3 7]
 [3 0 9]]

Note:如果合并数据形式不一样，不能合并。一个矩阵中的数据格式必须是相同的。

diags函数建立稀疏的对角矩阵

sparce矩阵的读取
可以像常规矩阵一样通过下标读取。也可以通过getrow(i)，gecol(i)读取特定的列或者特定的行，以及nonzero()读取非零元素的位置。

对于大多数（似乎只处了coo之外）稀疏矩阵的存储格式，都可以进行slice操作，比如对于csc，csr。也可以进行arithmeticoperations，矩阵的加减乘除，速度很快。

取矩阵的指定列数

sub = matrix.getcol(1)    #'coo_matrix' object does not support indexing，不能使用matrix[1]
print(sub)
  (1, 0)    2
sub = matrix.todense()[:,[1,2]]    #常规矩阵取指定列print(sub)
[[0 8]
 [2 0]
 [0 0]
 [0 0]]

稀疏矩阵点积计算

A = csr_matrix([[1, 2, 0], [0, 0, 3]])
print(A.todense())
[[1 2 0]
 [0 0 3]]
v = A.T
print(v.todense())
[[1 0]
 [2 0]
 [0 3]]
d = A.dot(v)
print(d)
  (0, 0)    5
  (1, 1)    9

A = lil_matrix([[1, 2, 0], [0, 0, 3], [4, 0, 5]])
v = array([1, 0, -1])
s = datetime.datetime.now()
for i in range(100000):
    d = A.dot(v)    #这里v是一个ndarray
print(datetime.datetime.now() - s)

计算时间：
bsr:0:00:01.666072
coo:1.04
csc:0.93
csr:0.90
dia:1.06
dok:1.57
lil:11.37
故推荐用csr计算点积

csr_mat1 = csr_matrix([1, 2, 0])
csr_mat2 = csr_matrix([1, 0, -1])
similar = (csr_mat1.dot(csr_mat2.transpose()))   #这里csr_mat2也是一个csr_matrix
print(type(similar))
print(similar)
print(similar[0, 0])
<class 'scipy.sparse.csr.csr_matrix'>
  (0, 0)    1
1

scipy稀疏矩阵在文件中的读取（读取和保存稀疏矩阵）

mmwrite(target, a[, comment, field, precision]) Writes the sparse or dense array a to a Matrix Market formatted file.

mmread(source) Reads the contents of a Matrix Market file ‘filename’ into a matrix.<class 'scipy.sparse.coo.coo_matrix'>

mminfo(source) Queries the contents of the Matrix Market file ‘filename’ to extract size and storage.

def save_csr_mat(
        item_item_sparse_mat_filename=r'.\datasets\lastfm-dataset-1K\item_item_csr_mat.mtx'):
    random.seed(10)
    raw_user_item_mat = random.randint(0, 6, (3, 2))
    d = csr_matrix(raw_user_item_mat)
    print(d.todense())
    print(d)
    mmwrite(item_item_sparse_mat_filename, d)
    print("item_item_sparse_mat_file information: ")
    print(mminfo(item_item_sparse_mat_filename))
    k = mmread(item_item_sparse_mat_filename)
    print(k.todense())

[[1 5]
 [4 0]
 [1 3]]  

  (0, 0)    1
  (0, 1)    5
  (1, 0)    4
  (2, 0)    1
  (2, 1)    3

item_item_sparse_mat_file information: 
(3, 2, 5, 'coordinate', 'integer', 'general')

[[1 5]
 [4 0]
 [1 3]]

保存的文件中的内容：
%%MatrixMarket matrix coordinate integer general
%
3 2 5
1 1 1
1 2 5
2 1 4
3 1 1
3 2 3

Note:保存的文件拓展名应为.mtx

[scipy-ref-0.14.0 -  Matrix Market files]

皮皮blog

一种比较省内存的稀疏矩阵Python存储方案

    推荐系统中经常需要处理类似user_id, item_id, rating这样的数据，其实就是数学里面的稀疏矩阵，scipy中提供了sparse模块来解决这个问题。
    但scipy.sparse有很多问题不太合用：1、不能很好的同时支持data[i, ...]、data[..., j]、data[i, j]快速切片；2、由于数据保存在内存中，不能很好的支持海量数据处理。
    要支持data[i, ...]、data[..., j]的快速切片，需要i或者j的数据集中存储；同时，为了保存海量的数据，也需要把数据的一部分放在硬盘上，用内存做buffer。这里的解决方案比较简单，用一个类Dict的东西来存储数据，对于某个i（比如9527），它的数据保存在dict['i9527']里面，同样的，对于某个j（比如3306），它的全部数据保存在dict['j3306']里面，需要取出data[9527, ...]的时候，只要取出dict['i9527']即可，dict['i9527']原本是一个dict对象，储存某个j对应的值，为了节省内存空间，我们把这个dict以二进制字符串形式存储 。
    采用类Dict来存储数据的另一个好处是你可以随便用内存Dict或者其他任何形式的DBM，甚至传说中的Tokyo Cabinet. [http://blogread.cn/it/article/1229]

from: http://blog.csdn.net/pipisorry/article/details/41762945

ref:sparse模块的官方document

http://blog.sina.com.cn/s/blog_6a90ae320101aavg.html