庞果网之寻找直方图中面积最大的矩形
题目详情
【解析】
使用一个栈来保存输入柱状条,每个柱状条包含两个信息:(1)柱状条的高度(height);(2)柱状条的宽度(width) 。初始宽度均为单位宽度1。
在随后的入栈和出栈中随时更改柱状条的宽度。
(1)当入栈柱状条的高度大于栈顶柱状条的高度或者栈为空时,柱状条入栈;如图1
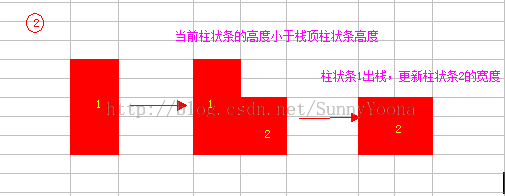
(2)当入栈柱状条的高度小于栈顶柱状条的高度时,柱状条出栈,同时计算出栈的柱状条的面积,更新最大矩形面积。同时更新当前柱状条的宽度。如图2
(3)当入栈柱状条的高度等于栈顶柱状条的高度时,柱状条出栈,更新当前柱状条宽度。如图3
(4)如果最后栈不空,只剩高度递增的柱状条。一个一个出栈,更新最大矩形面积。每一个柱状条出栈都要更新前一个柱状条的宽度。如图4
写的不好,勿喷。
【代码】
/*********************************
* 日期:2013-11-24
* 作者:SJF0115
* 题号: 寻找直方图中面积最大的矩形
* 来源:http://hero.pongo.cn/Question/Details?ID=58&ExamID=56
* 结果:AC
* 来源:庞果网
* 总结:
**********************************/
#include<iostream>
#include<stack>
#include<vector>
#include<stdio.h>
#include<malloc.h>
using namespace std;
typedef struct Rec{
int height;
int width;
}Rec;
int LargestRectangleArea(vector<int> &height){
int Max = 0,i;
int n = height.size();
//容错处理
if(n <= 0){
return 0;
}
Rec *rec = (Rec*)malloc(sizeof(Rec)*n);
stack<Rec> stack;
//初始化
for(i = 0;i < n;i++){
rec[i].height = height[i];
rec[i].width = 1;
}
for(i = 0;i < n;i++){
int h = rec[i].height;
//如果栈空或者当前高度大于栈顶的矩形高度的时候就压入栈
if(stack.empty() || h > stack.top().height){
stack.push(rec[i]);
}
else{
int preWidth = 0;
//小于栈顶的矩形高度就弹出栈,更新最大的矩形面积
while(!stack.empty() && h < stack.top().height){
rec[i].width += stack.top().width;
//当前面积
int currentMax = stack.top().height * (stack.top().width + preWidth);
//更新最大值
if(Max < currentMax){
Max = currentMax;
}
preWidth += stack.top().width;
//出栈
stack.pop();
}
//等于栈顶的矩形高度
while(!stack.empty() && h == stack.top().height){
rec[i].width += stack.top().width;
stack.pop();
}
//栈空
if(stack.empty() || h > stack.top().height){
stack.push(rec[i]);
}
}
}
//最后栈中只剩递增的序列
int width = 0;
while(!stack.empty()){
int currentMax = stack.top().height * (stack.top().width + width);
if(currentMax > Max){
Max = currentMax;
}
width += stack.top().width;
stack.pop();
}
return Max;
}
int main(){
int i,n,Max,num;
while(scanf("%d",&n) != EOF){
vector<int> height;
for(i = 0;i < n;i++){
scanf("%d",&num);
height.push_back(num);
}
Max = LargestRectangleArea(height);
printf("%d\n",Max);
}
return 0;
}
【方法二】
【解析】
设柱状图为非负整数数组A, 则最大矩形的高度必定是数组的某一项height[i]。
设f(i) 为以数组第i项的高度为矩形高度时矩形的最大宽度,则最大矩形为max{f(i)*height[i]} (0 <= i < n)
f(i)本身无法动态规划,但若将f(i)拆成左右两部分,则很容易动态规划求解
令left(i)为以数组第i项为矩形高度时矩形左侧最大宽度,
right(i)为以数组第i项为矩形高度时矩形右侧最大宽度,
则f(i) = left(i) + right(i) - 1
【代码】
/*********************************
* 日期:2013-11-25
* 作者:SJF0115
* 题号: 寻找直方图中面积最大的矩形
* 来源:http://hero.pongo.cn/Question/Details?ID=58&ExamID=56
* 结果:AC
* 来源:庞果网
* 总结:
**********************************/
#include <stdio.h>
int left[100001],right[100001];
int largestRectangleArea(const int *height,int n) {
int Max = 0,i,j;
//容错处理
if(height == NULL || n <= 0){
return 0;
}
left[0] = 1;
right[n-1] = 1;
//以数组第i项为矩形高度时矩形左侧最大宽度
for(i = 1;i < n;i++){
//初始为单位宽度1
left[i] = 1;
for(j = i-1;j >= 0;){
if(height[i] <= height[j]){
left[i] += left[j];
//跳到下一个比较对象
j -= left[j];
}
else{
break;
}
}
//printf("第%d项左最大宽度:%d\n",i+1,left[i]);
}
//以数组第i项为矩形高度时矩形右侧最大宽度
for(i = n-2;i >= 0;i--){
//初始为单位宽度1
right[i] = 1;
for(j = i+1;j < n;){
if(height[i] <= height[j]){
right[i] += right[j];
//跳到下一个比较对象
j += right[j];
}
else{
break;
}
}
//printf("第%d项右最大宽度:%d\n",i+1,right[i]);
}
for(i = 0;i < n;i++){
int currentMax = (left[i] + right[i] - 1) * height[i];
if(Max < currentMax){
Max = currentMax;
}
}
return Max;
}
//start 提示:自动阅卷起始唯一标识,请勿删除或增加。
int main()
{
int height[] = {1,2,3,4,3,4,3,2,1};
int max = largestRectangleArea(height,9);
printf("%d\n",max);
return 0;
}
//end //提示:自动阅卷结束唯一标识,请勿删除或增加。
【测试数据】
{1,2,3,4,3,4,3,2,1} 结果: 15
{3,4,5,6} 结果:12
{2,1,2,1,2,1} 结果:6
{2,1,5,6,2,3}结果:10
{2, 1, 4, 5, 1, 3, 3, 1, 2} 结果:9