【算法导论】最大二分匹配
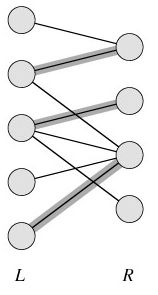
最大二分匹配问题在现实生活中比较普遍,常常出现在任务分配上。例如,有5个员工,4个不同的任务,而不同员工能够完成不同或相同的任务。也就是说,有的员工只会做这个任务,有的员工会做那个任务,有的员工会做一些任务。图解如下:左边代表员工,右边代表任务,连线代表有能力完成。
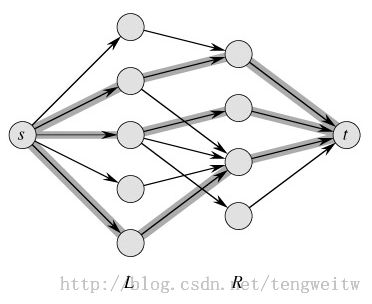
我们的问题是合理安排员工,尽可能地完成最多的任务数。上图中阴影部分为一种最好的分配方式。前一篇文章中,我们介绍了最大流问题,在这里我们可以将最大二分匹配问题转变成最大流问题。具体如下图所示:
其中每条边的最大流量限制为1,因此要求能完成的最大任务数,相当于求转变后的网络的最大流,而最大流问题在前面已经提及。
具体的程序实现如下:
#include<stdio.h>
#define N 11 //顶点数
/********************************************************\
函数功能:从残留网络中找到从源点s到汇点t的增广路径
输入:残留网络矩阵、记录前一顶点的矩阵
输出:0表示未找到路径,1表示找到了路径
\********************************************************/
int search(int dist1[N][N],int vertex[N])
{
int queue[20]={-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1};//初始化,-1作为标记
int flag[N]={0};//标记顶点是否被访问过
int front=0;//队列头指针
int rear=0;//队列尾指针
int temp=0;
int i;
queue[rear]=0;//将源点入队列
flag[0]=1;
rear++;
while(queue[front]!=-1)//队列不为空
{
temp=queue[front];//取队头元素
for(i=0;i<N;i++)
if(dist1[temp][i]!=0&&flag[i]==0)//广度搜索法
{
queue[rear++]=i;//入队
flag[i]=1;
vertex[i]=temp;//标记当前节点的上一个节点
if(i==10)//找到汇点后就不用再寻找了
return 1;
}
front++;
if(front==N)//找完所有顶点后停止寻找
break;
}
if(queue[rear-1]!=10)//没有找到路径到汇点
return 0;
return 1;
}
/**************************************************************************\
函数功能:修改残余网络矩阵和原始流网络矩阵
输入:原始流网络矩阵、残留网络矩阵、记录前一顶点的矩阵、源点和汇点,最大流值
输出:0表示未找到路径,1表示找到了路径
\***************************************************************************/
int modify(int dist[N][N],int dist1[N][N],int vertex[N],int s,int t,int flow)
{
int i,j;
int min=10000;//记录找到的路径所能通过的最大流
i=vertex[t];
j=t;
while(j!=s)//寻找路径所含边的最大流量值中的最小值
{
if(dist1[i][j]<min)
min=dist1[i][j];
j=i;
i=vertex[i];
}
i=vertex[t];
j=t;
flow=min;//记录最大流量
while(j!=s)
{
if(dist1[i][j]>0)//更改残余图
dist1[j][i]=dist1[i][j];
dist1[i][j]=dist1[i][j]-min;
dist[i][j]=dist[i][j]+min-dist[j][i];//更改原始流网路
if(dist[i][j]<0)
{
dist[j][i]=-dist[i][j];
dist[i][j]=0;
}
j=i;
i=vertex[i];
}
printf("原始流网络矩阵:\n");
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
printf("%d ",dist[i][j]);
printf("\n");
}
printf("残留网络矩阵:\n");
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
printf("%d ",dist1[i][j]);
printf("\n");
}
return flow;
}
void FordFulkerson(int dist[N][N],int dist1[N][N])
{
int vertex[N]={0};//初始化
int flow=0;
while(search(dist1,vertex)==1)//当能找到增广路径时
{
flow=flow+modify(dist,dist1,vertex,0,10,0);
printf("\n");
}
printf("最大流为%d \n",flow);
}
void main()
{
int dist1[N][N]={{0,1,1,1,1,1,0,0,0,0,0},
{0,0,0,0,0,0,1,0,0,0,0},
{0,0,0,0,0,0,1,0,1,0,0},
{0,0,0,0,0,0,0,1,1,1,0},
{0,0,0,0,0,0,0,0,1,0,0},
{0,0,0,0,0,0,0,0,1,0,0},
{0,0,0,0,0,0,0,0,0,0,1},
{0,0,0,0,0,0,0,0,0,0,1},
{0,0,0,0,0,0,0,0,0,0,1},
{0,0,0,0,0,0,0,0,0,0,1},
{0,0,0,0,0,0,0,0,0,0,0}};
int dist[N][N]={0};//初始的流网络为0
FordFulkerson(dist,dist1);
}
程序结果为最大流为3,与前面的图解一致,但是我们发现结果与图解的不同,这说明最大二分匹配可以有不同的解即有不同的分配方案。
注:如果程序出错,可能是使用的开发平台版本不同,请点击如下链接: 解释说明
原文:http://blog.csdn.net/tengweitw/article/details/17848773
作者:nineheadedbird