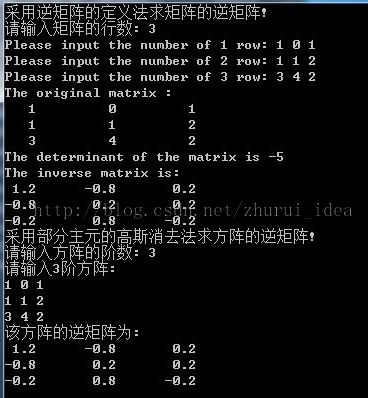
矩阵求逆c++实现

         高斯消元法可以用来找出一个可逆矩阵的逆矩阵。设A 为一个N * N的矩阵，其逆矩阵可被两个分块矩阵表示出来。将一个N * N单位矩阵 放在A 的右手边，形成一个N * 2N的分块矩阵B = [A,I] 。经过高斯消元法的计算程序后，矩阵B 的左手边会变成一个单位矩阵I ，而逆矩阵A ^(-1) 会出现在B 的右手边。假如高斯消元法不能将A 化为三角形的格式，那就代表A 是一个不可逆的矩阵。应用上，高斯消元法极少被用来求出逆矩阵。高斯消元法通常只为线性方程组求解。

 //********************************
//*** 求任何一个实矩阵的逆***
//********************************
#include "stdafx.h"
#include <math.h>
#include <malloc.h>
#include <iostream> 
#include <iomanip>
using namespace std; 
#define  N  10                //定义方阵的最大阶数为10
//函数的声明部分
float MatDet(float *p, int n);                    //求矩阵的行列式
float Creat_M(float *p, int m, int n, int k);    //求矩阵元素A(m, n)的代数余之式
void print(float *p, int n);                    //输出矩阵n*n
bool Gauss(float A[][N], float B[][N], int n);    //采用部分主元的高斯消去法求方阵A的逆矩阵B
int main()
{
    float *buffer, *p;            //定义数组首地址指针变量
    int row, num;                //定义矩阵的行数和矩阵元素个数
    int i, j;
    float determ;                //定义矩阵的行列式
    float a[N][N], b[N][N];
    int n;
    cout << "采用逆矩阵的定义法求矩阵的逆矩阵!\n";
    cout << "请输入矩阵的行数: ";
    cin >> row;
    num = 2 * row * row;
    buffer = (float *)calloc(num, sizeof(float));        //分配内存单元
    p = buffer;
    if (NULL != p)
    {
        for (i = 0; i < row; i++)
        {
            cout << "Please input the number of " << i+1 << " row: ";
            for (j = 0; j < row; j++)
            {
                cin >> *p++;
            }
        }
    }
    else
    {
        cout << "Can't distribute memory\n";
    }
    cout << "The original matrix : \n";
    print(buffer, row);                //打印该矩阵
    
    determ = MatDet(buffer, row);    //求整个矩阵的行列式
    p = buffer + row * row;
    if (determ != 0)
    {
        cout << "The determinant of the matrix is " << determ << endl;
        for (i = 0; i < row; i++)    //求逆矩阵
        {
            for (j = 0; j < row; j++)
            {
                *(p+j*row+i) = Creat_M(buffer, i, j, row)/determ;
            }
        }
        cout << "The inverse matrix is: " << endl;
        print(p, row);                //打印该矩阵
    } 
    else
    {
        cout << "The determinant is 0, and there is no inverse matrix!\n";
    }
    free(buffer);        //释放内存空间
    cout << "采用部分主元的高斯消去法求方阵的逆矩阵!\n";
    cout << "请输入方阵的阶数: ";
    cin >> n;
    cout << "请输入" << n << "阶方阵: \n";
    //输入一个n阶方阵
    for (i = 0; i < n; i++)
    {
        for (j = 0; j < n; j++)
        {
            cin >> a[i][j];
        }
    }
    //运用高斯消去法求该矩阵的逆矩阵并输出
    if (Gauss(a, b, n))
    {
        cout << "该方阵的逆矩阵为: \n";
        for (i = 0; i < n; i++)
        {
            cout << setw(4);
            for (j = 0; j < n; j++)
            {
                cout << b[i][j] << setw(10);
            }
            cout << endl;
        }
    }    
	getchar();
    return 0;
}
//-----------------------------------------------
//功能: 求矩阵(n*n)的行列式
//入口参数: 矩阵的首地址，矩阵的行数
//返回值: 矩阵的行列式值
//----------------------------------------------
float MatDet(float *p, int n)
{
    int r, c, m;
    int lop = 0;
    float result = 0;
    float mid = 1;
    if (n != 1)
    {
        lop = (n == 2) ? 1 : n;            //控制求和循环次数,若为2阶，则循环1次，否则为n次
        for (m = 0; m < lop; m++)
        {
            mid = 1;            //顺序求和, 主对角线元素相乘之和
            for (r = 0, c = m; r < n; r++, c++)
            {
                mid = mid * (*(p+r*n+c%n));
            }
            result += mid;
        }
        for (m = 0; m < lop; m++)
        {
            mid = 1;            //逆序相减, 减去次对角线元素乘积
            for (r = 0, c = n-1-m+n; r < n; r++, c--)
            {
                mid = mid * (*(p+r*n+c%n));
            }
            result -= mid;
        }
    }
    else 
        result = *p;
    return result;
}
//----------------------------------------------------------------------------
//功能: 求k*k矩阵中元素A(m, n)的代数余之式
//入口参数: k*k矩阵的首地址，矩阵元素A的下标m,n,矩阵行数k
//返回值: k*k矩阵中元素A(m, n)的代数余之式
//----------------------------------------------------------------------------
float Creat_M(float *p, int m, int n, int k)
{
    int len;
    int i, j;
    float mid_result = 0;
    int sign = 1;
    float *p_creat, *p_mid;
    len = (k-1)*(k-1);            //k阶矩阵的代数余之式为k-1阶矩阵
    p_creat = (float*)calloc(len, sizeof(float)); //分配内存单元
    p_mid = p_creat;
    for (i = 0; i < k; i++)
    {
        for (j = 0; j < k; j++)
        {
            if (i != m && j != n) //将除第i行和第j列外的所有元素存储到以p_mid为首地址的内存单元
            {
                *p_mid++ = *(p+i*k+j);
            }
        }
    }
    sign = (m+n)%2 == 0 ? 1 : -1;    //代数余之式前面的正、负号
    mid_result = (float)sign*MatDet(p_creat, k-1);
    free(p_creat);
    return mid_result;
}
//-----------------------------------------------------
//功能: 打印n*n矩阵
//入口参数: n*n矩阵的首地址,矩阵的行数n
//返回值: 无返回值
//-----------------------------------------------------
void print(float *p, int n)
{
    int i, j;
    for (i = 0; i < n; i++)
    {
        cout << setw(4);
        for (j = 0; j < n; j++)
        {
            cout << setiosflags(ios::right) << *p++ << setw(10);
        }
        cout << endl;
    }
}
//------------------------------------------------------------------
//功能: 采用部分主元的高斯消去法求方阵A的逆矩阵B
//入口参数: 输入方阵，输出方阵，方阵阶数
//返回值: true or false
//-------------------------------------------------------------------
bool Gauss(float A[][N], float B[][N], int n)
{
    int i, j, k;
    float max, temp;
    float t[N][N];                //临时矩阵
    //将A矩阵存放在临时矩阵t[n][n]中
    for (i = 0; i < n; i++)        
    {
        for (j = 0; j < n; j++)
        {
            t[i][j] = A[i][j];
        }
    }
    //初始化B矩阵为单位阵
    for (i = 0; i < n; i++)        
    {
        for (j = 0; j < n; j++)
        {
            B[i][j] = (i == j) ? (float)1 : 0;
        }
    }
    for (i = 0; i < n; i++)
    {
        //寻找主元
        max = t[i][i];
        k = i;
        for (j = i+1; j < n; j++)
        {
            if (fabs(t[j][i]) > fabs(max))
            {
                max = t[j][i];
                k = j;
            }
        }
        //如果主元所在行不是第i行，进行行交换
        if (k != i)
        {
            for (j = 0; j < n; j++)
            {
                temp = t[i][j];
                t[i][j] = t[k][j];
                t[k][j] = temp;
                //B伴随交换
                temp = B[i][j];
                B[i][j] = B[k][j];
                B[k][j] = temp; 
            }
        }
        //判断主元是否为0, 若是, 则矩阵A不是满秩矩阵,不存在逆矩阵
        if (t[i][i] == 0)
        {
            cout << "There is no inverse matrix!";
            return false;
        }
        //消去A的第i列除去i行以外的各行元素
        temp = t[i][i];
        for (j = 0; j < n; j++)
        {
            t[i][j] = t[i][j] / temp;        //主对角线上的元素变为1
            B[i][j] = B[i][j] / temp;        //伴随计算
        }
        for (j = 0; j < n; j++)        //第0行->第n行
        {
            if (j != i)                //不是第i行
            {
                temp = t[j][i];
                for (k = 0; k < n; k++)        //第j行元素 - i行元素*j列i行元素
                {
                    t[j][k] = t[j][k] - t[i][k]*temp;
                    B[j][k] = B[j][k] - B[i][k]*temp;
                }
            }
        }
    }
	getchar();
    return true;
}

实验结果：