算法入门之队列的链式表示
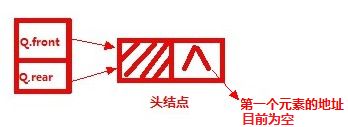
和线性类似,队列也可以有俩种存储表示。一个链队列需要都两个分别指向队头和队尾的指针(分别称为头指针和尾指针)才能唯一确定。为了操作方便,除了以上两个指针外,我们还为对列添加一个头结点。初始化是头指针和尾指针都指向头结点,因此,当头指针和尾指针均指向头结点时,此队列为空。
1. 定义存储结构:
typedef struct QNode
{
QElemType data; //存放的数据,称为数据域
struct QNode *next; //存放下一个的地址,称为指针域
} QNode, *QueuePtr;
typedef struct
{
QueuePtr front; //队头指针
QueuePtr rear; //队尾指针
} LinkQueue;
2. 构建一个空队列Q:
Status InitQueue(LinkQueue &Q)
{
Q.front = Q.rear = (QueuePtr) malloc(sizeof(QNode)); //向系统申请分配内存空间
if (!Q.front) //如果内存分配失败,程序异常退出
exit(OVERFLOW);
Q.front->next = NULL;
return OK;
}
结果如下图:
3.进队:让e进队,作为新的对尾:
Status EnQueue(LinkQueue &Q, QElemType e)
{
QueuePtr p = (QueuePtr) malloc(sizeof(QNode)); //生成一个新的结点p
if (!p) //如果内存分配失败,如果内存分配失败,程序异常退出
exit(OVERFLOW);
p->data = e; //将要进队列的值放与p的数据域data上
p->next = NULL; //p下一个为空
Q.rear->next = p; //原本的队尾rear的指针域next中存放p的地址
Q.rear = p; //结点p作为新的队尾
return OK;
}
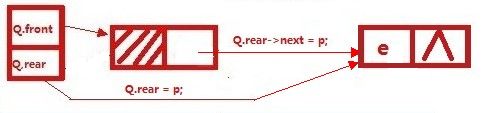
结果如下图:
再e1入队列:
4.出队:若队列不为空,则删除Q的对头元素,用x返回其值:
Status DeQueue(LinkQueue &Q, QElemType &x)
{
if (Q.front == Q.rear) //若队列为空,返回ERROR。
return ERROR;
QueuePtr p = Q.front->next; //队头结点赋给p
x = p->data; //队头的数据域赋予x
Q.front->next = p->next; //p的指针域赋予队头的指针域
if (Q.rear == p) //若该队列只有一个元素,则该元素出队列后,队列为空
Q.rear = Q.front;
free(p); //释放临时结点p
return OK;
}
结果如下图:
5.队头:获得队头的值,同样用x返回其值:
Status QueueHead(LinkQueue Q, QElemType &x) { if(QueueEmpty(Q)) return ERROR; QueuePtr p=Q.front->next;//注意这里是QueuePtr p=Q.front->next,而不是QueuePtr p=Q.front x=p->data; return OK; }
6.判读队列是否为空:Status QueueEmpty(LinkQueue Q) { return Q.front == Q.rear; }7.销毁队列:
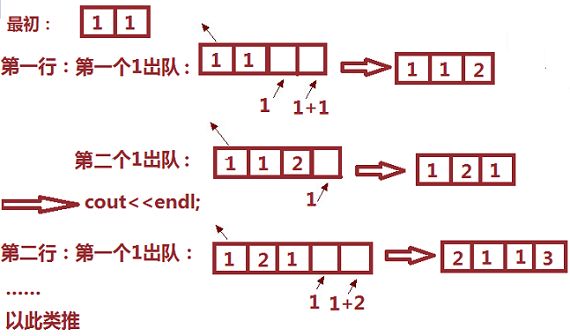
Status DestroyQueue(LinkQueue &Q){ while(Q.front){ Q.rear = Q.front->next; //队尾在这里作为一个“中介”,暂时存放第二个结点 free(Q.front); //销毁队头 Q.front = Q.rear; //原先的第二个结点作为新的队头 } return OK; }8.队列实例运用之杨辉三角如下图:
Status YhTriangle(LinkQueue &Q, int n){ EnQueue(Q,1); EnQueue(Q,1); int i = 2; //用于控制打印数字前的缩进 bool flag = 0; //用于区别同一行的两个"1" while(n >= 2){ //前n-1行 QElemType e; DeQueue(Q,e); if(flag && e == 1){ //若出队的是第二个"1",再进"1"。 flag = 0; EnQueue(Q,1); cout<<setw(4)<<e<<endl; --n; } else{ if(e == 1){ //若出队的是第一个"1",再进"1"。 for(int j = 0; j < n-i + 1; j++) cout<<setw(2)<<" "; flag = 1; EnQueue(Q,1); } cout<<setw(4)<<e<<" "; QElemType e1 = e + Q.front->next->data; //若出队的是一行中的第一个"1"或者非"1",使其与队头的和入队。 EnQueue(Q,e1); } } while(!QueueEmpty(Q)){ //最后一行 QElemType e2; DeQueue(Q,e2); cout<<setw(4)<<e2<<" "; } return OK; }图示:
注意:队头是Q.front->next;