【白话系列】最近公共祖先

【序言】

        说到最近公共祖先，应该是树论中一个比较重要的话题吧。一般来说，在遇到求最近公共祖先的时候，会有三种常见的做法：对于简单的模拟题——直接模拟就好了；对于大题目中的求最近公共祖先的小桥段——用tarjan来求，因为好打不容易错；对于特意考察最近公共祖先，并且数据范围比较大的时候——用倍增算法，省空间还是硬道理。至于还有的通过变形将最近公共祖先问题化为区域最小值问题来做，性价比并不高，如果你硬是想知道，可以百度一下：“LCA问题转RMQ问题的ST算法”。

【什么是最近公共祖先？】

        最近公共祖先简称LCA，以下用LCA代替。

        不要期望我解释什么是LCA嗯，我知道你知道！（哼，这只是走个过程而已！）好吧，如果你真不知道，我也无法解释，请看：

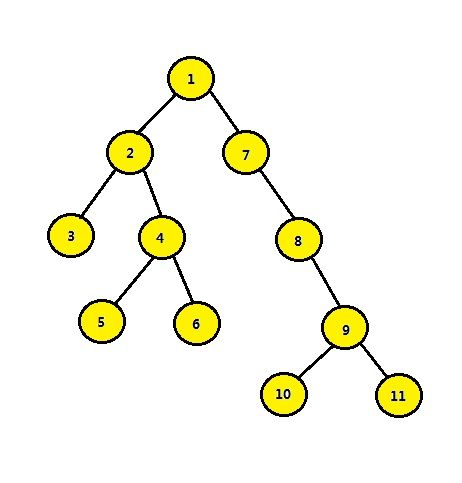
        LCA（3 4）=2   LCA（3 2）=2    LCA（6 10）=1   LCA（5 6）=4

        我想你已经知道了，LCA就是两个节点前往根节点的两条路径第一次交汇的那个节点，也就是距离它们最近的祖先，而且是公共的祖先，哈哈！

【模拟的做法】

        还记得刚才的那句话么！“LCA就是两个节点前往根节点的两条路径第一次交汇的那个节点”！那么模拟法岂不是太显而易见了吗？直接从要求的一个点开始，不停地往父亲走，把它经过的点都标记为已访问，直到不能再走为止，再从另一个点开始，不停往父亲走，并检查它经过的点是不是曾今被访问过，如果是，那么这个点就是它们的最近公共祖先。如果你要问我为什么，我真的会很难过的，真的。

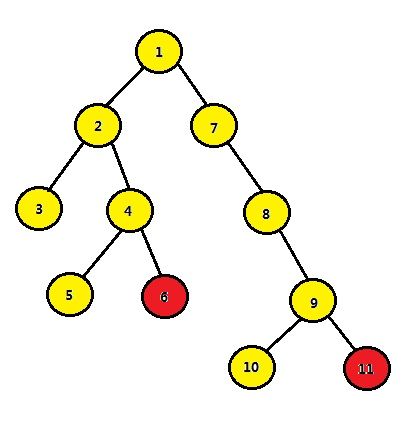
        注意：模拟法在马虎的时候也是容易出错误的，记住一个完整的小流程是“先标记再往上走”而不是“先往上走再标记”，这并不一样，如上图，若是找2 与 3的LCA，先模拟2的路径，如果“先标记再往上走”那么走完以后被标记的有1与2，如果“先往上走再标记”，那么被标记的就只有1，显然这是不可取的，因为最后求出来的LCA就变成1号节点了！这是常见的一个小错误，当然，对于另外一个节点，也应该“先检查再往上走”，因为它自己本身这个节点就有可能是它们的LCA。切记啊切记，这样的错误不能出现了啊！！

【tarjan的做法】

        刚才我们一直在做的都是解决两个节点的LCA是哪个节点，tarjan固然也是解决这样的问题的，只不过它可以更加快速，在线性的时间阶内求出所有的询问。tarjan到底是怎么做的？请往下看。

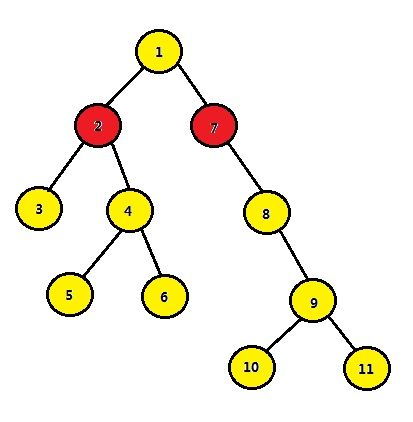
        首先，我们来想想这样一个问题：在如图的这棵树中，LCA为1号节点的有哪些节点对？也许你觉得这个问题实在是太简单了，一眼就可以看出，只要在1号节点的左子树随便找一个节点，再与从1号节点的右子树中随便找出的一个节点组成节点对，那么它们的LCA一定是1号节点。为什么？显然可得，不需要任何理由，感觉就是硬道理。

        那么我们可不可以抽象一样：若两节点分别分布于某节点的左右子树，那么该节点为其LCA。凭感觉得出的定理还是有一定的问题，因为并没有考虑到一个节点自己就是LCA的情况，所以我们对定理进行补充：若某节点是两节点的祖先之一，且这两节点并不分布于该节点的一棵子树中，那么该节点即为两节点的LCA。这就是Tarjan算法赖以生存的基础。

        先不说Tarjan算法，就说刚才我们得到的那个显而易见的定理，你有没有什么思路呢？你有没有想到，可以先预处理出所有询问的LCA，然后再一起回答呢？

        对于很多组的询问，我先确定一个LCA，就假设它是根节点1好了，然后再去检查所有询问，看是否满足刚才的定理，不满足就忽视，满足就赋值，全部弄完，再去假设2号节点是LCA，再去访问一遍……有没有发现这个方法无比的通俗与直观？但是！你要怎么知道一个节点是在左子树、右子树还是都不在呢？我想你只能遍历一棵树，那么，好像这个方法也并没有比直接模拟法好多少，但是，不要放弃，因为Tarjan就没有放弃。

        我们觉得刚才的算法不妥，是因为多次遍历的代价实在是太大了，但是细心一点，我们便可以发现，若一个点的父亲会被某个点遍历到，那么该点也会被那个点遍历到，也就是说一个点只需要被遍历一遍即可，因为遍历信息是可以传递的！

tarjan算法流程：

        procedure dfs（i）；

        begin

            设置i号节点的祖先为i

            若i的左子树不为空，dfs（i-左子树）；

            若i的右子树不为空，dfs（i-右子树）；

            访问每一条与i相关的询问

                    若另一个节点已经被访问过，则输出另一个节点当前的祖先

            标记i为已经访问，将所有i的孩子包括i本身的祖先改为i的父亲

        end；

STEP 1
节点	1	2	3	4	5	6	7	8
祖先	1	2	3

STEP 2
节点	1	2	3	4	5	6	7	8
祖先	1	2	2

STEP 3
节点	1	2	3	4	5	6	7	8
祖先	1	2	2	4	5

STEP 4
节点	1	2	3	4	5	6	7	8
祖先	1	2	2	4	4

STEP 5
节点	1	2	3	4	5	6	7	8
祖先	1	2	2	4	4	6

STEP 6
节点	1	2	3	4	5	6	7	8
祖先	1	2	2	4	4	4

STEP 7
节点	1	2	3	4	5	6	7	8
祖先	1	2	2	2	2	2

STEP 8
节点	1	2	3	4	5	6	7	8
祖先	1	1	1	1	1	1

STEP 9
节点	1	2	3	4	5	6	7	8
祖先	1	1	1	1	1	1	7

STEP 10
节点	1	2	3	4	5	6	7	8
祖先	1	1	1	1	1	1	7	8

STEP 11
节点	1	2	3	4	5	6	7	8
祖先	1	1	1	1	1	1	7	7

STEP 12
节点	1	2	3	4	5	6	7	8
祖先	1	1	1	1	1	1	1	1

STEP 13
节点	1	2	3	4	5	6	7	8
祖先	1	1	1	1	1	1	1	1

        大致流程如上所示，我们可以惊喜的发现，当我们在检查一个节点的询问情况的时候，若与询问相关的另一个节点已经被访问，那么以另一个节点当前的祖先为祖先，这两个节点一定是满足我们凭感觉得到的那个定理的，也就是说，这个祖先一定是最近公共祖先。

        为什么？因为这个神奇的逻辑顺序，就是这么这么巧，没有任何问题。

        如果你还是有点懵懂，按照Tarjan的算法流程再将这十来幅手动模拟的图片看上几遍，你一定就会懂的。

【倍增的做法】

        倍增来做LCA应该是比Tarjan更容易理解的，因为它更加直观，更加符合人模拟的思维。

还记得前面说的模拟的方法来做LCA吗？其实倍增可以算作是模拟算法在往上走的过程中的一个优化，让我们不是每次走一步，而是尽可能一次走很多步。

        ps、倍增是什么？详情请看http://blog.csdn.net/jarjingx/article/details/8180560 

        既然已经知道了倍增，那么就不赘述了，直接上算法流程。

        1、预处理出每个节点的深度

        2、读取一组询问，对于两个节点，先跳到同一深度

        3、判断当前两节点所在的节点是否为同一节点，是则其为LCA，否则继续下一步

        4、从大往小进行检查，……8步、4步、2步、1步……，若跳后节点不一致，则可以跳，若节点一致，则不跳

        5、两节点所在的点的父亲节点即为LCA

若询问为 6与11的LCA：

        step1、比较深度大小

        step2、深度不一致，跳至同一深度

        step3、6跳8步与9跳8步不满足要求

                       6跳4步与9跳4步步满足要求

                       6跳2步与9跳2步满足要求

        step4、2跳1步与7跳1步不满足要求

        step5、2和7共同的父亲1为其LCA，输出结果

        观察倍增算法在树上的实现，我们发现其实跟兔子跳格子是一样的，从每个节点跳几步会到哪个节点是需要我们预处理出来的，方法就跟聪明小白兔晚上打小抄的方法一致，在真正跳的时候，也跟聪明小白兔的方式一致。

        也许，现在你更加明白倍增算法最后的那段话了，从一个节点，若想往上跳2步，在没有预处理的情况下你只能1步1步的跳，因为你只能知道当前节点的父节点是谁，而无法知道爷爷节点是谁。

【尾声】

        LCA其实是个特别好玩的东西，很多在树结构中难以想到的东西都或多或少可以用到LCA的思想来工作，更多神秘的东西就等待你去发现啦。

                                                                                                                                               完