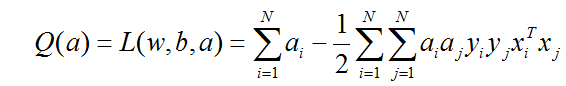matlab体验svm算法【非实现】

SVM算法实现工具有很多，包括svm light，libsvm，有matlab本身自带的svm工具包等。

网友们一般都研究Microsoft Research的John C.Platt的SMO算法

大家可以参照：

http://blog.csdn.net/techq/article/details/6171688，这是网友用java实现了smo算法，说预测准确率73%

http://download.csdn.net/detail/jinshengtao/6786461，这是我上传的libsvm2.5程序代码注释解读，内附实现

本文的目的，是用matlab体验一下如何求解条件极值实现svm对线性数据进行分类。

上一篇文章说，如何求解SVM的权值和偏置，最后通过以下方程的最大值实现：

我们可以使用matlab自带的fmincon函数，求-Q(a)的最小值来得到分界线。

输入数据为100个样本点【其实就是100个坐标点】，由于是二分类问题，网络结构就一个神经元

	clear all;
	close all;
	
	%%%%%%%%%%%%%%%%%%数据%%%%%%%%%%%%%%%%%%%%%
	x1(1,1)=5.1418; x1(1,2)=0.5950;
	x1(2,1)=5.5519; x1(2,2)=3.5091;
	x1(3,1)=5.3836; x1(3,2)=2.8033;
	x1(4,1)=3.2419; x1(4,2)=3.7278;
	x1(5,1)=4.4427; x1(5,2)=3.8981;
	x1(6,1)=4.9111; x1(6,2)=2.8710;
	x1(7,1)=2.9259; x1(7,2)=3.4879;
	x1(8,1)=4.2018; x1(8,2)=2.4973;
	x1(9,1)=4.7629; x1(9,2)=2.5163;
	x1(10,1)=2.7118; x1(10,2)=2.4264;
	x1(11,1)=3.0470; x1(11,2)=1.5699;
	x1(12,1)=4.7782; x1(12,2)=3.3504;
	x1(13,1)=3.9937; x1(13,2)=4.8529;
	x1(14,1)=4.5245; x1(14,2)=2.1322;
	x1(15,1)=5.3643; x1(15,2)=2.2477;
	x1(16,1)=4.4820; x1(16,2)=4.0843;
	x1(17,1)=3.2129; x1(17,2)=3.0592;
	x1(18,1)=4.7520; x1(18,2)=5.3119;
	x1(19,1)=3.8331; x1(19,2)=0.4484;
	x1(20,1)=3.1838; x1(20,2)=1.4494;
	x1(21,1)=6.0941; x1(21,2)=1.8544;
	x1(22,1)=4.0802; x1(22,2)=6.2646;
	x1(23,1)=3.0627; x1(23,2)=3.6474;
	x1(24,1)=4.6357; x1(24,2)=2.3344;
	x1(25,1)=5.6820; x1(25,2)=3.0450;
	x1(26,1)=4.5936; x1(26,2)=2.5265;
	x1(27,1)=4.7902; x1(27,2)=4.4668;
	x1(28,1)=4.1053; x1(28,2)=3.0274;
	x1(29,1)=3.8414; x1(29,2)=4.2269;
	x1(30,1)=4.8709; x1(30,2)=4.0535;
	x1(31,1)=3.8052; x1(31,2)=2.6531;
	x1(32,1)=4.0755; x1(32,2)=2.8295;
	x1(33,1)=3.4734; x1(33,2)=3.1919;
	x1(34,1)=3.3145; x1(34,2)=1.8009;
	x1(35,1)=3.7316; x1(35,2)=2.6421;
	x1(36,1)=2.8117; x1(36,2)=2.8658;
	x1(37,1)=4.2486; x1(37,2)=1.4651;
	x1(38,1)=4.1025; x1(38,2)=4.4063;
	x1(39,1)=3.9590; x1(39,2)=1.3024;
	x1(40,1)=1.7524; x1(40,2)=1.9339;
	x1(41,1)=3.4892; x1(41,2)=1.2457;
	x1(42,1)=4.2492; x1(42,2)=4.5982;
	x1(43,1)=4.3692; x1(43,2)=1.9794;
	x1(44,1)=4.1792; x1(44,2)=0.4113;
	x1(45,1)=3.9627; x1(45,2)=4.2198;

	x2(1,1)=9.7302; x2(1,2)=5.5080;
	x2(2,1)=8.8067; x2(2,2)=5.1319;
	x2(3,1)=8.1664; x2(3,2)=5.2801;
	x2(4,1)=6.9686; x2(4,2)=4.0172;
	x2(5,1)=7.0973; x2(5,2)=4.0559;
	x2(6,1)=9.4755; x2(6,2)=4.9869;
	x2(7,1)=9.3809; x2(7,2)=5.3543;
	x2(8,1)=7.2704; x2(8,2)=4.1053;
	x2(9,1)=8.9674; x2(9,2)=5.8121;
	x2(10,1)=8.2606; x2(10,2)=5.1095;
	x2(11,1)=7.5518; x2(11,2)=7.7316;
	x2(12,1)=7.0016; x2(12,2)=5.4111;
	x2(13,1)=8.3442; x2(13,2)=3.6931;
	x2(14,1)=5.8173; x2(14,2)=5.3838;
	x2(15,1)=6.1123; x2(15,2)=5.4995;
	x2(16,1)=10.4188; x2(16,2)=4.4892;
	x2(17,1)=7.9136; x2(17,2)=5.2349;
	x2(18,1)=11.1547; x2(18,2)=4.4022;
	x2(19,1)=7.7080; x2(19,2)=5.0208;
	x2(20,1)=8.2079; x2(20,2)=5.4194;
	x2(21,1)=9.1078; x2(21,2)=6.1911;
	x2(22,1)=7.7857; x2(22,2)=5.7712;
	x2(23,1)=7.3740; x2(23,2)=2.3558;
	x2(24,1)=9.7184; x2(24,2)=5.2854;
	x2(25,1)=6.9559; x2(25,2)=5.8261;
	x2(26,1)=8.9691; x2(26,2)=4.9919;
	x2(27,1)=7.3872; x2(27,2)=5.8584;
	x2(28,1)=8.8922; x2(28,2)=5.7748;
	x2(29,1)=9.0175; x2(29,2)=6.3059;
	x2(30,1)=7.0041; x2(30,2)=6.2315;
	x2(31,1)=8.6396; x2(31,2)=5.9586;
	x2(32,1)=9.2394; x2(32,2)=3.3455;
	x2(33,1)=6.7376; x2(33,2)=4.0096;
	x2(34,1)=8.4345; x2(34,2)=5.6852;
	x2(35,1)=7.9559; x2(35,2)=4.0251;
	x2(36,1)=6.5268; x2(36,2)=4.3933;
	x2(37,1)=7.6699; x2(37,2)=5.6868;
	x2(38,1)=7.8075; x2(38,2)=5.0200;
	x2(39,1)=6.6997; x2(39,2)=6.0638;
	x2(40,1)=5.6549; x2(40,2)=3.6590;
	x2(41,1)=6.9086; x2(41,2)=5.4795;
	x2(42,1)=7.9933; x2(42,2)=3.3660;
	x2(43,1)=5.9318; x2(43,2)=3.5573;
	x2(44,1)=9.5157; x2(44,2)=5.2938;
	x2(45,1)=7.2795; x2(45,2)=4.8596;
	x2(46,1)=5.5233; x2(46,2)=3.8697;
	x2(47,1)=8.1331; x2(47,2)=4.7075;
	x2(48,1)=9.7851; x2(48,2)=4.4175;
	x2(49,1)=8.0636; x2(49,2)=4.1037;
	x2(50,1)=8.1944; x2(50,2)=5.2486;
	x2(51,1)=7.9677; x2(51,2)=3.5103;
	x2(52,1)=8.2083; x2(52,2)=5.3135;
	x2(53,1)=9.0586; x2(53,2)=2.9749;
	x2(54,1)=8.2188; x2(54,2)=5.5290;
	x2(55,1)=8.9064; x2(55,2)=5.3435;
    for i=1:45 r1(i)=x1(i,1);end;
	for i=1:45 r2(i)=x1(i,2);end;
	for i=1:55 r3(i)=x2(i,1);end;
	for i=1:55 r4(i)=x2(i,2);end;
	
	figure(1);
	plot(r1,r2,'*',r3,r4,'o');
	axis([0,12,0,8]);
    
    for i=1:45 x(i,1)=x1(i,1);x(i,2)=x1(i,2);
	y(i,1)=1;end;
	for i=1:55 x(i+45,1)=x2(i,1);x(i+45,2)=x2(i,2);
	y(i+45,1)=-1;end;
	X=[x];                    %样本向量
	Y=[y];
	
	lambda0=zeros(100,1);        %初始值
	A=[];b=[];                  %无线性不等式约束
	Aeq=Y';beq=0;              %线性等式约束
	lb=zeros(100,1);             %上下界约束
	[lambda,fval]=fmincon(@fun,lambda0,A,b,Aeq,beq,lb);        
	w = X'*(lambda.*Y)           %支撑矢量
	
	epsilon = 1e-5;                 %计算w0
	index = find(lambda > epsilon); 
	sum=0;
	for i=1:length(index)
	    j=index(i);
	    sum=sum+1/y(j) - X(j,:)*w;
	end
	w0 =  (1/length(index))*sum;
	
	%作出分类线
	h=gca;
	XLim=get(h,'Xlim');
	YLim=-XLim*w(1)/w(2)-w0/w(2);
	h=line([XLim(1),XLim(2)],[YLim(1),YLim(2)]);
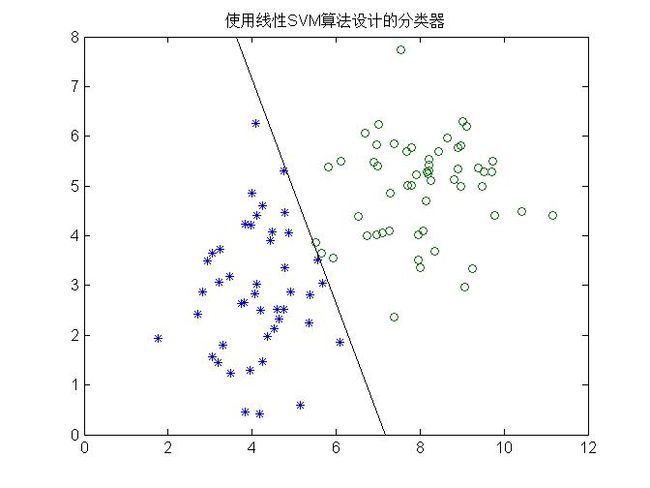
	title('使用线性SVM算法设计的分类器');
	set(h,'color','k')

      function f_lambda = fun(lambda)
                    f_lambda=(-1*ones(100,1))'*lambda+1/2*(lambda.*y)'*X*X'*(lambda.*y);

具体结果：

代码中flambda表达式就是我们的 -Q(a)。如果要进行预测的话，输入第101个坐标，根据现在求得的分界面，可以判断他属于哪半面。

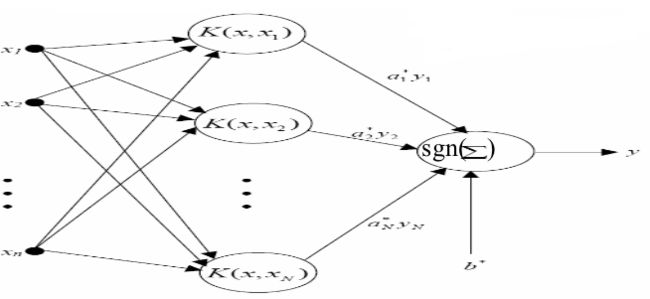
对于非线性问题的二分类，可以在用上述公式之前，先用核函数K处理一下，比如：