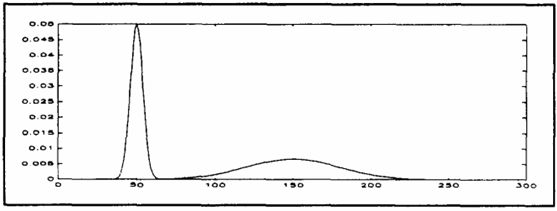
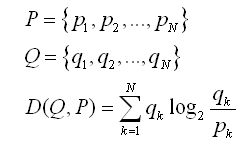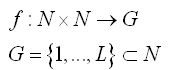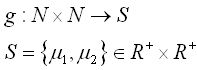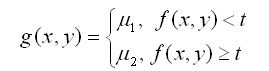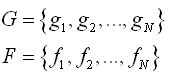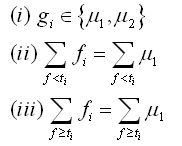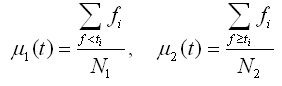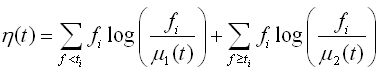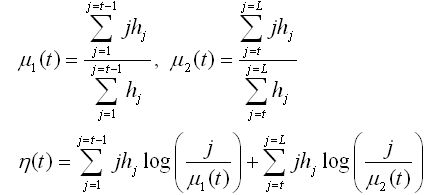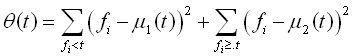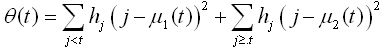最小交叉熵图像分割(Minimum cross entropy thresholding)
本文是Li和Lee关于一维最小交叉熵图像阈值分割的原文。这里进行了简单翻译,有不足的地方请大家一起讨论完善。后续有文章对信息熵学进行初窥,敬请期待。
摘要:通过最小化图像与其部分区域之间的交叉熵解决了图像分割中的阈值选取问题。其中交叉熵基于两幅图像之间的像素运算得到,同时提出一种基于统计直方图的实现算法。该方法提出了一种信息理论意义上针对二值图像的无偏估计,因而不需要了解图像灰度分布的先验知识。
1、介绍
在众多的模式识别系统中,图像阈值化是重要的一个初步环节。其中阈值的选取会影响到后期图像分割的精度以及效率。本文的方法假设图像中的背景和待分割目标可以通过将图像的灰度值与选定的一个合适的阈值对比而区分。分割图像可能不适合作为通常意义上的图像处理例程的输入,因为在空间范围内它缺少对图像像素的更多有效信息。尽管如此,这种阈值化算法实现简单并且运行速度高,这使得它成为目前包括从医学英语到工业制造的众多自动化系统中使用最广泛的算法。二值化图像同样很适合在硬件上通过相关性以及实时识别进行模板匹配处理。除了在图像分割中全局阈值化的应用外,这种方法同样可以用于模式识别领域的众多分类问题中。
关于阈值选取研究工作的详细总数可以在参考文献1-3中找到。通常来说,阈值选取算法可以根据算法的性质粗略划分为全局方法和局部方法。局部阈值化算法基于直方图函数的局部属性来选取阈值,比如根据存在的极大值和极小值。一个典型局部阈值化算法的例子是基于直方图局部最小值定位的谷底(thebottom of the valley approach)算法。从原理上讲,这种方法依赖于灰度差值因此对噪声比较敏感。因而在这个过程中很重要的预处理就是对图像及其直方图进行平滑。此外,往往当地的极值点不一定保证存在,这时可采用直方图增强或者锐化算法用来克服解决这些困难。局部阈值化算法的一个优点就是它不需要先验知识就可以确定类别的数量。全局阈值化算法则是通过对直方图进行全局统计而得到选取标准。这种方法降低了对噪声的敏感度并且不需要进行图像增强,这些增强通常对单个的图像特征很敏感并且需要监督。最近以来,Wilson和Spann介绍了一种将局部阈值化方法和全局阈值化方法结合起来的集群算法,这种算法消除了以上大多数的不足之处。在本文中,作者仅讨论全局阈值化方法,同时采用目前使用最广的两种算法进行了对比:Kittler与Illingworth提出的最小误差阈值算法以及Ostu算法。在大津算法中,阈值的选取是通过最大化类间方差实现的,这种方法基于类内的方差,类间方差以及整个灰度级的全局方差。该方法不需要输入参数,无需监督并且无需先验知识。该方法目前应用广泛,并且通常被当做标准算法与其他阈值算法结果进行比较。其主要不足是当两个基本分布存在不同方差时或者两个分布所包含元素数有较大不同时,该方法在阈值估计上存在偏差。
在最小误差算法中,包括目标和背景的像素集都假定为正态分布。阈值选取的准则是使得像素集之间的平均误差最小。除了假设正态分布外,该方法还假设两个总体分布重叠较小同时推倒中所产生的截断误差可忽略。该方法试图绕过对直方图中两个分布均值,方差以及标准差的估计。当灰度确实是正态分布时该方法可以对阈值给出较好的估计,而当分布为单峰的正态分布时,该方法不能给出阈值估计。Cho等人对最小误差算法提出了改进,他们对截断造成的方差估计偏差进行了修正。由于建模的原理都是一致的,我们将参考文献5作为基础进行讨论和比较。
以上两个算法是将统计直方图作为唯一输入的的阈值化算法的代表。另外一类的阈值化算法同样仅仅使用到了统计直方图,这些方法应用到了包括图像分割问题的最大熵值原理。这些方法用到了信息理论中熵的概念,其不用明确参考图像属性,比如二维分布以及在实际应用中有显著的限制。算法细节将在第3部分讨论。
2、最大熵原理
最大熵原理最早由Jaynes提出来,用于估计限制条件下的未知概率分布。这些限制的作用是将解决方案集限制在只包括与数据相一致的解决方案范围内。推理问题常常因为数据不足而变得不确定,因此在应用了所有的限制条件后,往往还有多种解决方案存在。最大熵值原理允许我们选择给出最大熵值(信息)的方案。最初的想法是它将会给出无偏的估计,并且在限制范围内允许最大的自由度。这些年来,最大熵理论经历了广泛的理论辩论并且已经成功的应用到了科学与工程的多个领域。浓度定理(ConcentrationTheorem)和多重性的研究表明,更高的熵值具有更好的多重性,因而更易被观测到。显而易见的,在新信息以期望值给定的时候最大熵值方法是归纳推理的唯一正确方法。它被延伸到一般的推理方法,用于处理包括非相干图像强度或者功率谱密度的分布等领域。总的来说,该方法已经被广泛应用于各种领域并且证明是成功的。例如,在谱估计领域,最大熵可以提供比传统估计方法如极大似然法更高的分辨率。
Kullback提出交叉熵的时候命名为定向差异(directed divergence)。交叉熵测量两个分布P和Q之间的信息理论距离,其中定义如下:公式(1)
Renyi等人同样对D的测量进行了研究,他们将D看做这两个分布之间的信息理论距离。Renyi还指出当我们用Q取代P时,此公式可解释为信息内容变化的期望。最小交叉熵方法可以看做是最大熵法的扩展,条件是为上公示中所有的p设置相等的初始估计,并且没有先验信息存在。
3、最小交叉熵分割法
对于投掷筛子这样一个实验来说,每次投掷是一个单独的事件,不会影响其他投掷的结果,熵最大化会导致不同投掷的独立结果概率。尽管如此,对于时间序列分析或者图像建模来说,数据间有较强的联系,为了考虑相互之间的信息内容,模型必须将时间序列或者图像作为一个单一的抽样,同时将最大熵原理的组合参数应用到许多不同抽样试验中。
将最大熵方法用于图像分割,之前的研究工作没有考虑上述的区别并且将像素产生的过程看做是独立试验。他们基于具有一定灰度级单个像素的随机试验和测量像素分布的熵,将归一化的灰度直方图作为灰度级的概率分布。Kapur提出的最大熵阈值化方法被认为由于其他的熵谱阈值算法。尽管如此,最大熵方法仍然没有被很好接受,并且性能较差,因而有大量工作对其进行了改进。Wong和Sahoo结合图像中的空间信息和熵来产生阈值选取标准。在最大熵值方法中保留了直方图熵函数的同时,Kapur介绍了一系列附加的启发式原则来选择阈值。综上可知,不采用附加准则而仅仅通过熵原理制定通用的直方图阈值算法是不成功。
在计划中,分割过程是一个图像分布重建的过程。考虑图像函数如下:其中N是正整数,G为灰度集合。分割过程就是重建如下函数:
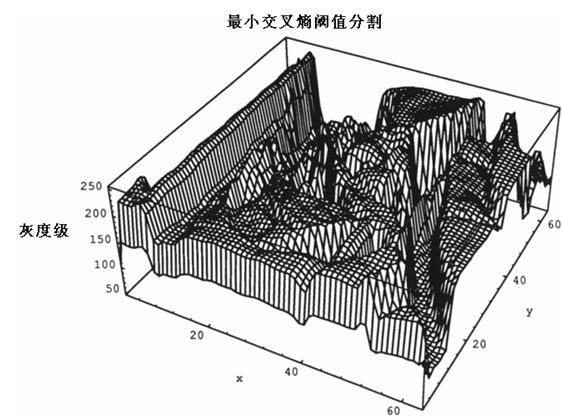
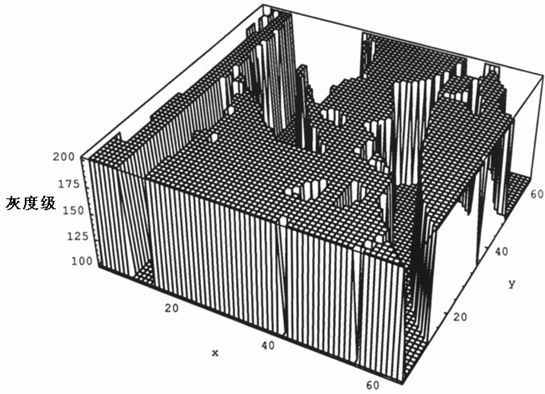
其中的R+是正的实整数。图1和图2展现了一个源图像f(x,y)和一个分割图像g(x,y),其中坐标系的z轴代表了图像的灰度级。分割图像g(x,y)将按照下式进行重构:
公式(2)
图1 灰度图像的三维图(Z为灰度级)
图2 分割图像的三维图
此分割图像g(x,y)来自f(x,y),具体形式由三个未知的参数决定。必须建立准则来寻找最有的g,或者等价的三个参数,使其尽可能的与f相似。可表达如下:
公式(3)
准则函数一般是某种失真测量,例如从f到g的均方根差时常用的措施。最小误差法和大津法都属于这种方法。在这一章的结尾,我们将会展示大津法最小化图像和分割区域之间的最小均方差,而我们提出的是最小化交叉熵方法。交叉熵法没有采用均方差,这种方法注重对正像分布的测量。
上面提出的问题可以作为一个带限制条件的经典的最大熵推理问题。对问题重述如下:G为一系列的值,N是图像中的像素点个数,F为源图像,现在要根据F和可用的限制条件来求得G向量。这里用相同的方式通过线性化2维分布得到新的分布,因此G和F中的元素来自图像空间同样的像素位置,同时G包括了只有两个值的元素,该元素目前还未知。接下来,将要用到强度保护约束。由于我们想要重建图像的分布,观测图像强度F会给G中的两个元素带来约束,这样使得重建图像中总的强度与观测图像相等。限制表达式如下:
公式(4)
这样,该两个参数可以由如下公式来确定:
公式(5)
其中N1和N2分别为两个区域内的像素点个数。联合以上公式1、2和5可以得到:
公式(6)
阈值可以选取为:
其中t0即为所需要的门限值。以上的和在整幅图像上进行,尽管如此,有一些可替换的计算可分类。这样就得到了如下的公式:
公式(8)
以上模型中的交叉熵的形式看起来和Skilling推倒的图像分割方法很相似,在他的方法中用到了4个公理推出如下的熵函数:
公式(9)
其中 f(x)是图像强度分布函数,m(x)是图像模型。实际上,如果包括总的强度转换限制,这两个方程只差一个符号,因为8公式中的两个积分在整个类上积分将会抵消。
以上的方法介绍了最小化图像和分割区域之间的交叉熵。大津法最小化类间方差也可以从以上的方法中推导出来,这要用到两幅图像之间的均方差并且如4式所示的同样的限制。这样标准函数就变为如下形式:公式(10)
用直方图进行分类,标准函数就如下所示:
公式(11)
类内方差6式进行了定义,最小化11式所定义的函数等效于最大化大津法的准则,因为类内方差以及类间方差的和与选择的阈值相独立。
交叉熵函数的使用不仅仅限于阈值图像分割。结合其他的限制,可以将该算法扩展到图像分割的其他领域。例如,有些基于区域的分割方法就用交叉熵作为准则,比如分裂与合并方法,合并的地区可根据空间坐标标签的限制来确定。
4、算法的应用和讨论
为了进行对比,这里采用Kittler和Illingworth提出的算法,大津算法,最小误差方法以及最小交叉熵算法被用于参考文献5所讨论的正态分布。这些直方图如图3-5所示。我们同样采用了真实工业图像的直方图。根据这些方法所选择的阈值在表1中展示。图3 直方图a
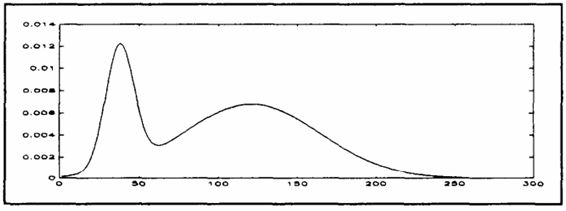
图4 直方图b
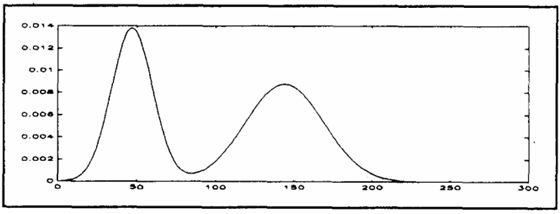
图5 直方图c
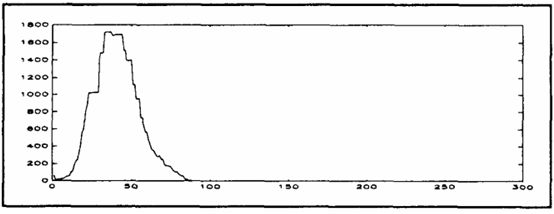
图6 直方图d
前三个直方图的对高斯分布结果可以总结为:最小误差方法将正态分布作为模型,随后优于最小交叉熵和大津算法。尽管如此,最小交叉熵能够给出一个优化的阈值,这个数值相比大津算法和最大熵算法更加接近于最有的阈值。
对于图7所示的劳损测量图像,我们的目标是测量椭圆形的主轴和次轴的变化,这些将会给出金属的应变信息。第一步是进行平行线和椭圆从背景中的分割。直方图被提取出来如图6所示。最小误差法没有给出任何阈值信息,因为针对该标准函数没有内部最小值存在。直方图将其错误的推断为单峰,而实际情况是这两个分布因为有大量噪声而高度重叠。这表明错误的假设可能是灾难性的。最小交叉熵方法和大津法能成功的选取阈值,相比其他方法该阈值能够使得分割图像有较低的噪声水平。
为了进行证明,对比图8和图9、图10,图8显示了最小交叉熵法的分割图像(选定的阈值为40),图9和图10分别显示了小于40与大于40时的分割图像。图9中出现了更多的洞,还有开裂的线条以及椭圆。图示包括了太多的背景。这说明了选择正确的阈值是很关键的,因为他将产生高度重叠的分布。
关于最后测试的图,详见作者原文。可从我的资源里面下载, 点击这里 。