(九)分支限界法
分支限界法(branch and bound method)按广度优先策略搜索问题的解空间树,在搜索过程中,对待处理的节点根据限界函数估算目标函数的可能取值,从中选取使目标函数取得极值(极大或极小)的结点优先进行广度优先搜索,从而不断调整搜索方向,尽快找到问题的解。分支限界法适合求解最优化问题。
1、分支限界法思想
上节中回溯法是从根节点出发,按照深度优先的策略搜索问题的解空间树,在搜索过程中,如果某点所代表的部分解不满足约束条件,则对该节点为根的子树进行剪枝;否则继续按照深度优先的策略搜索以该结点为根,当搜索到一个满足的约束条件的叶子结点时,就找到了一个可行解。
分支限界法首先要确定一个合理的限界函数(bound funciton),并根据限界函数确定目标函数的界[down ,up],按照广度优先策略搜索问题的解空间树,在分直结点上依次扩展该结点的孩子结点,分别估算孩子结点的目标函数可能值,如果某孩子结点的目标函数可能超出目标函数的界,则将其丢弃;否则将其加入待处理结点表(简称PT表),依次从表PT中选取使目标函数取得极值的结点成为当前扩展结点,重复上述过程,直到得到最优解。
2、TSP问题中使用分支限界法
【TSP问题】:
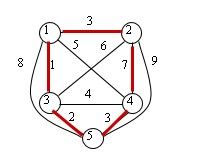
TSP问题是指旅行家要旅行n个城市,要求各个城市经理且仅经理依次然后回到出发城市,并要求所走的路程最短。我们以下图的无限图为例,采用分支限界法解决这个问题。
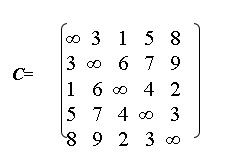
该无向图对应的代价矩阵如下所示:
代价矩阵是1到1,1到2,1到3,1到4,1到5距离写在第一行,第二行为2到1,2到2,2到3,2到4,、、、依次
(1)找到目标函数的界。上界为,采用贪心算法求得上界,从节点1开始到节点3--->5--->4--->2--->1,路径,即为图中红色圈的路径,其路径长度为C=1+2+3+7+3=16。
下界为矩阵中每行中两个最小的相加,所有的行加起来的和的一半。( (3+1)+(3+6)+(1+2)+(3+4)+(2 +3) )/2=14
所以求得界为[14,16]。
(2)计算每个节点的限界值。
计算目标函数(限界函数),lb分为三部分,第一部分是经过路径的长度相加的2倍,加上第二部分离着路径首尾节点最近的距离相加(不在已知路径上的),加上第三部分除了路径上节点,矩阵中两个最短的距离相加,最后这三部分和相加,得到的结果除以2便是每个节点的限界值。
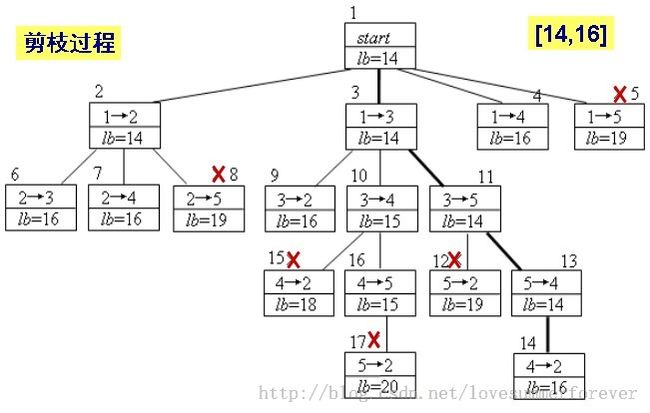
(3)画出PT图。如下所示。
根据上述所述得到最优解1-->3-->5-->4-->2-->1
【C代码】:
//分支限界法
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<queue>
#define INF 100000
using namespace std;
/* n*n的一个矩阵 */
int n;
int mp[22][22];//最少3个点,最多15个点
/*输入距离矩阵*/
void in()
{
scanf("%d",&n);
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
if(i==j)
{
mp[i][j]=INF;
continue;
}
scanf("%d",&mp[i][j]);
}
}
}
struct node
{
int visp[22];//标记哪些点走了
int st;//起点
int st_p;//起点的邻接点
int ed;//终点
int ed_p;//终点的邻接点
int k;//走过的点数
int sumv;//经过路径的距离
int lb;//目标函数的值
bool operator <(const node &p )const
{
return lb>p.lb;
}
};
priority_queue<node> q;
int low,up;
int inq[22];
//确定上界
int dfs(int u,int k,int l)
{
if(k==n) return l+mp[u][1];
int minlen=INF , p;
for(int i=1; i<=n; i++)
{
if(inq[i]==0&&minlen>mp[u][i])/*取与所有点的连边中最小的边*/
{
minlen=mp[u][i];
p=i;
}
}
inq[p]=1;
return dfs(p,k+1,l+minlen);
}
int get_lb(node p)
{
int ret=p.sumv*2;//路径上的点的距离
int min1=INF,min2=INF;//起点和终点连出来的边
for(int i=1; i<=n; i++)
{
if(p.visp[i]==0&&min1>mp[i][p.st])
{
min1=mp[i][p.st];
}
}
ret+=min1;
for(int i=1; i<=n; i++)
{
if(p.visp[i]==0&&min2>mp[p.ed][i])
{
min2=mp[p.ed][i];
}
}
ret+=min2;
for(int i=1; i<=n; i++)
{
if(p.visp[i]==0)
{
min1=min2=INF;
for(int j=1; j<=n; j++)
{
if(min1>mp[i][j])
min1=mp[i][j];
}
for(int j=1; j<=n; j++)
{
if(min2>mp[j][i])
min2=mp[j][i];
}
ret+=min1+min2;
}
}
return ret%2==0?(ret/2):(ret/2+1);
}
void get_up()
{
inq[1]=1;
up=dfs(1,1,0);
}
void get_low()
{
low=0;
for(int i=1; i<=n; i++)
{
/*通过排序求两个最小值*/
int min1=INF,min2=INF;
int tmpA[22];
for(int j=1; j<=n; j++)
{
tmpA[j]=mp[i][j];
}
sort(tmpA+1,tmpA+1+n);//对临时的数组进行排序
low+=tmpA[1];
}
}
int solve()
{
/*贪心法确定上界*/
get_up();
/*取每行最小的边之和作为下界*/
get_low();
/*设置初始点,默认从1开始 */
node star;
star.st=1;
star.ed=1;
star.k=1;
for(int i=1; i<=n; i++) star.visp[i]=0;
star.visp[1]=1;
star.sumv=0;
star.lb=low;
/*ret为问题的解*/
int ret=INF;
q.push(star);
while(!q.empty())
{
node tmp=q.top();
q.pop();
if(tmp.k==n-1)
{
/*找最后一个没有走的点*/
int p;
for(int i=1; i<=n; i++)
{
if(tmp.visp[i]==0)
{
p=i;
break;
}
}
int ans=tmp.sumv+mp[p][tmp.st]+mp[tmp.ed][p];
node judge = q.top();
/*如果当前的路径和比所有的目标函数值都小则跳出*/
if(ans <= judge.lb)
{
ret=min(ans,ret);
break;
}
/*否则继续求其他可能的路径和,并更新上界*/
else
{
up = min(up,ans);
ret=min(ret,ans);
continue;
}
}
/*当前点可以向下扩展的点入优先级队列*/
node next;
for(int i=1; i<=n; i++)
{
if(tmp.visp[i]==0)
{
next.st=tmp.st;
/*更新路径和*/
next.sumv=tmp.sumv+mp[tmp.ed][i];
/*更新最后一个点*/
next.ed=i;
/*更新顶点数*/
next.k=tmp.k+1;
/*更新经过的顶点*/
for(int j=1; j<=n; j++) next.visp[j]=tmp.visp[j];
next.visp[i]=1;
/*求目标函数*/
next.lb=get_lb(next);
/*如果大于上界就不加入队列*/
if(next.lb>up) continue;
q.push(next);
}
}
}
return ret;
}
int main()
{
in();
printf("%d\n",solve());
return 0;
}
3、分支限界法解决0/1背包问题。
在这里只写个思路,相对来说也是比较简单的。
(1)首先将背包按照价值由大到小进行排列。
(2)找到上界和下界,背包问题的下界把第一个价值最大的装入背包。上界,采用背包问题的贪心算法(三种策略)最终求得上界。
(3)限界函数ub=v+(W-w)*(v i+1 / w i+1)
(4)画PT表格,每个节点进行判断是否剪枝。最终得到最优解。
算法设计与分析大概总结到这。
学习是一点一点深入的,这一点体会是多么的深刻,就像我的牙齿一样,黑的部分不是一天两天能黑的,牙疼的引起也不是一天两天的事情,要有牙齿病菌的这种精神!~~~