【算法导论】图的深度优先搜索遍历（DFS）

        关于图的存储在上一篇文章中已经讲述，在这里不在赘述。下面我们介绍图的深度优先搜索遍历（DFS）。

        深度优先搜索遍历实在访问了顶点vi后，访问vi的一个邻接点vj；访问vj之后，又访问vj的一个邻接点，依次类推，尽可能向纵深方向搜索，所以称为深度优先搜索遍历。显然这种搜索方法具有递归的性质。图的BFS和树的搜索遍历很类似，只是其存储方式不同。

        其基本思想为：从图中某一顶点vi出发，访问此顶点，并进行标记，然后依次搜索vi的每个邻接点vj；若vj未被访问过，则对vj进行访问和标记，然后依次搜索vj的每个邻接点; 若vj的邻接点未被访问过，则访问vj的邻接点，并进行标记，直到图中和vi有路径相通的顶点都被访问。若图中尚有顶点未被访问过（非连通的情况下），则另选图中的一个未被访问的顶点作为出发点，重复上述过程，直到图中所有顶点都被访问为止。

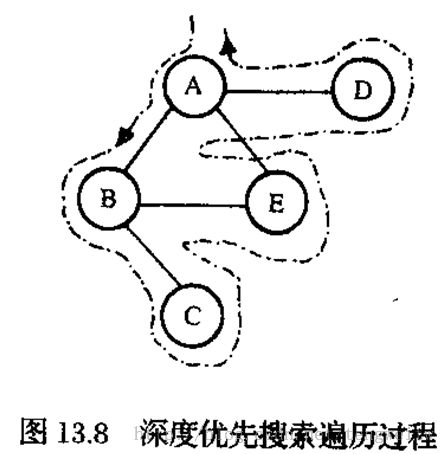
在下面的程序中，假设图如下所示：

A B C D E对应的序号分别为0 1 2 3 4.上图的轨迹为一种深度优先搜索遍历。

具体的程序实现如下：

#include<stdio.h>
#include<stdlib.h>
#define N 5

typedef struct 
{
	char vexs[N];//顶点数组
	int arcs[N][N];//邻接矩阵
}graph;

//图的两种存储方法的结构体
typedef struct Node
{
	int adjvex;
	struct Node *next;
}edgenode;

typedef struct
{
	char vertex;
	edgenode *link;
}vexnode;

//队列的结构体
typedef struct node
{
	int data;
	struct node *next;
}linklist;

typedef struct
{
	linklist *front,*rear;
}linkqueue;

void DFS_matrix(graph g,int i,int visited[N]);//图按照邻接矩阵存储时的深度优先搜索遍历
void DFS_AdjTable(vexnode ga[N],int i,int visited[N]);//图按照邻接矩表存储时的深度优先搜索遍历


void SetNull(linkqueue *q)//置空
{
	q->front=(linklist *)malloc(sizeof(linklist));
	q->front->next=NULL;
	q->rear=q->front;
}

int Empty(linkqueue *q)//判空
{
	if(q->front==q->rear)
		return 1;
	else 
		return 0;
}

int Front(linkqueue *q)//取队头元素
{
	if(Empty(q))
	{
		printf("queue is empty!");
		return -1;
	}
	else
		return q->front->next->data;
}

void ENqueue(linkqueue *q,int x)//入队
{
	linklist * newnode=(linklist *)malloc(sizeof(linklist));
    q->rear->next=newnode;
	q->rear=newnode;
	q->rear->data=x;
	q->rear->next=NULL;
	
}

int DEqueue(linkqueue *q)//出队
{
	int temp;
	linklist *s;
	if(Empty(q))
	{
		printf("queue is empty!");
		return -1;
	}
	else
	{
		s=q->front->next;
		if(s->next==NULL)
		{
			q->front->next=NULL;
			q->rear=q->front;
		}
		else
			q->front->next=s->next;
		temp=s->data;
		return temp;
	}
}



void CreateAdjTable(vexnode ga[N],int e)//创建邻接表
{
	int i,j,k;
	edgenode *s;
	printf("\n输入顶点的内容：");
	for(i=0;i<N;i++)
	{
		//scanf("\n%c",ga[i].vertex);
		
		ga[i].vertex=getchar();
		
		ga[i].link=NULL;//初始化
	}
	printf("\n");
	for(k=0;k<e;k++)
	{
		printf("输入边的两个顶点的序号:");
		scanf("%d%d",&i,&j);//读入边的两个顶点的序号
		s=(edgenode *)malloc(sizeof(edgenode));
		s->adjvex=j;
		s->next=ga[i].link;
		ga[i].link=s;

		s=(edgenode *)malloc(sizeof(edgenode));
		s->adjvex=i;
		s->next=ga[j].link;
		ga[j].link=s;

	}
}


void main()
{
	graph g;
	int visited[5]={0};//初始化
	int visited1[5]={0};
	g.vexs[0]='A';
	g.vexs[1]='B';
	g.vexs[2]='C';
	g.vexs[3]='D';
	g.vexs[4]='E';
	int a[5][5]={{0,1,0,1,1},{ 1,0,1,0,1},{ 0,1,0,0,0},{ 1,0,0,0,0},{ 1,1,0,0,0}};
	for(int i=0;i<5;i++)
		for(int j=0;j<5;j++)
			g.arcs[i][j]=a[i][j];
	printf("图按照邻接矩阵存储时的深度优先搜索遍历：\n");
	DFS_matrix(g,0,visited);
	vexnode ga[N];
	CreateAdjTable(ga,5);//5为边的条数
		printf("图按照邻接表存储时的深度优先搜索遍历：\n");
    DFS_AdjTable(ga,0,visited1);//0为开始的顶点的序号


}

void DFS_matrix(graph g,int i,int visited[N])
{
	printf("%c\n",g.vexs[i]);
	visited[i]=1;
	for(int j=0;j<N;j++)
		if(g.arcs[i][j]==1&&visited[j]==0)//是否有未被访问的邻接点
			DFS_matrix(g,j,visited);//递归
}

void DFS_AdjTable(vexnode ga[N],int i,int visited[N])
{
	edgenode *p;
	printf("%c\n",ga[i].vertex);
	visited[i]=1;
	p=ga[i].link;
	while(p!=NULL)//p是否为空
	{
		if(visited[p->adjvex]==0)
			DFS_AdjTable(ga,p->adjvex,visited);
		p=p->next;
	}
}

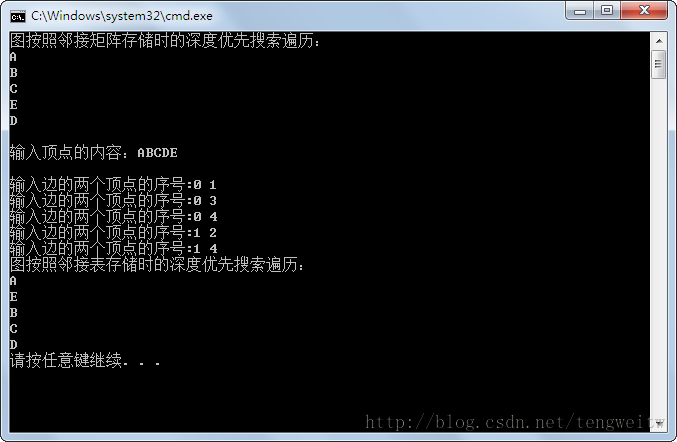
其结果如下：

从上面可以看出，两种方式的结果不同，但都是正确的，因为这与邻接点访问的顺序有关。

注：如果程序出错，可能是使用的开发平台版本不同，请点击如下链接： 解释说明

原文：http://blog.csdn.net/tengweitw/article/details/17248643

作者：nineheadedbird