【线性代数】线性相关性、基和维数
一、线性相关性

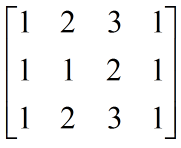
什么情况下,向量X1,X2,……,Xn是线性无关的?
答:当向量X1,X2,……,Xn的线性组合(线性组合时系数不能全为0)不为零向量时,它们是线性无关的。即方程
不存在非零解。
对于一个矩阵A来说,当A总各列向量是线性无关时,则Ax=0的解只有0向量,即矩阵A的零空间只有零向量。 如果各列向量是相关的,则矩阵A的零空间中还存在一些其他的向量。
当矩阵A各列是线性无关的,则矩阵A各列都有主元,自由变量的个数为0。
二、空间的基
我们知道,矩阵各列的线性组合生成矩阵的列向量。但是,矩阵的各列有可能不是线性相关的。我们关心的是这样的一组向量:既能生成空间,又是线性无关的。这样的向量我们称为空间的基。
如果要确定一个空间,我们只需要知道该空间的基,就了解了该空间的所有信息。例如:在三维空间中,向量的一个基是:

当然,我们还可以写出其他的基,只需要满足基的两个性质:1、生成空间;2、线性无关。但是基中向量的个数是一样的。
对于一个n阶的方阵A的各列想要成为n维空间的基的话,该方阵必须是可逆的。
三、空间的维数
维数的定义:空间内任意基内向量个数称为空间的维数。
空间内所有的基内向量个数是相同的,都指空间的维数。
下面我们来举例说明上述概念:假设矩阵为A:
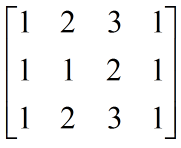
矩阵A的各列生成矩阵A的列空间。
矩阵A的各列不是A的列空间的基,因为它们线性相关,列空间的一个基是矩阵的第一、二列。
我们可以通过消元知道,该矩阵的秩为2,该列空间的维数为2。即矩阵的秩是列空间的维数!
原文:http://blog.csdn.net/tengweitw/article/details/40921209
作者:nineheadedbird